风光水多能互补发电系统日内时间尺度运行特性分析

叶 林, 屈晓旭， 么艳香, 张节潭， 王跃峰， 黄越辉， 王伟胜

(1. 中国农业大学信息与电气工程学院， 北京市 100083； 2. 青海省光伏发电并网技术重点实验室(国网青海省电力有限公司电力科学研究院)， 青海省西宁市 810008； 3. 新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)， 北京市 100192)

0 引言

化石能源的日益衰竭，促使人们高度关注太阳能、风能、水能等可再生能源[1-2],高比例可再生能源并网成为电力系统的发展方向[3]。然而，风力发电和光伏发电都具有较强的随机性、波动性和间歇性，大规模风电和光电并网使得电力系统的安全稳定运行面临严峻考验[4-6]。而水电作为规模大、调节性能良好的电源，可以有效平抑风力发电和光伏发电波动，提高电网对其的消纳能力。因此，对风光水互补发电系统的运行特性进行准确分析显得尤为重要。

现有研究大多集中在风、光、水等单独发电系统的运行特性，或风光、风水等两种能源互补发电系统的建模仿真、优化配置、控制策略等方面，针对风光水多能互补发电系统有功功率输出特性的研究则相对较少[7-10]。风、光、水的有功功率输出在年内和日内时间尺度均具有一定的互补性，但文献[11]对其互补特性只是初步探索，分析不够深入。目前，国内外普遍采用皮尔逊相关系数来衡量不同电源间的相关性[12-13]，但相关系数对信号局部变化相似度的描述并不显著。一致性指标和互补性指标[14]虽更突出考察不同信号动态变化差异程度，但也仅限于描述某两个信号间的互补能力,具有一定的局限性。互补率和平滑度[15]可以评估风、光的自然互补特性和风、光、储的人工互补特性，但计算较为复杂，且不易理解。

在电力系统的评价指标体系方面，对风、光单一发电系统的评价指标体系已有研究[16-18]，但各体系包含的指标大多具有针对性，并不适用于多能互补发电系统。目前，针对多种能源互补特性的指标评价体系尚不完善，标准参差不一。少数涉及多能互补发电系统评价体系的文献则主要关注了风光储互补发电系统的发电特性[19-21]。文献[22]利用弃光率、火电负荷率、上网收益等指标，从侧面评价光水互补系统的运行特性，而对于各电源间的互补特性，仅以功率波动大小进行衡量，计算方法具有一定的局限性。各种发电系统的评价指标种类繁多，无法综合反映多种能源互补发电系统的输出功率特性。

基于此，本文首先针对风光水发电互补特性评价指标进行深入研究，对多种评价指标进行了整理和分类，从分系统与联合发电系统评价两个方面入手，并利用互补系数将两者结合，构建了适用于风光水互补发电系统的评价指标框架。最后以中国西部某省为例，选取指标框架中典型指标计算分析，研究表明，风光水在日内时间尺度存在较强的互补性。

本文所提出的风光水互补发电评价指标研究框架弥补了以往风光水评价指标体系的不足，为风、光、火、水、气等多种能源互补发电运行特性的评价研究提供了参考。

1 风光水互补发电评价指标研究框架

风光水互补发电系统集风力发电、光伏发电与水力发电为一体，既是一个整体，各部分也可以看做独立的发电单元，即分系统。因此首先需要通过分系统的指标评判其运行特性，再从风光水互补发电系统整体对电网的并网运行进行指标分析。根据分系统与联合发电系统的运行特点及所需响应指标的侧重点不同，本文拟将风光水互补发电系统的评价指标分为分系统评价指标和联合发电系统评价指标两大类，并将评价多个分系统互补性能的评价指标作为连接分系统与联合发电系统的桥梁，使两者有机结合。对于分系统评价指标，本文从其稳定性、分布特性和功率预测误差三个方面对分系统指标进行讨论；对于联合发电系统评价指标，为了实现多能互补有功功率的平滑输出、削峰填谷、计划跟踪和调峰调频等目标，本文拟从多能互补系统的可靠性、负荷匹配度和有功功率控制效果三个方面分析，定量评估风光水互补发电系统的互补特性。

指标框架的构建与指标的选取均需遵循一定的原则。在指标的选取过程中，一方面要保证指标体系的全面性和代表性，涵盖评价对象的各方面特性；另一方面还要保证选取指标的目的性，使其均能客观反映评价对象关于评价目标的特性。基于以上原则，本文所构建的风光水互补发电运行特性的评价指标框架如图1所示。

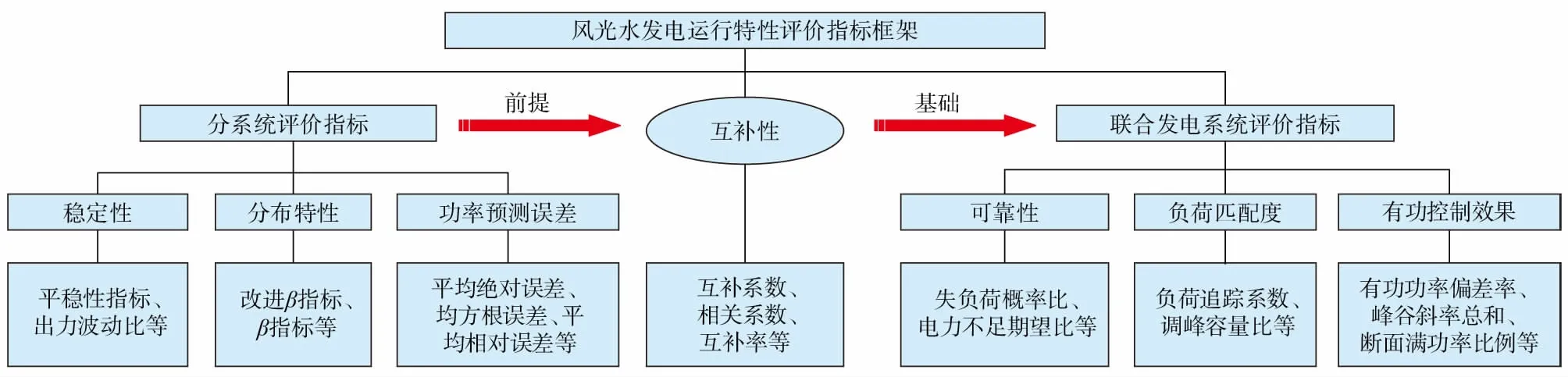
图1 风光水发电运行特性评价指标框架Fig.1 Evaluation index framework for operation characteristics of wind-solar-hydro power system

2 风光水运行特性评价指标

2.1 分系统评价指标

2.1.1平稳性

高比例可再生能源，如风、光等接入大系统后将对电网造成负面影响，成为电力系统不确定性的主要来源，给电力系统的安全稳定和经济运行带来巨大的挑战，因此，有必要对单体系统的输出功率进行平稳性评估，防止其并网造成安全隐患。为分析发电系统输出功率的平稳性，引入考察时间尺度内的功率平稳性指标IS[14]来量化评估功率波动程度:

(1)

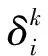
平稳性指标的大小反映了在考察时间尺度内功率波动的程度：数值越小，说明功率波动越小，平稳性越好；反之，功率波动越剧烈，则平稳性越差。

2.1.2概率分布特性

风力发电和光伏发电均具有随机性和间歇性，因此其输出功率的分布特性常用累计概率曲线表示，用来描述可再生能源输出功率的均衡情况。文献[23]定义的改进β指标可用于描述输出功率：

(2)

式中：S1为累积概率曲线与输出功率标幺值在β到1之间围成的面积；S2为累积概率曲线与输出功率标幺值在0到β之间围成的面积。

2.1.3功率预测误差

利用功率预测技术可以减轻新能源功率输出的波动性对电力系统调度的不利影响。目前风力发电和光伏发电均装有相应的功率预测系统，但是由于风能和太阳能资源的间歇性和随机性较强，其预测误差较大，短期预测精度有待提高[24-25]，因此可以利用功率预测误差对预测系统进行对比评价，了解预测系统的运行情况。本文基于风力发电场和光伏电站实时数据(包括实际功率和预测功率)，对风力发电、光伏发电和风光水互补发电的实际功率与预测功率进行分析，对比各发电系统功率预测结果，采用平均绝对误差(MAE)和均方根误差(RMSE)对各发电系统功率预测结果进行分析。各项误差指标的值越小，则预测精度越高。

2.2 互补性评价指标

互补性评估的前提是进行分系统运行特性的评估，若分系统的运行指标尚未达到运行标准，那么进行互补性的评估则失去意义。互补性指标也是联合发电系统运行特性评估的基础，其可以对多种能源互补的程度进行初步的判断。互补性越高，则越有利于联合发电系统的并网运行。

对于风力发电系统，为量化两个风电功率信号的互补能力，文献[14]定义了互补性指标来定量评估不同功率变化量相互抵消的程度，本文在其基础上加以改进，定义了适用于多种能源互补发电系统的互补特性评估指标——互补系数IC，来量化评估多个功率信号叠加后的功率波动情况。令

(3)

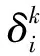
考察某时间尺度内量化评估多种能源系统发电功率的互补程度，定义互补系数：

(4)

互补系数的大小反映了各功率信号互补的程度，IC越接近于0，说明在考察时间尺度内各信号变化量相互抵消得越多,互补性越强；反之，IC越大，信号变化量相互抵消得越少，则其互补性越弱。

2.3 联合发电系统评价指标

2.3.1可靠性

现阶段常用的电力系统可靠性指标主要有确定性和概率性两种，前者只是某一过程的极值，后者则可以反映整个模拟过程的特性，现阶段已逐步取代前者[26]。多种能源互补发电系统主要是通过改变系统总输出功率来影响系统可靠性。可再生能源大都具有很强的随机性和波动性，有功功率输出往往难以满足负荷的要求。失负荷概率比和电量不足期望比分别从电力角度和电量角度描述了多种能源互补后对系统可靠性的影响。

1)失负荷概率比[27](电力不足时间概率比)：多种能源互补后的电力不足期望时间与单一发电系统的电力不足期望时间之和的比值。公式如下：

(5)

式中：tLOLP为多种能源互补后的电力不足期望时间；tLOLPi为第i种单一发电系统的电力不足期望时间。ρ值的范围为0～1,ρ值越小，表明互补性越好。

2)电量不足期望比[27]：多种能源互补后的电量不足期望值与单一发电系统电量不足期望值之和的比值。公式如下：

(6)

式中：λEENS为多种能源互补后的电量不足期望值；λEENSi为第i种单一发电系统的电力不足期望值。k值的范围为0～1，k值越小，表明互补性越好。

2.3.2负荷匹配度

1)负荷追踪系数

多能互补是将各种发电能源进行优化组合配置，使各种信号叠加后更好地跟随负荷变化，从而使系统安全稳定运行，因此有必要引入负荷追踪系数用来衡量负荷的匹配度。文献[14]定义了一致性指标来定量评估各个信号的接近程度。因此，为了分析风力发电、光伏发电等多种可再生能源发电系统对负荷的影响，本文在一致性指标基础上进行了改进，定义负荷追踪系数IT，来量化评估多种电源跟踪负荷的特性。假设

(7)

令

(8)

则tk可以简化为:

(9)

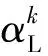
考察某时间尺度内多种电源功率与负荷功率变化不一致程度，定义负荷追踪系数：

(10)

IT越接近于0，说明多种能源互补发电功率与负荷功率在考察时间尺度内的变化特性越一致，发电系统的输出功率对负荷的跟踪性越好；反之，IT越大，说明发电功率与负荷在考察时间尺度内的变化特性越不一致，跟踪性越差。

2)调峰容量比[27]

波动性和随机性是风、光等可再生能源最典型的自然特征，需配置合理的调峰容量，否则当出现风力减小或光照幅度下降导致发电不足，而此时系统调峰容量不能有效满足负荷时，会对系统频率产生一定的影响。因此，引入调峰容量比作为调峰方面的核心指标，即能源互补后的系统需求调峰容量与单一发电系统需求调峰容量最大值之比，用来定量评估多能互补后最大可调功率输出与最小技术功率输出之差的改善程度。公式如下：

(11)

式中：Ereg为多种能源互补后需要的调峰容量；Eregi为第i种单一电源需要的调峰容量。λ取值范围为0～1，λ值越小，表明调峰容量互补性越高。

2.3.3有功控制效果

对于多能互补发电系统，为了衡量其整体发电功率输出的控制效果，引入有功功率偏差率ΔP[17]来衡量其总输出功率相对于计划出力的偏移程度：

(12)

式中：Ptotal为多能互补发电系统的实际功率输出值；Pref为功率输出的计划值。ΔP越小，表明功率输出对计划曲线的跟踪性越好，有功控制效果越好。无功功率在本文中视为可以随系统进行调节而达到平衡，因此，本文不对无功功率做过多讨论。

3 算例分析

本文数据来源于中国西部某省电力公司，以某地区电网实际风电场(50 MW)、光伏发电站(20 MW)和水力发电站(20 MW)为例进行分析。该地区系统最大负荷水平为1 201.15 MW。由于在实际运行中存在弃风弃光现象，风电场和光伏电场所处的环境变化多端，再加上监测系统存在随机误差和系统误差等对风电场和光伏电场运行监测数据产生一定的影响，从而导致一些异常数据的产生。这些异常数据的存在会对功率特性分析产生较大影响。因此，本文首先借鉴文献[28-29]的方法，对原始数据进行预处理和归一化，提高数据质量。

为了避免偶然性，本文随机选取该省风电场、光伏电站和水力发电站某年4个历史日的采样点进行分析，以平稳性指标、误差指标和负荷追踪系数为例，对风光水互补发电系统的日内时间尺度的功率特性进行分析。

3.1 基于平稳性指标的平稳性分析

对于风、光、水分系统,以平稳性指标为例进行分析。分别计算风力发电、光伏发电、水力发电的平稳性指标，再将风光水发电功率耦合，将风光水互补发电系统看成一个大的系统，并计算其平稳性指标，计算结果如表1所示。

由表1可见，风力发电和光伏发电功率的平稳性指标偏大，尤其是在12月30日。由此可知,风力发电和光伏发电功率波动性较水力发电大。这是由光伏发电昼发夜停和风力发电具有较强的随机性和波动性造成的。水力发电站的发电量受流经水电机组的水流影响，而短时间内水流基本不会发生很大变化，且同时受来水装置的控制，所以短期内水电站的功率输出比较平稳。由表1可见，其平稳性指标最小，因此功率波动较小。风光互补发电和风光水互补发电功率平稳性指标均小于风电单独出力和光伏单独输出的平稳性指标，由此可得，风光和风光水互补发电功率平稳性较高，风光互补可以平抑风力发电的波动性，而水力发电具有平抑风力发电和光伏发电功率波动的能力，而这也与事实相符。

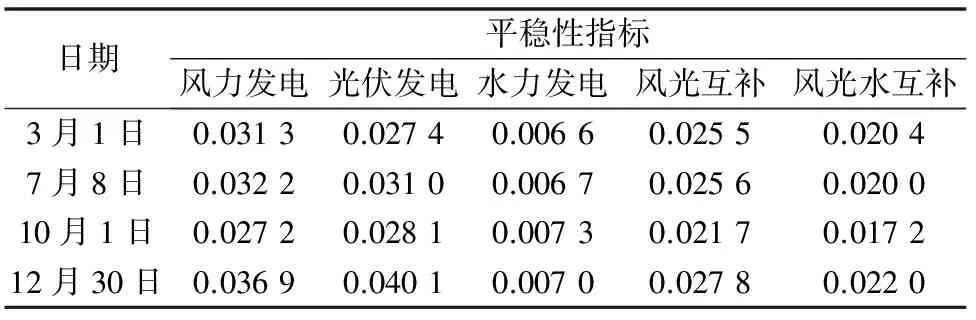
表1 风光水互补发电系统平稳性指标计算结果Table 1 Results of stability index of hybrid wind-solar-hydro power generation system

统计各发电功率平稳性指标的概率分布及累积概率。风、光、水单独发电和风光水互补发电的功率平稳性指标概率分布和累积概率分布见附录A图A1。由其统计结果可知，水力发电的功率平稳性指标主要集中在0处，说明水力发电功率输出最平稳。此处的光伏发电功率平稳性指标概率也较高，但这并不能说明光伏发电功率平稳性高，而是由于光伏发电昼发夜停，在夜间光伏功率输出为0，因此出现了较高的概率。相比风力发电功率和光伏发电功率，风光水互补发电功率概率分布相对集中，这说明其功率平稳性较风、光单独发电功率平稳性高。

3.2 基于误差指标的功率预测误差分析

因水电站的功率输出与降水量、河流水流量、水库库容及水轮机机组特性等因素相关，而短时间内这些因素基本不会发生很大变化，所以短期内水电站的功率输出比较平稳，可以认为其预测值与实际值基本一致。

以3月1日07：00—19：00时间尺度内的样本对风力发电、光伏发电和风光水互补发电功率预测进行分析，分别计算风、光单独发电功率和风光水互补发电功率预测误差。该日内的风力发电、光伏发电和风光水互补发电实际发电功率和功率预测值见附录A图A2(a)(b)(c)，07：00—19：00时间尺度内风力发电、光伏发电和风光水互补发电功率预测相对误差的概率分布情况见附录A图A2(d)。可知，风光水互补发电功率预测的相对误差较风力发电和光伏发电功率预测分布更为集中。其平均绝对误差和均方根误差的比较结果如表2所示。

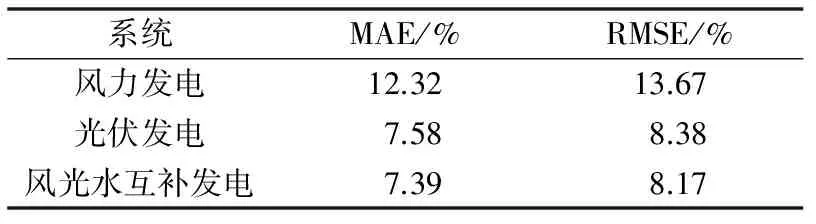
表2 风光水互补发电系统功率预测误差结果Table 2 Results of power prediction error of hydrid wind-solar-hydro power generation system

由表2可以看出，风光水互补发电功率预测的MAE和RMSE最小，精度最高。可以说明，风光水互补发电功率预测能有效地减小风力发电和光伏发电的功率预测误差值，将使系统对风力发电和光伏发电的调度和优化运行起到重要作用。

3.3 基于互补系数的互补特性分析

对于风光水互补特性，分别从两两互补和三者互补的角度对其互补系数进行分析。

由表3可见，所选取的日期中风光水互补发电系统的互补系数均最低，说明风力发电、光伏发电和水力发电合成的功率输出的互补性最好。风力发电系统和光伏发电系统的互补系数均为最高，说明风光的互补性最低，水电作为规模大、调节性能良好的电源，可以在一定程度上对风光互补起到平滑作用。

表3 风光水互补发电系统互补系数结果Table 3 Results of complementary index of hybrid wind-solar-hydro power generation system

风光水互补发电系统功率曲线见附录A图A3。可以看出，每日的06：00以前和18：30以后，风光互补和风光水互补发电归一化功率均低于风力发电，这是由于光伏发电昼发夜停所致。而在每日的06：00—18：00之间，无论是风光互补发电还是风光水互补发电，均可以较好地平抑风力发电的波动性，尤其在7月8日的中午最为明显。其中，风光水互补发电的功率输出又明显好于风光互补，这也与互补系数的计算结果相符。

风光互补、光水互补、风水互补和风光水互补发电系统的互补系数指标的概率统计和累积概率统计分布见附录A图A4。可知，虽然风光水互补发电系统的互补系数最低，但在概率统计上考虑，其并不能说明风光水互补发电总是最佳的。显然，在7月8日，风光水耦合输出的互补系数概率分布主要集中在0～0.05之间，而在其他日期，其概率分布比较分散，与其他的互补形式相比，没有明显的优势。例如：在10月1日，风光水互补发电系统的互补系数累积概率曲线与风水互补发电系统的互补系数累积概率曲线接近。因此，除了互补系数，还要利用联合发电系统指标对其运行特性进行进一步分析。

3.4 基于负荷追踪系数的负荷匹配度分析

该地区春、夏、秋、冬四季典型日风力发电、光伏发电和水力发电功率曲线和负荷功率曲线见附录A图A5。分别计算风力发电、光伏发电、水力发电系统单独运行的负荷跟踪情况和风光水互补发电系统的负荷跟踪情况，并统计各种情况下负荷追踪系数的概率分布和累积概率。计算结果如表4所示。

表4 风光水互补发电系统负荷追踪系数结果Table 4 Results of load tracking index of hybrid wind-solar-hydro power generation system

由表4可见，水力发电的负荷追踪系数最低，说明其跟踪负荷能力最强，其中7月8日的水电负荷追踪系数达到水电中的最低值，这说明水力发电高峰时期，对负荷的跟踪能力也最强。风力发电和光伏发电负荷追踪系数较大，对负荷的跟踪能力较差。这是由于单独的风力发电和光伏发电并网中，白天光伏发电一般呈正调峰，但在夜间，负荷高峰期光伏没有功率输出；而风力发电具有较强的随机波动性，且有一定的反调峰性[30]，因此，风力发电和光伏发电对负荷的跟踪能力较差。与单独的风力发电和光伏发电相比，风光水互补发电的功率输出能对负荷保持较好的跟踪，从而减小对系统的冲击。

风力发电、光伏发电、水力发电和风光水互补发电功率的负荷追踪系数概率统计和累积概率分布见附录A图A6。可知，7月8日水力发电负荷追踪系数概率分布主要集中在0～0.05，其概率累积在0.1处便达到了100%。对于其他日期，水力发电负荷追踪系数概率分布也比较集中。而风力发电和光伏发电的负荷追踪系数概率分布比较分散。可以这么认为，水力发电出力负荷追踪指标概率曲线对风力发电和光伏发电出力负荷追踪指标概率曲线起到调整作用，使二者最终达到相对集中的风光水互补发电负荷追踪指标概率曲线。

4 结语

本文建立了从不同角度对风光水发电运行特性进行评价的指标框架，并对重点指标进行详细说明和完善。对比分析风、光、水单一发电系统和风光、风水、光水、风光水互补发电系统的平稳性、互补性、负荷跟踪特性和功率预测误差指标，得出以下结论。

1)以功率平稳性指标评价发电系统功率的平稳性，水力发电具有平抑风力发电和光伏发电波动性的特点，使得风光水互补发电功率波动减小，增强功率平稳性。

2)风光水互补发电功率预测的预测误差较单独的风力发电功率预测和光伏发电功率预测误差更小，且误差分布更集中。

3)风水互补和光水互补的性能在不同日期呈现出不同的优劣程度，说明其互补特性可能与季节相关，后续可开展深入研究。

4)风光水互补发电系统的互补系数概率分布大都较分散，与其他耦合形式相比，没有明显的优势。因此，该指标可以根据需求指导电源规划和配置。

5)水力发电的负荷追踪系数概率分布比较集中，其负荷跟踪特性最好。在水力发电的调节作用下，风光水互补发电功率负荷跟踪能力较单独的风力发电和光伏发电有一定提升。

本文对风力发电、光伏发电、水力发电和风光水互补发电功率特性进行量化评估，评估方法和结果能够为多种异质能源电力系统的运行调度提供参考依据。但在分系统评价指标和互补性评价指标对联合发电系统评价指标的影响程度方面，本文存在一定的局限性，后续可开展相关量化评估研究工作。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] PAPAEFTHYMIOU G, DRAGOON K. Towards 100% renewable energy systems: uncapping power system flexibility[J]. Energy Policy, 2016, 92: 69-82.

[2] 贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-206.DOI:10.7500/AEPS20141009011.

JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of Electric Power Systems, 2015, 39(7): 198-206. DOI: 10.7500/AEPS20141009011.

[3] 鲁宗相,李海波,乔颖.高比例可再生能源并网的电力系统灵活性评价与平衡机理[J].中国电机工程学报,2017,37(1):9-20.

LU Zongxiang, LI Haibo, QIAO Ying. Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity[J]. Proceedings of the CSEE, 2017, 37(1): 9-20.

[4] PETRAKOPOULOU F, ROBINSON A, LOIZIDOU M. Simulation and analysis of a stand-alone solar-wind and pumped-storage hydropower plant[J]. Energy, 2016, 96(2): 676-683.

[5] 黎嘉明,艾小猛,文劲宇,等.光伏发电功率持续时间特性的概率分布定量分析[J].电力系统自动化,2017,41(6):30-36.DOI:10.7500/AEPS20160604002.

LI Jiaming, AI Xiaomeng, WEN Jinyu, et al. Quantitative analysis of probability distribution for duration time characteristic of photovoltaic power[J]. Automation of Electric Power Systems, 2017, 41(6): 30-36. DOI: 10.7500/AEPS20160604002.

[6] TAN Z, NGAN H W, WU Y, et al. Potential and policy issues for sustainable development of wind power in China[J]. Journal of Modern Power Systems and Clean Energy, 2013, 1(3): 204-215.

[7] 夏永洪,吴虹剑,辛建波,等.考虑风/光/水/储多源互补特性的微网经济运行评价方法[J].电力自动化设备,2017,37(7):63-69.

XIA Yonghong, WU Hongjian, XIN Jianbo, et al. Evaluation of economic operation for microgrid with complementary DGs and energy storage[J]. Electric Power Automation Equipment, 2017, 37(7): 63-69.

[8] SONG D, YANG J, CAI Z, et al. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines[J]. Applied Energy, 2017, 190: 670-685.

[9] MONFORTI F, HULD T, BDIS K, et al. Assessing complementarity of wind and solar resources for energy production in Italy: a Monte Carlo approach[J]. Renewable Energy, 2014, 63(1): 576-586.

[10] ANJOS P S D, SILVA A S A D, STOIB, et al. Long-term correlations and cross-correlations in wind speed and solar radiation temporal series from Fernando de Noronha Island, Brazil[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 424: 90-96.

[11] 朱燕梅,邹祖建,黄炜斌,等.金沙江上游典型电站水光风互补运行研究[J].水力发电学报,2017,36(4):78-85.

ZHU Yanmei, ZOU Zujian, HUANG Weibin, et al. Complementary operation of water, wind and solar power for typical power stations on upper Jinsha River[J]. Journal of Hydroelectric Engineering, 2017, 36(4): 78-85.

[12] SILVA A R, PIMENTA F M, ASSIREU A T, et al. Complementarity of Brazil’s hydro and offshore wind power[J]. Renewable and Sustainable Energy Reviews, 2016, 56: 413-427.

[14] 曲直,于继来.风电功率变化的一致性和互补性量化评估[J].电网技术,2013,37(2):507-513.

QU Zhi, YU Jilai. Quantitative evaluation on consistency and complementarity of wind power variability[J]. Power System Technology, 2013, 37(2): 507-513.

[15] 李洪美,罗建裕,万秋兰.含间歇性电源的发电资源互补优化研究[J].电力系统保护与控制,2013,41(9):34-39.

LI Hongmei, LUO Jianyu, WAN Qiulan. Manual complementariness optimization of electrical source involving intermittent power[J]. Power System Protection and Control, 2013, 41(9): 34-39.

[16] 李剑楠,乔颖,鲁宗相,等.多时空尺度风电统计特性评价指标体系及其应用[J].中国电机工程学报,2013,33(13):53-61.

LI Jiannan, QIAO Ying, LU Zongxiang, et al. An evaluation index system for wind power statistical characteristics in multiple spatial and temporal scales and its application[J]. Proceedings of the CSEE, 2013, 33(13): 53-61.

[17] 王震,鲁宗相,段晓波,等.分布式光伏发电系统的可靠性模型及指标体系[J].电力系统自动化,2011,35(15):18-24.

WANG Zhen, LU Zongxiang, DUAN Xiaobo, et al. Reliability model and indices of distributed photovoltaic power system[J]. Automation of Electric Power Systems, 2011, 35(15): 18-24.

[18] 陈力,胡钋,卫敬宜,等.一种新的光伏并网评价体系[J].电力系统保护与控制,2017,45(2):105-110.

CHEN Li, HU Po, WEI Jingyi, et al. A new evaluation system of grid-integrated PV generation[J]. Power System Protection and Control, 2017, 45(2): 105-110.

[19] 张蕊.风光储联合发电系统评价指标体系研究[D].北京:华北电力大学,2014.

[20] 赵宇思.风光储联合发电系统运行特性评价研究[D].北京:华北电力大学,2016.

[21] YAO L, YANG B, CUI H, et al. Challenges and progresses of energy storage technology and its application in power systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 519-528.

[22] 田旭,张祥成,白左霞,等.青海省水电与光伏互补特性分析与效果评价[J].电力建设,2015,36(10):67-72.

TIAN Xu, ZHANG Xiangcheng, BAI Zuoxia, et al. Characteristic analysis and effect evaluation of synergy between hydropower and photovoltaic power in Qinghai Province[J]. Electric Power Construction, 2015, 36(10): 67-72.

[23] 徐乾耀,康重庆,张宁,等.海上风电出力特性及其消纳问题探讨[J].电力系统自动化,2011,35(22):54-59.

XU Qianyao, KANG Chongqing, ZHANG Ning, et al. A discussion on offshore wind power output characteristics and its accommodation[J]. Automation of Electric Power Systems, 2011, 35(22): 54-59.

[24] PETRAKOPOULOU F, ROBINSON A, LOIZIDOU M. Simulation and analysis of a stand-alone solar-wind and pumped-storage hydropower plant[J]. Energy, 2016, 96(2): 676-683.

[25] GOLOV N, RÖNNBCK L. Big data normalization for massively parallel processing databases[C]// International Conference on Conceptual Modeling, October 19-22, 2015, Stockholm, Sweden: 154-163.

[26] 张培.基于可信容量的风光互补发电系统特性研究[D].济南:山东大学,2016.

[27] 钟跃.能源互补评价指标及其应用[D].长沙:湖南大学,2013.

[28] LYDIA M, KUMAR S S, SELVAKUMAR A I, et al. A comprehensive review on wind turbine power curve modeling techniques[J]. Renewable and Sustainable Energy Reviews, 2014, 30(2): 452-460.

[29] BENMOUIZA K, TADJ M, CHEKNANE A. Classification of hourly solar radiation using fuzzy C-means algorithm for optimal stand-alone PV system sizing[J]. International Journal of Electrical Power & Energy Systems, 2016, 82: 233-241.

[30] DE JONG P, SNCHEZ A S, ESQUERRE K, et al. Solar and wind energy production in relation to the electricity load curve and hydroelectricity in the northeast region of Brazil[J]. Renewable and Sustainable Energy Reviews, 2013, 23: 526-535.