基于Stackelberg博弈模型的综合能源系统均衡交互策略

吴利兰, 荆朝霞, 吴青华, 邓 珊

(华南理工大学电力学院, 广东省广州市 510641)

0 引言

基于天然气的分布式能源站(distributed energy station,DES)[1-2],可以为用户提供冷、热、电多种能源,用能效率可达80%以上,是现今综合能源系统(integrated energy system,IES)中最具商业前景的一种运营模式[3-4]。中国国家能源局于2017年3月发布了《关于开展分布式发电市场化交易试点的通知》,鼓励发展多能互补方式,并逐步开放市场。随着能源种类和市场参与者数量的增加,IES的优化运行和参与者的交易策略将越来越复杂[5]。

在IES的运行优化方面,文献[6]考虑了储能,采用场景分析法对可再生能源建模,以总运行成本为目标求解包含多个DES的IES内各单元的最优出力。文献[7-9]建立了微网中含有多个DES的调度优化模型,并且考虑了分时电价并采用混合整数线性规划方法进行求解。以上文献均分析了多个区域的DES互联的协同优化问题,但是都只考虑了DES的运行成本,而未讨论DES在市场环境中的收益和定价问题。

随着能源互联网[10-11]的发展,DES可以向多个用户供应能源,实现能源互联。在开放的市场模式下,DES要如何设定生产策略和如何制定冷热电的价格来实现盈利最大化,是当下关注的热点,但是目前鲜有文献涉及这方面的研究。博弈方法可求解理性市场参与者的最优策略。博弈均衡解将对能源价格的制定和DES的规划和运行具有重要指导意义。因此,为了分析DES在市场环境中的最优策略,关于多种能源生产和交易的均衡交互策略值得研究。

在与IES相关的博弈方面,文献[12-14]建立了静态非合作博弈模型,用于求解天然气网和电网公司与DES之间的均衡交互量,并分析了DES对电网的调峰作用。文献[15]通过建立势博弈模型来分析多个DES对电网和天然气网的耦合需求响应。然而上述文献都是建立了只考虑了能源交易量,而把能源价格简单处理为产量函数的静态博弈模型,并且都只关注到DES与电网和天然气网的交互,而把用户需求看作定值,没有涉及与用户交互和热电能源的定价问题。

考虑用户的需求响应时,DES先决定能源价格,能源用户(EU)根据价格决策需求量[16-17],两者存在决策的先后顺序,根据此特征,本文采用具有主从复合结构的Stackelberg博弈模型来分析DES和EU之间的交互[18]。

至今,已有许多研究提出了不同的Stackelberg模型来分析电能供给者和消费者之间的交互。文献[19-20]创建了一个多主多从Stackelberg博弈模型来分析多个售电公司和多个用户之间的均衡交易策略。文献[21-22]提出了用于分析多个微网之间针对富余能源的均衡交互策略的多主多从Stackelberg博弈模型。然而以上与能源交易有关的动态博弈模型都只关注到电能的交易。目前,关于IES中多种能源交易方面的动态博弈方法的研究,仍然是个空缺。

本文将重点关注IES中多个DES和EU之间的均衡定价和定量问题,通过建立多主多从的Stackelberg博弈模型,求解出各个参与者理性追求各自目标时的均衡交互策略。首先,建立了DES和EU的数学模型,分析了双方的目标函数特性。此外,通过分析所提的博弈模型性质,证明了所提能源交易博弈存在唯一的Stackelberg均衡解,并推导出均衡解的闭式表达式。最后,提出了仅使用有限信息的分布式迭代算法来求解出该博弈的均衡解。

1 IES模型

如图1所示,本文研究的IES包含K个DES(T={1,2,…,K})和N个EU(V={1,2,…,N})。本模型中,DES通过消耗天然气向EU提供电能和热能,假设EU的电需求和热需求都由DES提供。作为能源供应商,DES追求最大化各自的收益,他们之间形成相互竞争。需要强调的是,本文研究的多种能交易模型是建立在完全竞争市场的假设之上的,即所有的生产者都会以统一的市场价格与消费者进行交易。本节将仔细讨论IES中DES和EU的数学模型。

图1 IES示意图Fig.1 Schematic diagram of IES

1.1 DES模型

图2给出了DES的简化图,DES使用各种能源生产和转换设备,通过输入天然气生产出电能和热能供应给用户。其中的能源生产和转换设备包括燃气轮机(gas turbine,GT)、余热锅炉(heat recovery steam generator,HRSG)、蒸汽轮机(steam turbine,ST)和热转换机(heat exchanger,HE)。DESk的能量转换方程为:

(1)

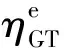
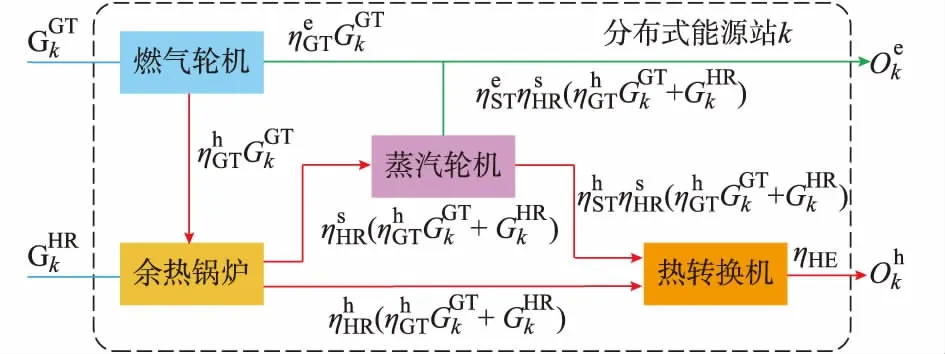
图2 热电联供DES示意图Fig.2 Schematic diagram of combined heat and power DES

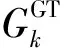
(2)

(3)

(4)

(5)

1.2 EU模型

在微观经济学中,效用函数常被用于量化消费者在消费某一商品时获得的满意程度。本文定义EUn的效用为该用户购买电能和热能所获得的满意度的总和。本文采用常用的二次效用函数来表示EUn消费能源获得的效用[19-20,26],其表达式为:

(6)

在能源交易中,每个EU根据单位电价和热价决定电能和热能的需求量,目标为最大化消费者剩余。消费者剩余即效用与购买能源的成本之差。因此,EUn的最优需求响应问题可以描述为[19-20]:

(7)

(8)

式中:Wn为EUn的消费者剩余函数。

(9)

2 IES中的Stackelberg博弈模型

本文建立了多主多从的Stackelberg博弈模型来分析IES中DES和EU之间的均衡多能交易问题。Stackelberg博弈是一种双层的主从复合非合作博弈方法[18],在博弈中,DES作为领导者各自以最大化收益的目标来制定单位电价和单位热价,EU作为跟随者以最大化消费者剩余为目标,根据领导者的行为决定其能源需求量。本文所提的IES中的Stackelberg博弈模型的标准型表示如下:

n∈V,k∈T,n∈V,k∈T

(10)

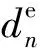
当所有跟随者对领导者策略作出最优响应并且领导者接受了这个响应时,博弈达到Stackelberg均衡[19-20,26]。令ρ*表示所有DES的均衡策略向量,δ*表示所有EU的最优响应策略向量。若以下条件成立,则(ρ*,δ*)为所提能源交易博弈的Stackelberg均衡。

(11)

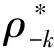
2.1 供给侧分析

(12)

式中:μk,1和μk,2为Lagrange乘子,∀k∈T。

式(12)的互补松弛条件为:

(13)

把式(1)和式(9)代入式(12),可以得到一阶最优条件如下:

(14)

(15)

(16)

(17)

(1+αe)(Be-Aepe)=0

(18)

(1+αh)(Bh-Ahph)=0

(19)

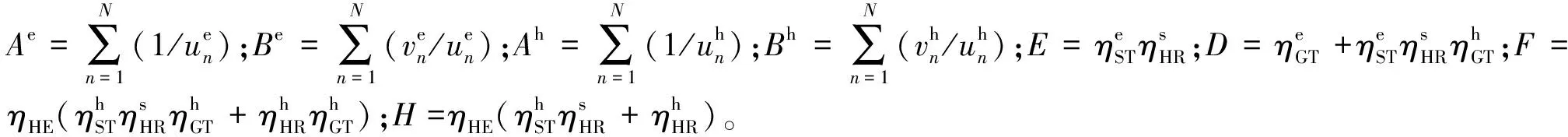
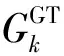
(20)

(21)

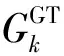
(22)

把式(21)代入式(22),可以得到:

(23)

式中:I=BeD/Ae+BhF/Ah;J=BeE/Ae+BhH/Ah。

通过观察,可以把式(23)写成矩阵形式:

(24)

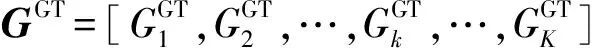
(25)

因此,当(Y2-XZ)≠0时,可以得到式(24)的解为:

(26)

式中:R-1=R*/|R|,|R|=1+K。

(27)

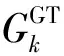
(28)

式(28)中,DESk的最优运行方式只与其运行参数和EU的需求特性有关。把式(28)代入式(21)中,可以得到单位电价和单位热价的闭式表达式如下:

(29)

2.2 DES的定价博弈

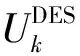
结论1:DES之间的非合作定价博弈是一个超模博弈。

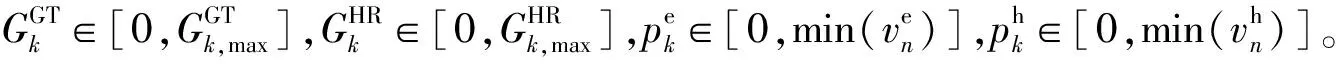
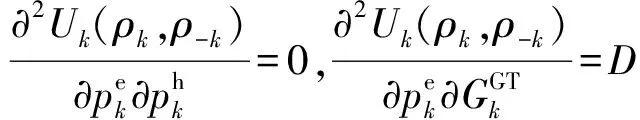
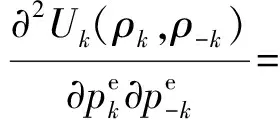
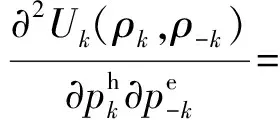
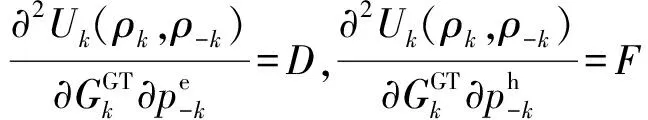
上述公式表明,DESk的目标函数对其他DES的策略变量的交叉偏导都满足非负条件。因此,DES之间的非合作定价博弈是一个超模博弈。

根据超模博弈的性质,DES之间的非合作定价博弈存在纯策略Nash均衡解[31-33]。另外,在2.1节中推导出了DES策略变量的闭式表达式,这说明DES策略集存在唯一非负解。由此证明了DES之间的非合作定价博弈的Nash均衡解是唯一的。

2.3 Stackelberg博弈均衡的唯一性

结论2:DES与EU之间的能源交易博弈存在唯一的Stackelberg均衡解。

3 分布式算法

集中优化方法需要知道参与者的目标函数的确切信息,然而现实中交易双方不会愿意向竞争对手透露他们各自的目标函数[34]。为了保护商业信息,本节提出了一种求解DES与EU之间能源交易博弈Stackelberg均衡的分布式算法,该算法不需要交易双方透露目标函数信息。所提分布式算法的伪代码如下。

记迭代次数i=0;

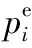
while (the termination conditions are not met) do

for (DESkk=1,2,…,K) do

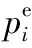
end for

for (EUnn=1,2,…,N) do

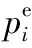
end for

break

else

更新单位电价和单位热价并转向下一次迭代;

end if

i=i+1;

end while

(30)

为了提高算法的收敛速度,采用与当前迭代次数i有关的动态速度调整参数[26],如下:

(31)

式中:λe,μe,λh和μh为常数。

4 算例分析

本节将通过算例分析来验证所提的Stackelberg博弈模型的有效性和分布式算法的快速收敛性。此外,还将分析DES的成本参数、EU的消费偏好参数及DES的数量和EU的数量对博弈均衡解的影响。

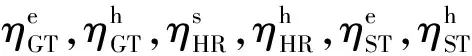
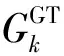
图3 迭代初始值时的分布式算法收敛图Fig.3 Convergence diagram of distributed algorithm when =0.423 8,=0.017 9

图4 迭代初始值时的分布式算法收敛图Fig.4 Convergence diagram of distributed algorithm when =35.157 9,=50.845 6

4.1 DES的成本参数对博弈均衡解的影响

4.2 EU的偏好参数对博弈均衡解的影响

4.3 DES的数量对博弈均衡解的影响

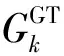
4.4 EU的数量对博弈均衡解的影响

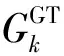
5 结语

本文建立了用于分析IES中,多个DES和EU的能源交易均衡问题的多主多从Stackelberg博弈模型。博弈模型考虑了每个DES的收益和每个EU的消费者剩余。通过分析,证明了领导者DES之间的非合作定价博弈满足超模博弈性质,存在纯策略Nash均衡。同时,证明了DES和EU之间的能源交易博弈存在唯一的Stackelberg均衡。此外,本文推导了DES和EU的Stackelberg均衡解的闭式表达式。最后,提出了一个仅使用有限信息来求解所提博弈模型的Stackelberg均衡解的分布式算法。

算例分析验证了所提的分布式算法具有快速收敛性,其结果与闭式表达式的结果吻合。此外,分别研究了DES的成本参数、EU的消费偏好参数、DES的数量和EU的数量对市场价格的形成和每个市场参与者在博弈中的行为所造成的影响。

在未来的多种能源交易市场中,本文所提的博弈模型有助于分析市场参与者的均衡策略,或者应用于制定中长期交易机制或合同。但是本文考虑的用户模型不够全面,能源类型不够丰富,后续的研究,将拓展能源供应商和消费者的类型和能源的种类,探究更为复杂的多种能源交易问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] JIANG X S, JING Z X, LI Y Z, et al. Modelling and operation optimization of an integrated energy based direct district water-heating system[J]. Energy, 2014, 64: 375-388.

[2] JING Z X, JIANG X S, WU Q H, et al. Modelling and optimal operation of a small-scale integrated energy based district heating and cooling system[J]. Energy, 2014, 73: 399-415.

[3] 雷金勇,谢俊,甘德强.分布式发电供能系统能量优化及节能减排效益分析[J].电力系统自动化,2009,33(23):29-36.

LEI Jinyong, XIE Jun, GAN Deqiang. Optimization of distributed energy system and benefit analysis of energy saving and emission reduction[J]. Automation of Electric Power Systems, 2009, 33(23): 29-36.

[4] 王雁凌,李蓓,崔航.天然气分布式能源站综合价值分析[J].电力系统自动化,2016,40(1):136-142.DOI:10.7500/AEPS20150521003.

WANG Yanling, LI Bei, CUI Hang. Comprehensive value analysis for gas distributed energy station[J]. Automation of Electric Power Systems, 2016, 40(1): 136-142. DOI: 10.7500/AEPS20150521003.

[5] 贾宏杰,王丹,徐宪东,等.区域综合能源系统若干问题研究[J].电力系统自动化,2015,39(7):198-207.DOI:10.7500/AEPS20141009011.

JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of Electric Power Systems, 2015, 39(7): 198-207. DOI: 10.7500/AEPS20141009011.

[6] 顾伟,陆帅,王珺,等.多区域综合能源系统热网建模及系统运行优化[J].中国电机工程学报,2017,37(5):1305-1316.

GU Wei, LU Shuai, WANG Jun, et al. Modeling of the heating network for multi-district integrated energy system and its operation optimization[J]. Proceedings of the CSEE, 2017, 37(5): 1305-1316.

[7] 马腾飞,吴俊勇,郝亮亮.含冷热电三联供的微能源网能量流计算及综合仿真[J].电力系统自动化,2016,40(23):22-27.DOI:10.7500/AEPS20160426005.

MA Tengfei, WU Junyong, HAO Liangliang. Energy flow calculation and integrated simulation of micro-energy grid with combined cooling, heating and power[J]. Automation of Electric Power Systems, 2016, 40(23): 22-27. DOI: 10.7500/AEPS20160426005.

[8] 李正茂,张峰,梁军,等.含电热联合系统的微电网运行优化[J].中国电机工程学报,2015,35(14):3569-3576.

LI Zhengmao, ZHANG Feng, LIANG Jun, et al. Optimization on microgrid with combined heat and power system[J]. Proceedings of the CSEE, 2015, 35(14): 3569-3576.

[9] 王成山,洪博文,郭力,等.冷热电联供微网优化调度通用建模方法[J].中国电机工程学报,2013,33(31):26-33.

WANG Chengshan, HONG Bowen, GUO Li, et al. A general modeling method for optimal dispatch of combined cooling, heating and power microgrid[J]. Proceedings of the CSEE, 2013, 33(31): 26-33.

[10] 董朝阳,赵俊华,文福拴,等.从智能电网到能源互联网:基本概念与研究框架[J].电力系统自动化,2014,38(15):1-11.DOI:10.7500/AEPS20140613007.

DONG Zhaoyang, ZHAO Junhua, WEN Fushuan, et al. From smart grid to Energy Internet: basic concept and research framework[J]. Automation of Electric Power Systems, 2014, 38(15): 1-11. DOI: 10.7500/AEPS20140613007.

[11] 孙宏斌,郭庆来,潘昭光.能源互联网:理念、架构与前沿展望[J].电力系统自动化,2015,39(19):1-8.DOI:10.7500/AEPS20150701007.

SUN Hongbin, GUO Qinglai, PAN Zhaoguang. Energy Internet: concept, architecture and frontier outlook[J]. Automation of Electric Power Systems, 2015, 39(19): 1-8. DOI: 10.7500/AEPS20150701007.

[12] SHEIKHI A, RAYATI M, BAHRAMI S, et al. Integrated demand side management game in smart energy hubs[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 675-683.

[13] SHEIKHI A, BAHRAMI S, RANJBAR A M. An autonomous demand response program for electricity and natural gas networks in smart energy hubs[J]. Energy, 2015, 89: 490-499.

[14] SHEIKHI A, RAYATI M, BAHRAMI S, et al. A cloud computing framework on demand side management game in smart energy hubs[J]. International Journal of Electrical Power & Energy Systems, 2015, 64: 1007-1016.

[15] BAHRAMI S, SHEIKHI A. From demand response in smart grid toward integrated demand response in smart energy hub[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 650-658.

[16] ALBADI M H, EL-SAADANY E F. A summary of demand response in electricity markets[J]. Electric Power Systems Research, 2008, 78(11): 1989-1996.

[17] PALENSKY P, DIETRICH D. Demand side management: demand response, intelligent energy systems, and smart loads[J]. IEEE Transactions on Industrial Informatics, 2011, 7(3): 381-388.

[18] STACKELBERG V H. Marketform und gleichgewicht[M]. London: Oxford University Press, 1934.

[19] MAHARJAN S, ZHU Q, ZHANG Y, et al. Dependable demand response management in the smart grid: a Stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 120-132.

[20] MAHARJAN S, ZHU Q, ZHANG Y, et al. Demand response management in the smart grid in a large population regime[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 189-199.

[21] LEE J, GUO J, CHOI J K, et al. Distributed energy trading in microgrids: a game-theoretic model and its equilibrium analysis[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3524-3533.

[22] ASIMAKOPOULOU G E, DIMEAS A L, HATZIARGYRIOU N D. Leader-follower strategies for energy management of multi-microgrids[J]. IEEE Transactions on Smart Grid, 2013, 4(4): 1909-1916.

[23] TAN Z, ZHANG H, SHI Q, et al. Multi-objective operation optimization and evaluation of large-scale NG distributed energy system driven by gas-steam combined cycle in China[J]. Energy and Buildings, 2014, 76: 572-587.

[24] JU L, TAN Z, LI H, et al. Multi-objective operation optimization and evaluation model for CCHP and renewable energy based hybrid energy system driven by distributed energy resources in China[J]. Energy, 2016, 111: 322-340.

[25] WU Z L, DING J Y, WU Q H, et al. Two-phase mixed integer programming for non-convex economic dispatch problem with spinning reserve constraints[J]. Electric Power Systems Research, 2016, 140: 653-662.

[26] WEI F, JING Z X, WU P Z, et al. A Stackelberg game approach for multiple energies trading in integrated energy systems[J]. Applied Energy, 2017, 200: 315-329.

[27] NASH J F. Equilibrium points inn-person games[J]. Proceedings of the National Academy of Sciences of the United States of America, 1950, 36(1): 48-49.

[28] NASH J. Non-cooperative games[J]. Annals of mathematics, 1951, 54(2): 286-295.

[29] TOPKIS D M. Supermodularity and complementarity[M]. New Jersey, USA: Princeton University Press, 2011.

[30] VIVES X. Nash equilibrium with strategic complementarities[J]. Journal of Mathematical Economics, 1990, 19(3): 305-321.

[31] MILGROM P, SHANNON C. Monotone comparative statics[J]. Econometrica, 1994, 62(1): 157-180.

[32] TOPKIS D M. Comparative statics of the firm[J]. Journal of Economic Theory, 1995, 67(2): 370-401.

[33] MÜLLER A, SCARSINI M. Some remarks on the supermodular order[J]. Journal of Multivariate Analysis, 2000, 73(1): 107-119.

[34] BAHARLOUEI Z, HASHEMI M. Efficiency-fairness trade-off in privacy-preserving autonomous demand side management[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 799-808.