计及回水管网热损失的电热联合系统潮流模型及算法

刘述欣, 戴 赛, 胡林献, 丁 强, 王其祥

(1. 哈尔滨工业大学电气工程及自动化学院, 黑龙江省哈尔滨市 150001; 2. 国网烟台供电公司, 山东省烟台市 264000; 3. 中国电力科学研究院有限公司, 北京市 100089)

0 引言

随着风电装机容量的不断增长,弃风问题也越来越严重[1]。由于热网负荷与风电场出力的变化趋势大致呈同向特性,而热网负荷、风电场出力与电网负荷的变化趋势大致呈反向特性[2],各种解耦热电机组热电耦合,通过电力系统与热力系统协调优化运行来提高电力系统调峰能力及风电消纳率的方案被不断提出[3]。

电热联合系统是典型的多能量流网络系统,其潮流计算是其他各种分析计算的基础。但有别于成熟的电力系统潮流计算,目前国内外涉及电热联合系统潮流计算的研究不多。文献[4-5]提出了几种热网建模方法,但模型简单、模拟程度不高。文献[6]建立了一种较为完备的热网模型,但不能快速、简洁地求解模型。文献[7]针对多热源环状热网水力工况分析所涉及的非平面网及故障工况供回水管网不对称的问题,基于图论提出了一种建立空间热网拓扑结构的方法。

现有方法的一大特点是热力系统模型完全参照电力系统构建,如参照基尔霍夫电流方程及欧姆定律方程分别建立了流量连续方程、压强损失方程和热网热力模型。但输电网与热网有很大差别,如高压输电网是环网而热网是辐射状;输电网三相对称不需要考虑回线损耗,而热网的供水、回水管网上都有热损失。为了统一电网和热网模型,传统热力系统模型不得不假设了一个回水混合温度,并将整个回水管网温度固定在这个温度。传统热网模型不仅与实际热力系统不符,而且会造成较大的计算误差。文献[8]建立了含热网约束的电热能源集成系统运行优化模型,虽然考虑了回水节点的温度差异,但其计算模型需建立复杂的关联求解矩阵,计算速度慢且计算量大。

本文首先研究热网的水力、热力模型,分析实际供热网络的辐射状结构特点及其运行方式,提出了计及回水管网热损失的热力系统潮流计算递推模型及其快速算法;然后研究了热力系统、电力系统耦合模型,热电机组发电功率和电锅炉消耗电功率的计算方法,以及电热联合系统潮流计算过程;最后通过算例及其与传统模型的对比分析,验证了本文算法的正确性与有效性。

1 热力系统传统模型

1.1 热力系统结构

热力系统由热源、热网和热负荷组成,其中热网又由拓扑结构完全相同的供水网络和回水网络组成[4-5],其结构如附录A图A1所示。

热网络变量包括各节点压强hi、各负荷需水量Li、节点i和j之间的管道水流量mij。热量传输过程中,由于管道粗糙,管道中的热水需克服管壁做功,加上管道向外散热,因此从热源节点到热负荷节点会有热损耗。在热负荷i处,热水通过热交换器为用户提供热量,继而将冷却的水通过回水网络返回产热源,进行下一次加热。供、回水网络中各管道流量近似一致,但由于2个网络中水温不同,会影响水的密度、黏度、雷诺数等[6-8],造成2个网络中水流量略有不同。为简化计算,一般对此忽略不计[9]。

1.2 热网水力模型

热网水力模型用于确定各管道水流量及各节点的注入水流量。供水网络与回水网络拓扑相同,所以只针对供水网络进行分析。水力模型中存在水流量连续方程及压强损失方程,分别对应于电力系统的基尔霍夫电流方程及欧姆定律方程[6,10-11]。

1)流量连续方程。流量连续方程是指水流进入节点的水流量等于流出节点的水流量加上节点消耗的水流量,其具体公式为:

Am=mq

(1)

式中:A为管道支路相对于节点的关联矩阵;m为供水管道水流量;mq为节点注入水流量。

2)压强损失方程。压强损失方程表征管道内压强损失与水流量的关系[6],其具体方程为:

hf=Km|m|

(2)

式中:K为各个供水管道的阻抗系数,K值主要取决于管道直径、液体物理性质[11],具体求解公式如式(3)所示。

(3)

式中：ε为管道的绝对粗糙度值;D为管道的直径。

水力模型可视作一个普通的水管道网络,水管道网络求解有2种基本方法,即压强法[4,7,10]和环流法[10,12],分别对应电路中的节点电压法和节点电流法。

1.3 热网热力模型

热力模型确定热网节点温度。热网节点包含2个温度信息(见附录A图A2):各节点供给(负荷输入)温度Tsi、各节点返回(负荷输出)温度Tri。影响节点返回温度Tri的主要因素为:节点供给温度Tsi、外界自然温度,以及热负荷的大小。

供水管网各节点温度为:

(4)

式中:Ten为外界自然温度;λ为管道每米传输阻抗;dij为管道传输距离;Cp为水的比热容。

传统模型忽略回水管网热损失,将各节点回水温度统一至回水混合温度:

(5)

式中:n为节点数。

利用水力模型求得各供水管道的水流量数据,在热力模型中考虑热网热量关系、热传递、热损等条件后确定热网节点的两个温度信息。对于热力系统潮流计算,热力模型与水力模型缺一不可,热力模型决定各节点的温度数据,水力模型决定各管道水流量,二者输出数据互为输入。

2 热力系统递推模型

2.1 实际热网结构与运行特点

实际生产中,每个热源(如热电厂)固定供给特定地区热负荷,各热源之间或者不相连,或者有管道相连但管道通常处于关闭状态,这使得热网结构不同于输电网的环网结构,而是类似于电力系统中的配电网,为辐射状结构(见附录A图A3),且热功率也是单方向流动,因此应参照配电网建模。

实际热网运行方式分为质调节和量调节两种:质调节是保持热源节点出口流量不变,通过调节热源出口温度来适应热负荷变化;量调节则是保持热源出口温度不变,通过调节热源节点出口流量来适应热负荷变化。由于量调节时阀门动作频繁,对阀门损耗较大,故一般采取质调节方式。

2.2 热力系统潮流递推模型

综合考虑热网模型与实际热网结构特点,可得如下热力系统潮流递推模型。

管道水流量计算模型为:

(6)

式中:φi为节点i的热负荷;φEBi为节点i电锅炉发出的热功率;H为热网节点集合。

供水网络节点温度之间的关系如式(4)所示。区别于传统模型,本文模型计及回水管网热损失后,回水网络节点温度之间的关系为:

(7)

热源供热功率Ds与供回水温度、流量的关系为:

Ds=Cpmha(Tsha-Trha)

(8)

式中:Tsha,Trha,mha分别为热源节点a的出口水温、回水温度和出口流量。

上述热网模型及运行方式与配电网潮流计算模型及运行方式类似,因此也可采用前推回代法计算。

前推:利用各负荷节点信息,从末节点出发,逆着热功率传递方向,利用式(6)前推确定各管道及节点的注入水流量。

回代:利用前推过程求出的水流量信息,从热源节点出发,顺着热功率传递方向,利用式(4)、式(7)确定各热负荷节点的供给温度、返回温度等信息。

3 电热联合系统潮流计算

3.1 热力系统潮流计算流程

步骤1:初始化所有节点供给温度及出口流量。

步骤2:前推运算。计算各热负荷节点注入水流量、各管道水流量。

步骤3:回代运算。计算各热负荷节点供给温度、返回温度及节点压强。

步骤4:计算热源节点返回温度。

步骤5:迭代收敛判断,若前后两次误差在允许范围内则输出结果,否则返回步骤2。

步骤6:计算各热源的供热功率。

3.2 电热耦合计算模型

采用抽凝热电机组、电锅炉等能量转换设备后,电网、热网紧密耦合。

1)背压机组(抽凝机组可等值成纯凝机组与背压机组)产生电能和热能[5]满足如下关系:

(9)

式中:φB为背压机组发出的热功率;PB为背压机组发出的电功率;Cm为产热产电比,为一常数。

2)电锅炉等能量转换设备有:

(10)

式中:PEB为电锅炉消耗的电功率;φEB为电锅炉发出的热功率;Z为电锅炉的电热比,为一常数。

3.3 电力系统潮流计算

热力系统潮流计算结束后,根据(9)、式(10)即可计算等值背压机组发出的电功率和电锅炉消耗的电功率。然后采用牛顿—拉夫逊法计算电网潮流,牛顿—拉夫逊法已非常成熟[13-15],本文不做赘述。

4 算例分析

4.1 算例系统

算例系统的热网部分由两个独立的供热网络组成,如图1所示。电网部分则采用IEEE 5机14节点系统[16]。热网部分的热源节点S1和S2分别对应电网中的节点10和11,为背压机组。调峰电锅炉分别装设在热网节点5和15,调峰比(即电锅炉的供热功率占总热负荷的百分比)k取0.4。节点14为风电场,且选为平衡节点,以方便分析电热联合系统的风电消纳情况,剩下的节点12和13为火电机组。

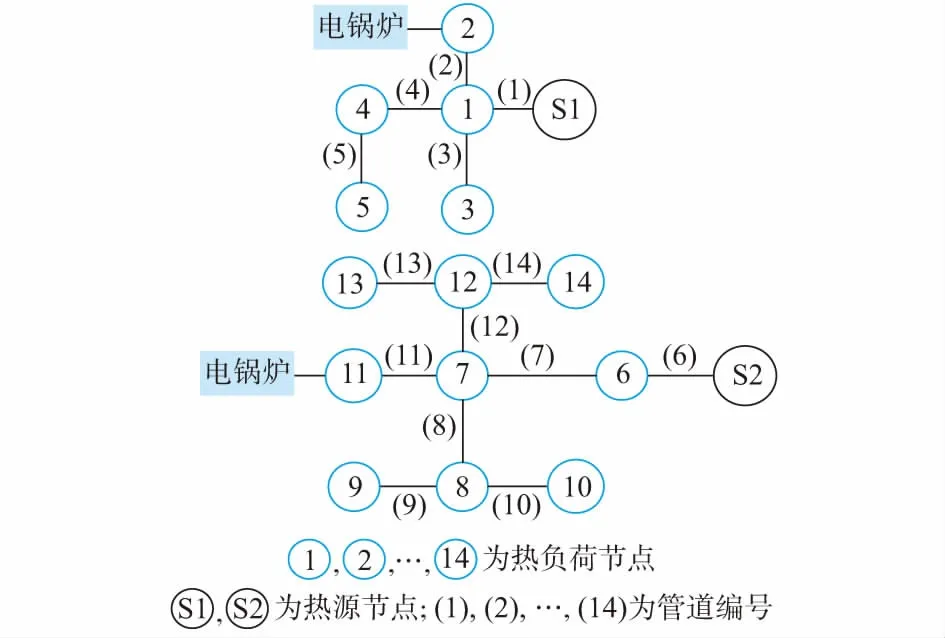
图1 供热网络结构Fig.1 Topology of thermal grid

4.2 潮流计算结果

热源节点S1和S2的出口温度设为95 ℃,1号、6号管道出口流量分别设为0.4 kg/s和0.6 kg/s。热电机组产热产电比Cm取0.76,电锅炉的电热比取1.3[11]。本文相较于其他研究热力系统文献的一个突出特点是在建模过程中计及了热网回水管网热损失,而传统模型将此要素忽略,将所有返回温度均设为定值。本节将传统模型与本文模型进行对比,潮流计算结果对比如附录A图A4、图A5所示。

回水管网热损失对热力系统潮流的影响较大,管道水流量最大偏差率为6.6%(4号管道),节点返回温度的最大偏差率为18.5%(节点7)。如此大的偏差会严重影响潮流模型的仿真效果,以至于热网数据代入电力系统潮流计算中时,由于误差累计的原因,会使得最终联合系统潮流结果严重失真。两种模型在热源节点处的计算结果对比如表1所示。

表1 两种模型下的热源节点计算结果对比Table 1 Computation result comparison of heat source nodes in two models

从表1中可见,在相同的出口水温及出口流量条件下,本文提出的计及回水管网热损失的新型算法的热源供热功率要比传统算法多出4.1%。面对如此大的误差,可以证明回水管网热损失会严重影响传统算法计算发电机抽汽量等数据,很难为实际生产提供数据参考,因此不可忽略。

4.3 电锅炉位置对热力系统潮流及风电消纳率的影响

将电锅炉依次安装在热网首端(节点1和6)、中段(节点4和12)及末端(节点5和14)上,且电负荷分别由电网中节点10和11承担。调峰比、热源出口温度保持不变时,潮流计算结果如附录A图A6及表2所示。

表2 不同电锅炉位置下的热源节点计算结果对比Table 2 Computation result comparison of heat source nodes with different location of electric boiler

在附录A图A6中,安装调峰电锅炉会影响热力系统的潮流分布,且靠近电锅炉的位置所受影响较大,从安装位置处到热源节点的传输路径上的管道都有所影响。这是由于电锅炉作为补充热源承担了一部分热网热负荷,热负荷节点对从热源注入的水流量依赖性降低,管道水流量减少。例如:电锅炉安装在节点5和14处时,其管道流量明显低于未安装电锅炉的情况,且作为节点5和14供水网络中的中间管道,节点4和12的管道流量也明显降低。

由表2可见:电锅炉安装位置距离热源越远,热源供热功率越少,联合系统消纳风电能力越强。这是因为安装位置影响系统主干管道水流量,进而影响管道传输损耗,达到影响供热功率的效果。风电上网功率变化较小的原因是电锅炉设定容量数量级为风电机组基准值的1%,故其波动仅为0.06%。

4.4 热源出口水温对热力系统潮流及风电消纳率的影响

热网采用质调节,在保证热源节点出口流量不变的情况下,通过调节出口水温来实现热网热量平衡。假设出口水温分别为95,85,75 ℃,其他条件不变时,引起管道流量偏差结果如附录A图A7所示。

从附录A图A7易见,改变热源出口温度时,管道水流量的波动量很小,这是因为热网采用质调节,热源出口水流量被限制为一定值,为满足热网热功率平衡,只能通过改变热源返回温度来实现,如表3所示。

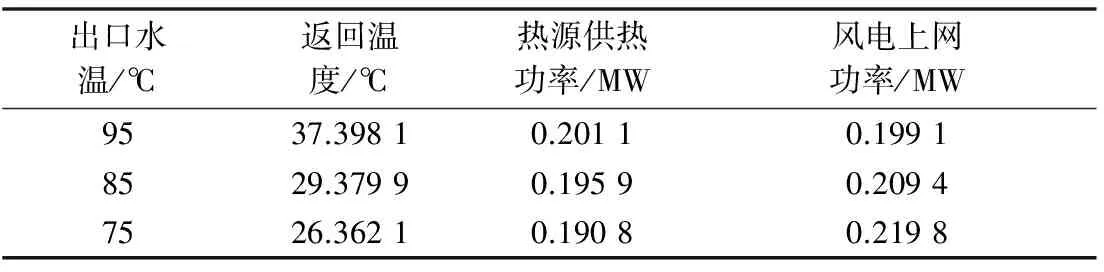
表3 不同热源出口温度下的热源节点计算结果对比Table 3 Computation result comparison of heat source nodes with different heat source export temperatures

随热源出口水温的下降,热源返回温度也随之下降,符合实际,且热源出口水温越高,管网热损耗越大对应所需的供热功率越大,根据“以热定电”的约束可知,对应背压热电机组的必发电功率必然增加,由于电网部分电负荷不变,此消彼长,风电上网功率(用平衡节点功率表征)必然受到压缩。

4.5 热源出口流量对热力系统潮流及风电消纳率的影响

将1/6号管道出口流量依次设为0.3/0.5,0.4/0.6,0.5/0.7 kg/s,保持其他条件不变,引起管道水流量变化结果如附录A图A8所示。

附录A图A8中,改变热源出口流量会显著影响管道水流量。改变热源出口水流量后,要维持热网热功率平衡,必须通过改变返回温度实现,如表4所示。热源出口流量越高,根据式(5)可知供给温度与返回温度之差必然降低,与实际相符,且出口流量越大,管网损耗越大对应热源供热功率越大,同理于改变热源出口水温的情况,风电上网机会减少,风电消纳率降低。

表4 不同热源出口流量下的热源节点计算结果对比Table 4 Computation result comparison of heat source nodes with different heat source export flows

5 结论

1)热力系统结构、运行方式与配电网类似,因此应参照配电网建模。

2)回水管网热损失较大,会严重影响热力系统潮流计算结果,不可忽略。

3)本文建立的热力系统递推模型不仅计及了回水管网热损失,而且可方便处理多分支辐射热网及其电锅炉等能量转换装置。

4)本文模型无需解算热网水力模型,无需复杂的网络编号,也不用形成导纳矩阵,编程简单、计算速度快。

5)提高热源出口水温及增加出口流量会增加热源供热功率,对应热电机组必发功率增加,电网出现供大于求的情况,为了保证功率平衡,风电机组(算例中的平衡节点)上网机会被压缩,风电消纳率降低。

未来本课题可以着重研究一个相对较长的调度周期内,考虑热电运行模式对风电消纳的影响。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 张冲,胡林献,胡佳.热电机组比重及热负荷对风电消纳率影响的研究[J].电力系统保护与控制,2013,41(23):120-125.

ZHANG Chong, HU Linxian, HU Jia. Research on the impact of the proportion of thermal power generating units and heat load on the wind power accommodation rate[J]. Power System Protection and Control, 2013, 41(23): 120-125.

[2] 邓佳乐,胡林献,李佳佳.采用二级热网电锅炉调峰的消纳弃风机理及经济性分析[J].电力系统自动化,2016,40(18):41-47.DOI:10.7500/AEPS20151001001.

DENG Jiale, HU Linxian, LI Jiajia. Analysis on mechanism of curtailed wind power accommodation and its economic operation based on electric boiler for peak-load regulation at secondary heat supply network[J]. Automation of Electric Power Systems, 2016, 40(18): 41-47. DOI: 10.7500/AEPS20151001001.

[3] 吕泉,姜浩,陈天佑,等.基于电锅炉的热电厂消纳风电方案及其国民经济评价[J].电力系统自动化,2014,38(1):6-12.DOI:10.7500/AEPS201206124.

LYU Quan, JIANG Hao, CHEN Tianyou, et al. Wind power accommodation by combined heat and power plant with electric boiler and its national economic evaluation[J]. Automation of Electric Power Systems, 2014, 38(1): 6-12. DOI: 10.7500/AEPS201206124.

[4] BOHM B, HA S, KIM W, et al. Simple models for operational optimization[R]. Kongens Lyngby, Denmark: Technical University of Denmark (DTU), 2002.

[5] STEER K C B, WIRTH A, HALGAMUGE S K. Control period selection for improved operating performance in district heating networks[J]. Energy and Buildings, 2011, 43(2/3): 605-613.

[6] LIU X, JENKINS N, WU J, et al. Combined analysis of electricity and heat networks[D]. Cardiff, UK: Cardiff University, 2014.

[7] 王晓霞,赵立华,邹平华,等.基于图论的空间热网拓扑结构[J].计算物理,2014,31(2):207-215.

WANG Xiaoxia, ZHAO Lihua, ZOU Pinghua, et al. Topology structure of spatial heat-supply network based on graph theory[J]. Chinese Journal of Computational Physics, 2014, 31(2): 207-215.

[8] 顾泽鹏,康重庆,陈新宇,等.考虑热网约束的电热能源集成系统运行优化及其风电消纳效益分析[J].中国电机工程学报,2015,35(14):3596-3604.

GU Zepeng, KANG Chongqing, CHEN Xinyu, et al. Operation optimization of integrated power and heat energy systems and the benefit on wind power accommodation considering heating network constraints[J]. Proceedings of the CSEE, 2015, 35(14): 3596-3604.

[9] 董今妮,孙宏斌,郭庆来,等.热电联合网络状态估计[J].电网技术,2016,40(6):1635-1641.

DONG Jinni, SUN Hongbin, GUO Qinglai, et al. State estimation for combined electricity and heat networks[J]. Power System Technology, 2016, 40(6): 1635-1641.

[10] BARGIELA A. On-line monitoring of water distribution networks[D]. Durham, UK: Durham University, 1984.

[11] LIU X. Combined analysis of electricity and heat networks[D]. Cardiff, UK: Cardiff University, 2013.

[12] ARSENE C T C, GABRYS B. Mixed simulation-state estimation of water distribution systems based on a least squares loop flows state estimator[J]. Applied Mathematical Modelling, 2014, 38(2): 599-619.

[13] 陈海焱,陈金富,段献忠.含分布式电源的配电网潮流计算[J].电力系统自动化,2006,30(1):35-40.

CHEN Haiyan, CHEN Jinfu, DUAN Xianzhong. Study on power flow calculation of distribution system with DGs[J]. Automation of Electric Power Systems, 2006, 30(1): 35-40.

[14] 滕予非,宁联辉,李甘,等.含分频风电的电力系统潮流计算方法以及稳态特性分析[J].电力系统自动化,2014,38(22):56-62.DOI:10.7500/AEPS20131224009.

TENG Yufei, NING Lianhui, LI Gan, et al. A power flow calculation method and steady state characteristics of power system with fractional frequency wind power system[J]. Automation of Electric Power Systems, 2014, 38(22): 56-62. DOI: 10.7500/AEPS20131224009.

[15] 王云鹏,韩学山,孙东磊,等.基于交直流关联最小雅可比矩阵结构的潮流算法[J].电力系统自动化,2015,39(7):1-6.DOI:10.7500/AEPS20140514001.

WANG Yunpeng, HAN Xueshan, SUN Donglei, et al. A power flow algorithm based on minimum Jacobian matrix for AC/DC hybrid systems[J]. Automation of Electric Power Systems, 2015, 39(7): 1-6. DOI: 10.7500/AEPS20140514001.

[16] 卢志刚,张静,程慧琳,等.基于分解协调及外网浓缩等值的多代理状态估计[J].电力系统自动化,2012,36(14):23-29.

LU Zhigang, ZHANG Jing, CHENG Huilin, et al. Multi-agent state estimation based on decomposition and coordination and external network concentration equivalence[J]. Automation of Electric Power Systems, 2012, 36(14): 23-29.