改进小波包阈值算法在振动信号去噪中的应用

吕楠楠，苏淑靖，翟成瑞

(中北大学电子测试技术重点实验室，山西 太原 030051)

0 引言

火箭发射过程中，对已获取的发射塔架振动信号的降噪处理是十分重要的。火箭发射过程中发射塔架会受到不同程度的激震，使其受到一定损坏；随着时间积累，发射塔架的状态会随着火箭发射次数的增加而越来越不稳定。因此，在火箭发射任务结束后，必须对发射塔架的健康状况进行评估，并进行相应的维护才能为下次发射任务的顺利完成提供保障[1]。在实际中，火箭发动机喷射出高速的燃气射流温度高达3 000 ℃，形成的压力冲击以气浪形式作用于发射塔架，从而产生载荷同时引起塔架激励，其间产生的冲击波传播速度较快且迅速衰减，紧随冲击波段之后是杂乱无章的压力脉动阶段。同时超音速紊流产生的噪声引起塔架上设备的激振[2]。此时，由于瞬时性，信号的衰耗随时间的变化不能忽略，需考虑信道中存在的畸变、衰减等复杂关系。所以在火箭发射塔架层2的振动信号中，需同时考虑加性噪声和乘性噪声。

在降噪过程中，文献[3]中通过设计基于小波变换的滤波器来对信号消噪，但对高频部分仍无法频率细分。相比之下，小波包去噪能够根据被分析处理信号的特征，自适应的选取与信号对应的频带，从而能够与被分析处理信号的频谱相匹配。文献[4]提出的改进小波包阈值算法中通过确定不同的阈值参数进而确定相应的阈值，该方法与大多传统小波包去噪法相似，去噪过程仅仅针对加性噪声，不能有效去除乘性噪声。本文针对上述问题，提出了一种基于小波包系数阈值降噪的改进算法。

1 小波包阈值去噪原理

对于给定正交尺度函数及其所对应的小波函数，存在双尺度方程：

(1)

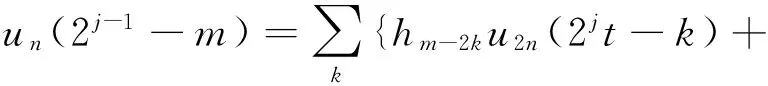
(2)

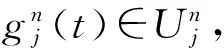
(3)

(4)

图1是小波包变换对信号进行三层分解的结构图。小波包变换在对信号进行降噪时，会分解其所有的低频子带和高频子带，相较于小波包变换，小波包变换的局部分析能力更加精确。

传统的小波包阈值去噪的方法理论是：首先选择一个正交小波基，对被处理信号f(t)进行N层小波包分解；然后通过计算得出最优小波树，针对每个分解后的小波包系数，都选取一个合适的阈值进行阈值量化；最后通过小波包重构得到原始信号估计值。

2 改进的小波包阈值去噪算法

常见的小波包去噪都是针对加性噪声的[7]，本文通过对小波包去噪算法的改进，在去除加性噪声的基础上可去除乘性噪声。

首先，进行第一次分解重构。对被处理信号f(t)进行N层小波包分解(本文选用db5小波基函数)，对1～N层小波系数进行阈值滤波，去除加性噪声n(t)，得到n1(t)g(t)。表示为如式(5)：

(5)

对经过阈值滤波的小波包系数进行重构，得到信号f1(t)。因为信号f1(t)与乘性噪声在统计上是相互独立的，对f1(t)进行对数运算后，将乘性噪声转换为加性噪声。表达式如下：

lb(n1(t)g(t))=lb(n1(t))+lb(g(t))

(6)

然后，进行第二次分解和重构。对lb(n1(t)g(t))进行N层小波包分解(本文选用db7小波基函数)，对1～N层小波包系数进行阈值处理，去除掉噪声lb(n1(t))对应的小波包系数，得到lb(g(t))对应的小波包系数。最后对第二次去噪后的小波包系数进行重构，得到lb(g(t))。表达式如下：

(7)

最后，对lb(g(t))进行指数运算，得到复原后信号g(t)。运算方法如下：

(8)

在上述步骤中阈值函数的选取较为关键，常用的阈值函数有硬阈值函数和软阈值函数[8]。硬阈值函数定义为：

(9)

软阈值函数定义为：

(10)

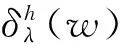
(11)

当a为0时，上式变为硬阈值函数；a为1时上式等效于软阈值函数；a取0与1之间的数，w→±时，则有|δλ(w)-w|→aλ，也就是说随着|w|的增大，δλ(w)和w的偏差的绝对值逐渐减小为aλ，所以大大减小了软阈值方法中出现的恒定偏差，重构精度明显提高，增强了去噪效果[12]。所以我们只需在0和1之间适当选择a值，就会得到更好的去噪效果。

3 测试原理及测试数据分析

在对振动参数进行测试时，大量的噪声成分包含在了振动参数中，因此寻求高精度与高区分度的发射环境下发射塔架振动参数降噪处理和特征分析方法，对发射塔架在发射过程中由于振动造成对健康状况的影响评估提供依据有重要意义。

3.1 测试过程及测试数据

振动信号测试方案框图如图2所示，测量系统由振动加速度传感器、变送器、采编存储器、测控计算机及电缆组成。传感器布设于发射塔架层2，通过不燃电缆与变送器连接。变送器布置与隔离带后，将传感器输出的电压信号转变成抗干扰性强的电流信号，变送器与采编存储器通过抗干扰电缆连接。采编存储器布置于发射场的设备间，通过USB电缆与测控计算机通信。

图2测试方案中，ADC的分辨率为16位，以5 KHz进行采样；通过FPGA读取ADC采集的数据并进行编帧(每1 ms采集的数据编为一帧)，然后将测试数据存储到Flash中；采编存储器通过USB数据线将数据读入到测控计算机。在火箭点火后进入点火延迟阶段，接着，从起飞到离开塔架在瞬间完成，实测振动波形如图3(a)所示。本文截取其中能量集中部分进行分析，对采样点个数重排后如图3(b)所示。

3.2 测试数据去噪处理与分析

在选取处理发射塔架振动参数的小波基时，应该考虑其在一定区间的紧支性、近似的对称性及足够的消失矩，Daubechies小波系、Symlets小波系和Coiflets小波系均满足上述要求，由于小波基的选取

对本文改进算法的研究没有实质性影响，本文从其中选取Daubechies小波系。

在本文改进算法中，对所测得的振动参数，首先选用db5小波基进行3层分解，去除加性噪声；然后选用db7小波基进行3层分解，去除乘性噪声。统一采用Rigrsure阈值。

在计算信噪比与均方根误差过程中，振动参数的信噪比(SNR)为：

(12)

振动参数的均方根误差(RMSE)为：

(13)

其中，未经降噪的振动信号为x(i)，经过降噪后的振动信号为x＾(i)。

3.2.1三种阈值函数降噪效果比较

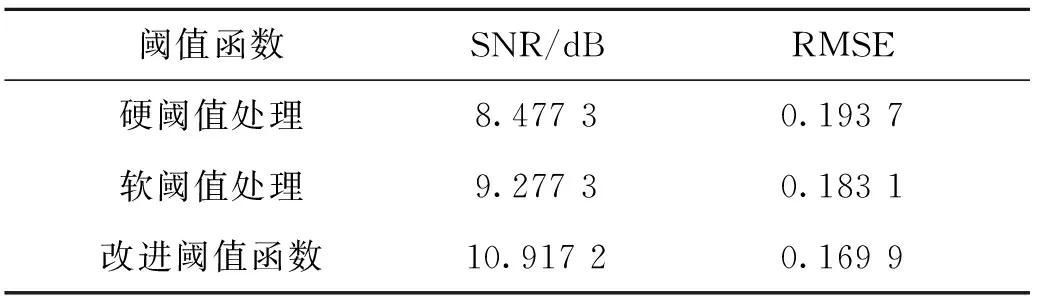
图4、图5、图6是分别选取硬阈值函数、软阈值函数、改进阈值函数三种不同阈值函数降噪的结果，表1是使用Matlab计算得到三种不同阈值函数去噪后的信噪比与均方根误差值。

阈值函数SNR/dBRMSE硬阈值处理8.47730.1937软阈值处理9.27730.1831改进阈值函数10.91720.1699

从图4看出，虽然硬阈值函数去除了信号中的部分噪声，但由于其去噪过程中将小于阈值的点均处理为0，大于或等于阈值的点保持不变；并且处理得到的小波包系数值在阈值处是不连续的，所以从图中可看出重构所得的信号出现振荡；噪声信号没有被很好的滤除掉。从图5看出软阈值函数消除了在阈值处的不连续，去噪信号平滑，没有产生附加振荡，但该方法的去噪效果较依赖信噪比的大小，对于高信噪比信号适合该方法，而本文采集的振动信号由于环境恶劣，去噪效果不理想，在滤除噪声成分的过程中，信号的有用信息特征同时被滤掉。图6改进阈值函数去噪通过减小软阈值方法中出现的恒定差使重构精度提高；在去除了高、低频的噪声信号的基础上，也保留了原始信号的细节特征。从表1可直观地看出改进阈值函数降噪后信噪比高于硬阈值函数和软阈值函数，并且均方根误差最小。所以本文对振动信号的降噪采用改进阈值函数。

3.2.2改进小波包去噪与经典小波包去噪比较

对振动信号降噪采用改进阈值函数，图7是经典小波包降噪效果图，图9是改进小波包阈值降噪(改进小波包二次去噪)效果图，图8是改进小波包去噪过程中第一次降噪效果图。在图7与图9两种不同去噪算法下，利用MATLAB计算出信号降噪后信噪比与均方根误差值如表2所示。

阈值函数SNR/dBRMSE经典小波包阈值处理12.48900.1437改进小波包阈值处理14.67320.1210

图7传统小波包采用sym5小波基去噪效果图，图8是选用db5小波基一次去噪效果图，二者均是仅仅去掉信号中加性噪声的效果图，且其去噪后信号较尖锐，毛刺较多，平滑性较差。与图7和图8相比，图9是将一次去噪信号重构和对数运算后，选用db7小波基进行二次去噪后的效果图，与图7和图8比较可看出，不仅去除了加性噪声，也同时去除掉乘性噪声，且信号平滑性较好。由表2可直观看出，与传统小波包算法相比，改进小波包算法降噪后信号的信噪比提高了2.2 dB，均方根误差降低。

如图10和图11所示，横轴为频率，纵轴为为功率谱。主振频率即为最大振幅所对应的频率，从图10中可知振动参数的主振频率为310 Hz，能量主要集中在0～600 Hz。图11与图10对比分析，改进小波包降噪后能量特征和细节特征保留较好。

通过上述实验分析，针对某些噪声信号的分布特性，传统的小波包去噪处理存在局限性，而本文改进的算法在去除加性和乘性噪声的同时有效的保护各频段的有用信息，为小波和小波包阈值去噪准则提供了一种思路。

4 结论

本文提出了一种基于小波包系数阈值降噪的改进算法。该算法采用改进阈值函数，通过两次小波包分解和重构对信号降噪，第一次按照传统小波包去噪法去除加性噪声；第二次将分解后的小波包系数进行对数运算并采用阈值去噪法消除信号中乘性噪声。实验结果表明，改进算法相比于传统算法信噪比提高了2.2 dB，且均方根误差降低；结合傅里叶变换，改进算法较好的保留原始信号的能量特征及细节特征。不论是在主观上还是实际对比结果上，改进算法去噪效果明显高于传统算法。

[1]杨露,沈怀荣.空射火箭发射环境及测试方法分析[J].导弹与航天运载技术，2006,286(6):24-28.

[2]尹续峰,刘晓华.发射气流冲击对塔架结构受力影响的实测与分析[J].建筑结构，2007,37(4):42-44.

[3]彭志科,卢文秀,褚福磊.新的基于小波变换的振动信号消噪法[J].机械工程学报，2006,42(4):18-22.

[4]郑建国,石智,权豫西.非平稳信号的小波包阈值去噪方法[J].信息技术，2007,3(5):16-19.

[5]李红延,周云龙,田峰等.一种新的小波自适应阈值函数振动信号去噪算法[J].仪器仪表学报，2015,36(10):2200-2205.

[6]时合生,王启明.小波去噪仿真研究与实验[J].计算机与数学工程,2014,42(4):739-742.

[7]刘珍.基于振动信号的结构模态参数识别与损伤分析[D].西安：西安电子科技大学，2010.

[8]Ning J X,Wang J H,Gao W Z.A wavelet-based data compression technique for smart grid[J].IEEE Transactions on Smart Grid,2011,2(1):212-218.

[9]Riji R,Keerthi A S Pollao,Madhu S Nair, et al.Fuzzy based directional weighted median filter for impulse noise detection and reduction[J].Fuzzy Inf Eng, 2012,4:351-369.

[10]彭志科,卢文秀,褚福磊.新的基于小波变换的振动信号消噪方法[J].机械工程学报,2006,42(4):18-22.

[11]王宏强,尚春阳,高瑞鹏,等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击,2011,30(10):165-168.

[12]王彦青,魏连鑫.一种改进的小波阈值去噪算法[J].上海理工大学学报,2011,33(4):405-408.