基于动态RCS的机动目标探测概率计算方法
2018-03-12黄亚林张晨新张小宽孙铭才
黄亚林,张晨新,张小宽,孙铭才
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
随着科技的不断进步,现代战机集隐身性能、高灵敏度、高精确度以及实时态势感知于一身,可以在不同的战斗形势下迅速作出对应的复杂机动。尤其是以F-22,F-35为代表的第五代战机给世界各国的防空领域带来了巨大的挑战,如何提高防空雷达对先进战机的探测能力成了世界性的研究难题。
目前,目标探测概率计算所采用的RCS数据主要是依靠已有的RCS统计模型直接生成或直接将RCS视为定值[1-3]。对于运动目标而言,这两种做法都存在相应的局限性,不能客观反应目标RCS同飞行姿态变化之间的关系。在飞机实际飞行过程中,其飞行轨迹具有高度的任意性,随飞行员瞬时的操作意图而变化。同时,RCS又是姿态敏感函数,姿态角的微小变化都可能引起RCS的剧烈起伏[4-5]。因此,基于动态RCS数据的运动目标探测研究更加贴近实际,相关领域也取得了许多成果。陈世春等[6]从探测概率角度对飞机的隐身性能进行了分析,研究了4种典型隐身飞机RCS起伏数据与探测概率的关系。戴崇等[7]利用动态RCS数据分析了卡方分布在一定发现概率下自由度与信噪比的关系。晏青等[8]综合了动态RCS数据与雷达距离的探测概率模型,对无人机的航迹规划进行了研究。本文综合考虑影响隐身目标探测的主要方面,基于隐身目标的精确模型和目标航迹的精确建模提出了一种基于动态RCS数据的探测概率计算方法。
1 航迹建模及动态RCS电磁计算方法
1.1 飞行原理分析
用于航迹建模的目标模型通常分为3自由度和6自由度模型。其中3自由度模型将目标视为质点,只包含飞行的力方程和质心方程,能够较好地反映飞机的航迹特性。在侧重飞行航迹特性和飞行性能时可用作简化模型。6自由度模型将目标视为刚体,不仅涵盖了力方程和质心方程,还包含了力矩方程和姿态角方程,能够更加全面地反映飞机运动机理,更加贴近实际飞行效果。6自由度模型的动力学方程为[9-10]:

(1)
式中,m,G分别为飞机质量和飞机重量;Vx,Vy,Vz为速度矢量在各坐标轴上的投影;Fx,Fy,Fz为除重力以外其余力的合力在各坐标轴上的投影;wx,wy,wz为旋转角速度在各坐标轴上的投影;θ,γ分别为俯仰角和滚转角。
质心运动方程:
(2)
其中,
(3)
式中,θ,ψ,γ分别为飞机的俯仰角,偏航角和滚转角,统称欧拉角[11]。(x,y,z)为飞机在地面雷达坐标系下的直角坐标。
1.2 航迹建模
1.2.1平飞
平飞是一种最基本的飞行方式,速度恒定,无倾斜,航迹偏转角恒定,滚转角恒为0,升力等于重力,推力等于阻力。将速度取值400 m/s,航路捷径取为10 km,平飞航迹的三维显示如图1。
1.2.2俯冲
典型俯冲航迹可分为三段:进入俯冲段,俯冲段,退出俯冲段。目标俯冲时,随着高度逐渐下降,速度不断增大,到达某一高度时,迎面阻力等于推力与重力在速度方向的分量之和时,速度达到最大,该速度称为极限速度。俯冲段航迹与水平面的夹角λ称为俯冲角。λ的变化范围通常在20°~60°之间[12]。取俯冲角为45°,速度为400 m/s,合理设置进入俯冲段与俯冲段及俯冲段与退出俯冲段之间的衔接时间,使转换过程平滑,所得俯冲航迹的三维显示如图2。
1.2.3特定军事背景下的航迹建模
实际军事作战和训练中,飞机机动往往是几组简单的灵活组合,以达到某种军事目的。图3给出了一种战斗机执行完轰炸任务后迅速脱离险境的机动航迹,它是集俯冲、拐弯、平飞于一体的一种实用性战术机动动作。
1.3 动态RCS的电磁计算方法
动态RCS计算的前提是目标机动姿态变化的提取,目标在预定航迹中飞行时,由雷达方给出的RCS是随时间连续变化的,这是雷达视线在目标坐标系中随时间变化和目标自身姿态变化所致。因此,还需根据目标在雷达坐标系航迹和姿态变化,进行坐标变换,求出雷达视线在目标坐标系中随时间变化的方位角和俯仰角。
1.3.1目标坐标系定义及坐标转换
目标坐标系OXYZ如图4,坐标原点位于目标中心,X轴平行于机身轴线指向前方,Z轴位于目标对称平面内,垂直于X轴指向上方,Y轴垂直于目标对称平面,指向由右手法则确定[13]。
从雷达坐标系到目标坐标系的变换过程可由式(4)表示:
(4)
式中,(x(t),y(t),z(t))为雷达坐标系中任意一点坐标,(xT(t),yT(t),zT(t))为该点在目标坐标系中的坐标,(xR(t),yR(t),zR(t))为目标点迹在雷达坐标系中的坐标,P为雷达坐标系到目标坐标系的变换矩阵,详细定义见文献[13]。
为了将目标运动相对雷达运动等价为雷达视线在目标坐标系中的姿态角变化,还需将上述直角坐标转化为极坐标形式,即
(5)
其中:
(6)
将三种航迹进行姿态解算,即按照上述过程先获取目标机动的直角坐标,再依据式(5)进行转换,可得三种航迹的方位角和俯仰角随时间变化情况分别如图5。
1.3.2动态RCS计算
本文借助电磁仿真软件FEKO对目标动态RCS进行计算,通过其中的EditFEKO环节编程可对解算姿态角进行实时仿真,具体操作如图6。

图6 动态RCS计算流程
Fig.6 Path of dynamic RCS calculation
首先对目标进行CAD建模,常用的建模方式有CADFEKO,XPATCH等。再将模型导入FEKO进行求解设置,主要包括频率、极化方式、算法选择等。最后再借助EitFEKO脚本编辑器读取所解算的姿态角信息,运行FEKO进行计算。
利用EitFEKO脚本编辑器读取时变姿态角可用以下6行语句表述[14]:
!! for #i =1 to #numangle step num
#theta=FILEREAD("data.txt",#i,1)
#phi=FILEREAD("data.txt",#i,2)
A0:0:0:1:1:0:1:0 #theta:#phi:0
FF:-2
!! Next
其中,#i表示计数变量,#numangle表示姿态角总组数,step num表示设置的步长,#theta表示时变俯仰角,#phi表示时变方位角。!!for与!!Next组合表示循环设置,fileread是读取函数;A0为线极化平面波入射设置函数,FF为计算远场散射函数。
依据上述三种航迹所解算的姿态角对其动态RCS进行计算,所得结果如图7。
2 机动目标探测概率计算方法
2.1 回波幅度推导
为建立目标RCS与回波幅度之间的联系,需先对接收机的基本原理进行分析。图7中,LNA(Low Noise Amplifier)为低噪声高频放大器,Pr为接收回波功率,Si为进入匹配滤波环节的信号功率,So匹配滤波之后的输出功率。匹配滤波后进行包络检波和门限判别,判断是否存在目标[15]。

图8 接收机基本原理
Fig.8 Principle of receiver
设雷达发射功率为Pt,雷达天线增益为G,目标雷达散射截面σ,λ为波长,L为损耗因子,可得回波功率表达式为
(7)
取LNA的增益为GL,则经过低噪声高频放大器后的信号功率为:
Si=PrGL
(8)
此外,Si还可表示为:
(9)
其中,k为波尔兹曼常数,取值为1.38×10-23J/K,T0为标准室温,取值为290 K,Bn为噪声带宽,Fn为噪声系数,No为匹配滤波之后的输出噪声功率。
而匹配滤波后输出的信号噪声功率比可表示为:
(10)
依据文献[6]的归一化定义式,设定A为目标信号与噪声混合信号的幅度,则
(11)
结合上式可得幅度A满足式
(12)
当雷达体制确定后,将雷达固有参数视为常量可将上式简化为:
(13)
(14)
2.2 机动目标探测模型
为了计算发现概率,必须统筹分析信号加噪声通过接收机的情况,也就是计算信号加噪声电压超过检测门限的概率。下面就幅度为A的正弦信号加高斯白噪声一起输入到中频滤波器时的情况进行分析:
设信号的频率为中频滤波器的中心频率f0,r为信号加噪声的包络,A为回波幅度电压,σ0为噪声方差,包络检波器输出包络的概率密度函数表示为[16]:
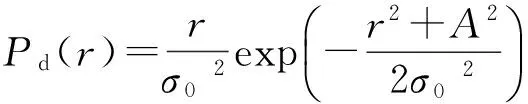
(15)
其中,I0(z)是宗量为z的零阶修正贝塞尔函数,可用式(16)表示:
(16)
设门限电平为UT,噪声包络电压超过门限的概率就是虚警概率Pfa,可由式(17)表示:
(17)
当噪声为高斯白噪声时,由上式可得:
(18)
综上可得发现概率Pd可表示为:
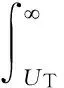
(19)
结合式(19)和式(13)可得:
(20)
3 探测概率仿真及结果分析
依据上述所建探测模型,设置雷达参数,对平飞和俯冲两种典型航迹下雷达对隐身目标的探测概率进行仿真。具体参数设置为:利用FEKO计算动态RCS时将雷达频率f设为1 GHz,发射功率Pt取为400 kW,天线增益G取为30 dB,LNA增益GL取值30 dB,损耗因子L和匹配滤波器噪声系数Fn均取为5 dB,噪声带宽Bn可认为是脉宽的倒数取值1 MHz。当虚警概率为10-6时,两种典型航迹的实时探测概率仿真结果如下。
由图9可以看出,飞机沿着雷达方向平飞时,雷达对飞机目标的探测概率随时间逐渐变大,并从某一时刻起出现明显起伏。这是因为雷达对目标的探测受距离和RCS共同影响。起初飞机距离雷达较远,同时雷达面对的是飞机机头等隐身区域,所以探测概率较小。而当飞机逐渐接近雷达时,机腹等区域暴露,探测概率增大并且随RCS的起伏而出现起伏。
飞机俯冲过程分为三段,如图10所示,本文所设置为0~90 s为进入俯冲段,90~120 s为俯冲阶段,120 s以后退出俯冲。进入俯冲前和退出俯冲后飞机均处于平飞状态,进入俯冲段探测概率不断增大并逐渐出现起伏,退出俯冲段探测概率在起伏中不断减小,分析原理同上。而在俯冲阶段,探测概率起伏剧烈并且出现峰值,这是因为机背和机腹等非隐身区域暴露,RCS剧烈起伏,导致探测概率增大出现峰值并随RCS起伏而剧烈起伏。
实际作战环境下目标机动复杂多变,该航迹以战斗机执行轰炸任务为背景,具体机动动作变换时间点为:0~120 s俯冲机动,120 s以后拐弯折返。由图11可以看出,机动动作的组合导致结果出现了多个相对峰值,发现概率较大的时间段不在集中,而是分散在很长的一个时间段(50~150 s),即进行俯冲与拐弯的阶段。同时,仿真结果的起伏也能得出与单独的平飞与俯冲相同的结论。
4 结论
本文综合考虑影响机动目标探测的主要因素,并以隐身目标为对象,提出了基于目标航迹精确建模及目标动态RCS电磁计算的机动目标探测概率计算方法。该方法克服了传统检测方法对于RCS使用的局限性,在考虑真实目标特性的基础上建立了综合距离量与RCS随机量的机动目标检测模型,相比于传统方法更具合理性。仿真结果表明机动目标探测概率随RCS的起伏而起伏,因此雷达可以利用这种起伏性提高某一瞬时的发现概率而一击命中。但是,由于未对目标滚转机动进行考虑,仿真方法在工程中的应用存在部分局限,因此目标机动的精确模拟是接下来的重点研究方向。
[1]Swerling P. Radar probability of detection for some additional fluctuating target cases[J]. IEEE Transaction on Aerospace and Electronic System, 1997, 33(2):698-709.
[2]杨英科, 李宏, 李文城,等. 目标起伏特性对雷达检飞的试验的影响及应用[J]. 现代雷达, 2013, 35(2): 22-25.
[3]Shnidman D A. Radar detection probability and their calculation[J]. IEEE Transaction on Aerospace and Electronic System, 1995, 31(3): 928-950.
[4]Zhuang Yaqiang, Zhang Chenxin, Zhang Xiaokuan. A novel simulation approach of aircraft dynamic RCS[J]. Progress In Electromagnetics Research M, 2014, 36: 85-91.
[5]Liu J, Fang N, Wang B F, et al. A novel dynamic RCS simulation and analysis method considering attitude perturbation[J]. Journal of Electromagnetic Waves and Application, 2015, 29(14): 1841-1858.
[6]陈世春, 黄沛霖, 姬金祖. 从探测概率的角度评价飞机的隐身性能[J]. 航空学报, 2015, 36(4): 1150-1161.
[7]戴崇, 徐振海, 肖顺平. 非合作目标动态RCS仿真方法[J]. 航空学报, 2014, 35(5): 1374-1384.
[8]晏青, 熊峻江, 游思明. 基于动态RCS的无人机航迹实时规划[J]. 北京航空航天大学学报, 2011, 37(9): 1115-1121.
[9]简康. 无人机航迹规划算法研究[D]. 西安:西安电子科技大学,2014: 28-31.
[10]繆永飞. 军用飞行器航迹规划与显示技术研究[D]. 长沙:国防科技大学, 2006: 35-38.
[11]姬金祖, 束长勇, 黄沛霖. 欧拉角在飞行航迹仿真中的应用[J]. 南京航空航天大学学报, 2014, 46(2): 218-224.
[12]娄寿春. 地空导弹射击指挥控制模型[M]. 北京:国防工业出版社, 2009: 73-75.
[13]黄培康,殷红成,许小剑. 雷达目标特性[M].北京:电子工业出版社, 2005.
[14]戴崇. 雷达目标动态RCS特性建模方法研究[D]. 长沙:国防科技大学, 2013: 39-41.
[15]丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 北京:电子工业出版社, 2013: 219-229.
[16]周品. MATLAB概率论与数理统计[M]. 北京:清华大学出版社, 2012: 2018-220.
