抗强磁干扰滤波器及相移补偿方法

卓美娟，贾方秀，于纪言，殷婷婷，李文彬

(南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094)

0 引言

本文针对此问题，提出了抗强磁干扰滤波器及相移补偿方法。

1 抗强磁干扰滤波设计

利用磁传感器采集地磁信号，期望得到完美的正弦波进行精确的滚转角解算[4]。利用滤波电路进行杂波过滤成为了消除测量误差的手段之一。对于带通滤波器，高阶滤波器由二阶级联而成。二阶带通传递函数为:

(1)

其中，S为低通中复频率；Q=ω0/BW品质因素,BW为带宽。

四阶则由两个二阶传递函数之积组成：

(2)

(3)

(4)

G(S)6=G(S)2G(S)4

(5)

本文以具有低失调、漂移和电压噪声等优点的AD8642作为运算放大器设计了巴特沃斯无限增益多路反馈六阶带通滤波电路。给定系统一个正弦波信号，测量并记录滤波前后的信号信息，如图1所示。

由图1可知，输入信号与输出信号之间产生相位偏移Δx(输出信号为青色曲线)，为了消除相位偏移误差而又不影响输出信号的幅值[5]，在进行滚转角解算时则需要对相位偏移进行建模和补偿。

2 滤波相移补偿方法

2.1 理论相移模型推导

对式(1)、式(2)、式(3)进行傅里叶变换，用jω代替其中的S，得到：

(6)

(7)

(8)

式(6)—式(8)为对应的二阶、四阶分量的频率特性函数，相应的相频函数分别为:

(9)

(10)

(11)

可得，六阶带通滤波器的相频函数为式(9)、式(10)、式(11)的叠加：

(12)

即可得到理论相移特性曲线，如图2中虚线所示。

2.2 对于apFFT的滤波前后实时相位解算

基于理论计算值对实测信号进行相位测量，得到实测值与理论值进行对较。相位测量一般可分为模拟和数字方法两种：传统依靠模拟器件的方法，如二极管鉴相法，脉冲计数法等。测量系统复杂，需专用器件，硬件成本高；近年来，计算机和数字信号处理技术取得长足进步,相位测量逐渐向数字化方向发展[6]。数字化测量的优点在于硬件成本低、适应性强,只需单片机、DSP、FPGA等通用器件就可完成,对于不同的测量对象只需改变程序算法即可,且精度一般高于模拟式测量相位测试测量法[6]。

王兆华教授首次提出全相位傅里叶数字信号处理方法，并验证全相位FFT(简称apFFT)具有“相位不变性”，即使在不同步采样情况下也能得到准确的相位信息[6]。本文采用数采卡采集各频率标准正弦信号滤波前后的信号值进行apFFT变换，得到相位值，再将滤波前后的相位进行比较，来计算实测相位偏移。

2.2.1全相位FFT测相原理数据输入处理[7-8]

全相位数字信号处理中，DFT截取x(n)一段有限长的信号周期序列，对该截断信号进行周期延拓[9]。取N=3,则所有分段的输入输出关系如图3所示。相当于用卷积窗wc对以x(n)为中心，长为2N-1的数据向量x=[x(n+N-1),x(n+N-2),…,x(n),…,x(n-N+1)]T进行加权处理，移位相加形成[9]。

2.2.2传统FFT与apFFT对比分析

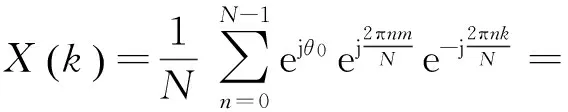
(13)

对x(n)进行apFFT变换，对于时间轴上一点x(0)，存在且只存在N个包含该点的N维向量：

x0=[x(0),x(1),…,x(N-1)]T
x1=[x(-1),x(0),…,x(N-2)]T
⋮
xN-1=[x(-N+1),x(-N+2),…,x(0)]T

(14)

将以上向量进行循环移位，把x(0)移到第一项，得到新的向量：

x0′=[x(0),x(1),…,x(N-1)]T
x1′=[x(0),x(1),…,x(-1)]T
⋮
xN-1′=[x(0),x(-N+1),…,x(-1)]T

(15)

相加后得到全相位向量：

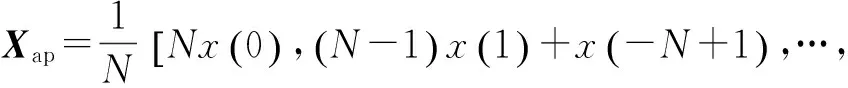
(16)

对式(14)、式(15)进行傅里叶变换，得到：

Xi(k)=DFT[xi]

(17)

Xi′(k)=DFT[xi′]

(18)

(19)

apFFT的输出为：

(20)

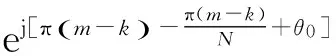
3 仿真验证及分析

基于apFFT相位不变性原理，对实时测量信号采集后用matlab实现apFFT信号处理，同时进行仿真验证，实测相位偏移如图4曲线2所示。曲线6为Multisim软件仿真得到。理论计算值与仿真值重合，与实测值有较小的偏差，可以认为是元器件非线性因素导致。

巴特沃斯带通滤波器的相频特性为非线性函数，为了保证弹载计算机的解算速率，将相移补偿模型简化成多段线性函数。采用最小二乘法进行多段线性拟合[10]。

从而得到多段拟合函数如下：

多段线性函数拟合曲线如图4所示。可见通过六段拟合可以较好地拟合出巴特沃斯滤波器的相频特性曲线。

4 结果与讨论

本文提出了抗强磁干扰滤波器及相移补偿方法，该方法是针对地磁测量系统从信号的时域特性出发的处理方法,在有效保持有用的微弱的地磁信号的同时,还具有计算简单、应用方便的特点,将其应用在地磁探测数据的处理上可以取得较精确结果。仿真验证表明，该相移补偿方法有效地消除了输出信号与输入信号之间的相位误差，保证了解算精度。

关于对相移补偿实现工程化应用则还需要对相位延迟的参数进行标定等一系列工作，本文只是针对数据的后处理进行,若要将这一方法应用到实时的信号处理中去,还需要作更为深入的研究。

[1]晏登洋. 惯性/地磁组合导航技术研究 [D]. 西安：西北工业大学, 2007.

[3]杨云涛, 石志勇, 关贞珍, 等. 一种基于磁偶极子磁场分布理论的磁场干扰补偿方法 [J]. 兵工学报, 2008(12): 1485-91.

[4]高峰, 张合. 基于基准角和补偿角的常规弹药滚转角磁探测算法研究[J]. 探测与控制学报, 2008, 30(5): 11-16.

[5]李伟锋, 封燕芳. 相位补偿电路在有源滤波电路中的应用[J]. 成组技术与生产现代化, 2013, 30(1): 59-62.

[6]王兆华, 黄翔东, 杨尉. 全相位FFT相位测量法[J]. 世界科技研究与发展, 2007, 29(4): 28-32.

[7]贾方秀, 丁振良, 袁峰, 等. 基于全相位快速傅里叶变换谱分析的激光动态目标实时测距系统 [J]. 光学学报, 2010(10): 2928-2934.

[8]肖瑛, 冯长建. 组合窗函数的短时傅里叶变换时频表示方法[J]. 探测与控制学报, 2010,32(3): 43-50.

[9]黄翔东. 全相位数字信号处理 [D]. 天津：天津大学, 2007.

[10]姚雨林. 高旋弹丸滚转角磁测量的系统与滤波设计 [D]. 南京：南京理工大学, 2016.