基于蜂群算法优化向量机的微弱信号检测方法

陈 伟，吕文华，行鸿彦

(1.南京信息工程大学江苏省气象灾害预报预警与评估协同创新中心，江苏 南京 210044；2.南京信息工程大学江苏省气象探测与信息处理重点实验室，江苏 南京 210044；3.中国气象局气象探测中心，北京 100081)

0 引言

混沌是由非线性确定系统产生的不规则运动。通常把雷达映照在海面上后散射的返回波称作海杂波。伴随着海浪里面机理科研的进步，人们发觉海杂波具备混沌的特征[1]。因为遭到变化多端的环境的干扰，雷达接收的信号数据包含有噪声的特征。混沌原理与其他学科的相互交错，让混沌特征和微弱信号检测方面的结合得到了广泛应用，使海杂波背景中微弱信号的检测成为信号检测的热点之一[2]。海杂波信号的去噪分析与海杂波背景下的微弱信号检测具有重大价值，可以提升海面监察能力，故而得到海内外学者的高度重视。因此，对混沌背景中的微弱信号检测问题进行研究拥有极其重大的意义[3]。

以往人们都采用传统的统计方法处理信号，大多基于随机理论，但这些方法并不能体现混沌信号的内在物理特性，且各个模型都有其适用范围，不具有普适性。近年来，统计学习理论已成为预测学习的最佳理论，在其基础上发展了一种新的学习方法-支持向量机(Support Vector Machine，SVM)。支持向量机使用了结构风险最小化原则，可以对各类混沌系统形成不错的预测效果，基于SVM的微弱信号检测给混沌背景中的微弱目标检测提供了新思路。国外方面，1995年，Haykin和Li[1]吸收混沌背景的相关知识，通过神经网络建立了非线性预测模型，并在预测误差中检测信号，成功引入了预测模型检测方法。1997年，Mukherjee等[4]把支持向量机引入到混沌时间序列预测中，其更佳的预测性能让研究又进一步。2009年，Kurian等[5]利用重构动态特性与混沌同步方法对微弱目标信号进行评估和检测，让相空间重构在信号检测领域奠定了理论基础。在国内，2002年，李士心和刘鲁源[6]提出了基于小波阈值去噪方法的研究，系统全面的解析了小波的软阈值去噪、硬阈值去噪、garrote阈值去噪以及semisoft阈值去噪四种阈值去噪方法，为以后的去噪研究提供了基础。2005年，崔万照等[7]利用相空间理论与SVM对混沌时间序列进行了预测，预测模型取得了比较好的预测结果，说明了这个方法的实用性;2006年，高飞和童恒庆[8]在研究含有噪声的Lorenz混沌系统时，引进粒子群算法对其参数进行了估计，从而削减了噪声。2010年，金天力[9]提出了基于对偶约束最小二乘支持向量机的微弱信号检测，通过改变等式约束[10]和损失函数提高了收敛速度，但此方法有一定局限性，预测精度也不够高。

支持向量机中的惩罚系数和核函数参数的优化设置将直接影响预测的精度和效果[11]。传统的参数优化设置容易限于局部最优，并且没有较快的收敛速度，从而影响了模型整体的检测能力和预测精度。本文针对此问题，引进了蜂群算法[12]来优化支持向量机的两个参数,提出了基于蜂群算法优化向量机的微弱信号检测方法。

1 相空间重构理论和支持向量机算法

1.1 相空间重构理论

一般来讲，在非线性系统中的相空间拥有无穷无尽的维数，每个维数的值都难以确定[3]。从非线性系统里[9]，获得一个时间间隔为△t的单变量时间序列{x1,x2,…,xn}，其中：

xj=x(tj),tj=t0+j△t,j=1,2,…,N

(1)

Takens的相空间重构的时间延迟坐标法为混沌系统单变量观测值重构奠定了数学基础[9]。相空间重构的高维映射实现与支持向量机的基本思想相似，都是将输入空间的向量拓展到高维空间，进而挖掘系统蕴藏的信息与规律，重构出原系统模型[13]。对于观测序列(1)，假设它的嵌入维是DE、重构时间延迟是τ，那么重构出的Nm个DE维矢量为Y=[xj,xj+τ,xj+2τ,xj+(DE-1)τ],j=1,2,···,Nm,Nm=N-(DE-1)τ.，对于延迟时间τ与嵌入维DE，一种认为两者不相关，有求DE的遗传编程(Grassberger-Procaccia，GP)算法、伪最临近点法与它的改进形式Cao方法等。另一种认为相关，像C-C法以及它的改进方法等。Takens[13]理论提出，相空间轨迹里的每一点拥有映射关系：

xj+DEτ=F([xj,xj+τ,xj+2τ,xj+(DE-1)τ])

(2)

延迟时间τ与嵌入维数DE不可以随意定值，不然会严重干扰重构的相空间质量。本文使用典型的Grassberger与Procaccia提出的GP[14]算法确定嵌入维DE，并用改良的自相关法确定时间延迟τ。

1.2 支持向量机

支持向量机理论[15]是设立在统计学理论的Vapnik-Chervonenkis维理论与结构风险最小原理基础上的，是一个有监督的学习模型。它把训练误差当作优化问题的约束条件，以模型复杂程度与学习能力之间为优化条件，在两者之间寻找最佳折衷，以便可以得到最好的泛化效果。对于给定的一个训练集(xi,yi)，i=1,2,…,l，xi∈Rn，yi∈R，回归估计函数为：

f(x)=ω·φ(x)+b

(3)

其中，ω，x∈Rn，b∈R，φ是让训练集映射到一个高维特征空间的非线性映射[16]。

最优化问题为：

(4)

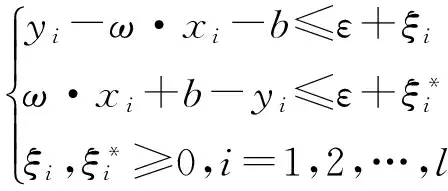
其中，C>0为惩罚因子，是用来在经验风险和模型复杂度之间进行折衷。ξ和ξ*是松弛变量，ε为引进的不敏感损失参数。为了可以处理上面描述的二次规划难题，采用Lagrange乘子法求解，最后得到SVM回归模型为：

(5)

其中，K(xi,x)=φ(xi)·φ(x)为满足Mercer[16]的核函数，这里采用径向基核函数K(xi,x)=exp(||xi-x||2/σ2)。SVM主要参数惩罚因子C和核函数参数σ对SVM的学习和泛化能力影响很大，如何选择最佳匹配的惩罚因子C和核函数参数σ是取得好的回归预测效果的重要一步[13]。本文涉及到的惩罚因子C和径向基核函数参数σ是通过蜂群算法(Artifical Bee Colony，ABC)来最优选择的。

2 基于蜂群算法优化SVM的微弱信号检测方法

泛化能力是衡量预测模型的关键指标，SVM的泛化性能主要与惩罚系数C和核函数参数σ有关[16]。蜂群算法是人们模仿蜜蜂行为而创造的一种优化算法，是智能思想的一种体现。蜂群算法的主要特征是没必要清楚问题的特定信息，仅要求对问题进行优劣的对比。人工蜂的个体通过局部寻优，把全局最优值在群体中突显出来。人工蜂[17]一直保持着较快的收敛速度，并持续到寻优结束。通过蜂群算法可以快速的优化支持向量机中的两个参数，进而消除以往支持向量机模型参数依靠经验确定的弊端，提高向量机的泛化能力。然后，使用优化后的参数进行建模和预测，进而从预测误差中检测出微弱目标信号。

2.1 寻优过程

人工蜂群算法里，蜂群寻找食物源的过程就是寻找待优化问题最优解的过程，而食物源就是待优化问题解空间中的点。换言之，每个食物源对应问题的一个解，食物源的质量对应优化问题的适应度，适应度越高，该食物源的质量越优，也就是该食物源的收益率越高，所对应的解最优。

在基本蜂群算法中，人工蜂群包含3种个体：雇佣蜂、观察蜂和侦查蜂，每个雇佣蜂对应一个确定的蜜源(解向量)并在迭代中对蜜源的邻域进行搜索。根据蜜源丰富程度(适应值的大小)采用轮盘赌的方式雇佣观察峰采蜜(搜索新蜜源)。如果蜜源多次更新没有改进，则放弃该蜜源，雇佣蜂转为侦查蜂随机搜索新蜜源。

初始化时，随机产生SN个可行解(等于雇佣蜂的数目)并且计算适应度函数值。随机产生可行解的公式如下：

xmn=xmin,n+rand(0,1)(xmax,n-xmin,n)

(6)

式中，xmn(m=1,2,…,SN;n=1,2,…,D)为D维向量，D为优化参数的个数。

蜜蜂记录自己到目前为止的最优值，并在当前蜜源邻域内展开搜索，基本ABC在蜜源附近搜索新蜜源的公式为：

vmn=xmn+φmn(xmn-xkn)

(7)

式中，m∈{1,2,…,SN},n∈{1,2,…,D}，K为随机生成且K不等于m，φmn为[-1，1]之间的随机数。算法将新生成的可能解与原来的解作对比，并且使用贪婪选择方法保存较好的解。每一个观察蜂根据概率选取一个蜜源，概率公式为：

(8)

式中，x是蜜源的适应值，fit(xm)是第m个解的适应值对应蜜源的丰富程度，蜜源越丰富，被观察蜂选择的概率就越大。为了避免算法陷入局部最优，当全体采蜜蜂与观察蜂都搜索完全部搜索空间时，假如某个蜜源的适应值在给定的步骤内(本文控制参数“limit”选为50)没有被提升，那么就丢弃该蜜源。而和该蜜源相对应的采蜂蜜变成侦查蜂，侦查蜂使用以下公式搜索新的可能解。

(9)

2.2 时间复杂度分析与对比

蜂群算法的时间复杂度与种群数量、迭代次数等相关。根据上文，SN表示种群数量，limit表示最大迭代次数，x为蜜源的适应值，求解时间复杂度函数为O(f)，那么ABC算法的时间复杂度为O(limit*x*SN)。ABC算法的时间复杂度并不是很小，但是其收敛速度却仅次于遗传算法。遗传算法虽然时间复杂度较小，但随着所遇问题维数的增加，遗传算法对其参数的要求也越来越严格，参数不当就会导致其无法收敛。ABC算法却没有这些问题，只要给ABC算法足够的评估次数，ABC都能较好较快收敛于全局最优解。与蜂群算法类似的蚁群算法虽然也有不错的问题处理能力和收敛速度，但因其时间复杂度较大，因此需要较多的运行时间，远不如蜂群算法理想。

2.3 ABC-SVM主要流程

ABC-SVM预测方法流程图如图1所示。

主要步骤如下：

步骤1 选定试验所需要的个体，把相空间重构后的序列作为向量机的输入序列，输入向量机进行建模、训练并完成预测。SVM中的核函数采用径向基核函数。由惩罚因子C与核函数参数σ组成ABC蜂群算法的个体，构造初始种群。

步骤2 初始化参数，计算个体适应度值。本文选择均方误差的倒数表示适应度值，适应度函数定义为：

(10)

其中，L是数据长度，T(i)是真实值，G(i)是预测值。

步骤3 根据适应度值更新蜜源，不断优化SVM的惩罚因子C和核函数参数σ，使它们达到最优。

步骤4 把优化后的SVM参数带入SVM预测模型，进行相空间重构和单步预测，获得最佳预测结果。

步骤5 计算单步误差，对预测误差进行频谱分析与门限比较，并从中判断是否存在微弱信号，从而实现混沌背景下微弱信号的检测。

3 仿真实验

为了证明ABC-SVM预测方法的有效性，本文进行了三个仿真实验。实验1与实验2均使用典型的Lorenz系统作为混沌背景噪声进行研究，分别在其中加入瞬态信号与周期信号，然后进行建模训练预测，研究预测精度和检测门限。实验3采用雷达实测的海杂波数据作为混沌噪声，验证预测方法的检测精度。将预测均方根误差作为衡量该预测模型的整体预测效果的性能指标，使用信噪比值来衡量该模型检测微弱信号的能力。

实验1 Lorenz系统的迭代方程为：

(11)

式中，α=10，ρ=25，β=8/3。假定初始条件x0=7,y0=4,z0=10，利用四阶龙格-库塔法求解方程，步长为0.01，待系统完全进入混沌状态后，取其中的2 000个数据作为实验室数据进行仿真研究。前1 000个数据作为训练集，用来建立预测模型。后1 000个数据作为验证集，用来验证模型的有效性。利用嵌入维数5和时间延迟1进行相空间重构。

在预测集的第505～554个点处加入幅值为0.000 000 15，长度为50的微弱信号，将微弱信号叠加到Lorenz仿真系统中，作为预测对象。信噪比(Signal to Noise Ratio，SNR)达到-153.936 9 dB，归一化后进行相空间重构和ABC-SVM单步预测，得到的最优参数为C=14.947 9，σ=0.004 220 3，反归一化后，预测结果的均方根误差(Root Mean Squared Error，RMSE)为0.000 047 592。图2为检测结果，有图2(b)可知，样本点n=505～554的误差明显偏大，这与加入微弱信号的位置一致，所以可以确认得到的误差为微弱信号。与传统的SVM方法和径向基函数(Radial Basis Function，RBF)神经网络方法相比，本文使用的模型的检测能力提升了很多，如表1所示。

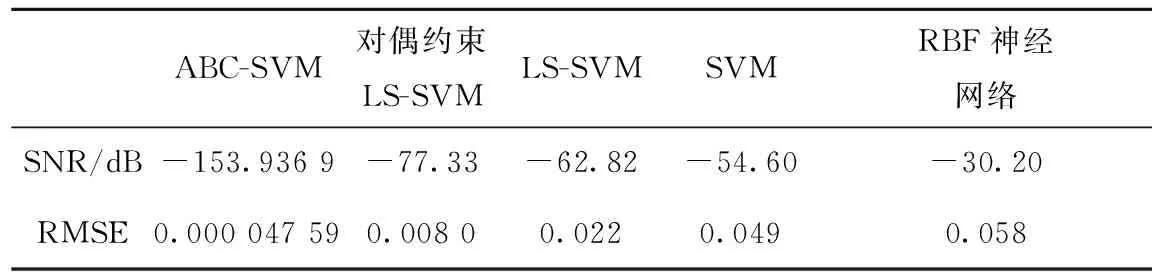
ABC-SVM对偶约束LS-SVMLS-SVMSVMRBF神经网络SNR/dB-153.9369-77.33-62.82-54.60-30.20RMSE0.000047590.00800.0220.0490.058

实验2 对微弱周期信号进行检测，目标信号定义为：

s(n)=0.000 25sin(2πfn)

(12)

归一化频率f为0.01，把周期信号加入到Lorenz混沌背景噪声中，按照实验1的步骤进行检测，信噪比为-89.5 dB，得到的最优参数为C=236.548 3，σ=0.042 771，得到单步预测误差。在预测误差中，可以检测出混沌背景中微弱周期信号的频谱特性。因为从单步预测误差中不能明确信号的确切方位，这里必须对单步误差进行快速傅里叶变换。图3(a)是没有微弱信号时的混沌背景噪声的频谱图。从图3(b)的预测误差频谱图能够看到，归一化频率在f=0.01处频谱出现峰值，因此能够肯定有微弱信号的存在。对数据进行反归一化处理，得到的RMSE为0.000 072 874。与文献[11]的RMSE(0.022)相比，模型的误差有较大提高。从图3(b)中还能够看到，在其他频率处也出现了一些峰值，这是预测自身的误差和在预测的整个系统中受到引入的小信号干扰所造成的。

实验3 本实验使用加拿大McMaster大学的IPIX海杂波数据进行仿真分析。它采用的雷达工作频率是9.39 GHz，天线高度是30 m，天线增益为45.7 dB，每个距离单元的数据包含131 072个采样点，采用VV极化方式。

这次实验首先选取不存在小目标的海杂波数据。拿出前面1 000个点作为训练的样本数据，后面的1 000个点作为预测的样本数据，并用它们进行相空间重构与ABC-SVM单步预测。实验仿真结果如图4(a)所示。接着用含有目标的海杂波数据进行实验，同样选用1 000个点作为训练的样本数据，后面的1 000个点作为预测的样本数据，ABC算法优化的最优参数为C=6.408 1，σ=0.088 95，得到的均方误差为0.000 066 649 7，比文献[18]的均方误差0.013 7降低了三个数量级。图4(b)呈现的误差幅值包含着鲜明的谐波特性，对预测误差进行频谱分析获得图4(c)的误差频谱图。从图4(c)能够看出，归一化频率在0.016附近出现鲜明的峰值，这表明该预测模型可以检测到混沌背景噪声中包含的微弱信号，并且对海杂波微弱信号拥有较强的敏感性。

4 结论

本文提出了基于蜂群算法优化支持向量机的微弱信号检测方法。该方法通过混沌信号的时间延迟和嵌入维实现相空间重构，利用蜂群算法对支持向量机的惩罚系数和核函数参数进行优化，结合支持向量机建立混沌序列的单步预测模型，从预测误差中检测淹没在混沌背景中的微弱信号。通过Lorenz混沌系统与雷达实测的海杂波数据进行仿真分析，利用均方差误差来判断预测性能效果，并与其它方法进行对比。仿真实验结果表明，该方法可以有效的检测出混沌背景中的微弱信号。与传统的神经网络方法和SVM方法相比，该方法拥有较低的检测门限与预测误差，其精度、可行性、泛化能力都有了显著性的提升。本文不足之处是没有考虑背景噪声中混有高斯白噪声的情况，下面的工作就是研究该预测模型对上述情况的微弱信号检测能力。

[1]Haykin S, Li X B. Detection of signals in chaos[J]. Proceedings of the IEEE,1995, 83(1) : 95-122.

[2]郑红利, 行鸿彦, 徐伟. 混沌背景中微弱信号检测的回声状态网络方法[J]. 信号处理, 2015, 31(3) :336-345.

[3]行鸿彦, 徐伟. 混沌背景中微弱信号检测的神经网络方法[J]. 物理学报, 2007, 56(7) : 3771-3776.

[4]Mukherjee S, Osuna E, Girosi F. Nonlinear prediction of chaotic time series using a support vector machine[J]. Proceedings of the IEEE Workshop on Neural Networks for Signal Processing. 1997(7): 511-512.

[5]Kurian A P, Leung H. Weak signal estimation in chaotic clutter using model-based coupled synchronization[J]. IEEE Transactions on Circuits and Systems-I, 2009, 56(4) : 820-828.

[6]李士心, 刘鲁源. 基于小波阀值去噪方法的研究[J], 仪器仪表学报, 2002, 23(3): 478-479.

[7]崔万照,，朱长纯，保文星，等. 混沌时间序列的支持向量机预测[J]. 物理学报，2004, 53(10) : 3303-3310.

[8]高飞,童恒庆. 基于改进粒子群优化算法的混沌系数参数估计方法[J]. 物理学报, 2006, 55(2) : 577-582.

[9]行鸿彦, 金天力. 基于对偶约束最小二乘支持向量机的混沌海杂波背景中的微弱信号检测[J]. 物理学报, 2010, 59(1) : 140-146.

[10]张家树, 肖先赐. 混沌时间序列的Volterra自适应预测[J]. 物理学报, 2000, 49(3) : 403-408.

[11]何建华, 杨宗凯, 王殊. 基于混沌和神经网络的微弱信号探测[J]. 电子学报, 1998, 26(10) : 33-37.

[12]秦全德, 程适, 李丽, 史玉回. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2) : 127-135.

[13]行鸿彦, 郑红利, 徐伟. 基于多参数组合优化的微弱信号检测方法[J]. 探测与控制学报, 2015, 37(1) : 20-26.

[14]Grassberger P, Procaccia I. Measuring the strangeness of strange attractors [J]. Physical D: Nonlinear Phenomena, 1983, 9(1) : 189-208.

[15]Meng Q F, Chen Y H, Peng Y H. Small-time scale network traffic prediction based on a local support vector machine regression model[J]. Chinese Physics B. 2009,18(6) : 2194-2199.

[16]行鸿彦, 张强, 徐伟. 混沌海杂波背景下的微弱信号检测混合算法[J]. 物理学报, 2015, 64(4) : 48-54.

[17]王伟, 龙文. 基于交叉算子的改进人工蜂群算法[J]. 兰州理工大学学报, 2015, 41(1) : 101-106.

[18]王福友, 袁赣南, 谢燕军, 乔相伟. 海杂波的短时非线性预测研究[J]. 雷达科学与技术. 2009, 7(1) : 52-58.