模拟量子自组织神经网络

吴国庆，邴 单，白 静，杜如霞

(南京工业大学浦江学院 基础部，江苏 南京 211134)

1 大脑中的量子力学现象

2 自组织神经网络

自组织神经网络(self organizing map, SOM )是基于人脑中的神经元以下两个特性提出的：(1)神经元之间存在着一种侧抑制现象，当一个神经元细胞兴奋后，它会对周围的其他神经元细胞产生抑制；(2)人大脑的学习方式是一种无导师学习。SOM可以通过一系列的训练，能自动寻找样本数据中内在的规律和本质属性，并且能够在改变网络中的变量和结构的过程中完成自组织和自适应。SOM的结构分为输入层和竞争层，竞争层可以为任意维度的神经网格，如图1所示为一个二维神经网络。

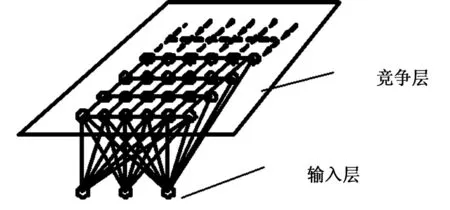
图1 自组织神经网络模型

SOM训练流程大致可以分为四步：(1)接受输入向量，使用判别函数计算各节点函数值；(2)比较判别函数值，选择一个有最大(最小)函数输出值的神经元；(3)激励被选出的神经元和其最接近的神经元；(4)更新被激励的神经元的各项参数，从而增加其对应于特定输入向量判别函数值。在上述训练过程中，神经元权值会向判别函数指向的最优化方向调整。比较选择机制完成后，神经元调整方向一般就确定下来了。这种调整方式容易使得神经网络陷入局部最优化。如图2所示，在寻找最低函数值的过程中若从E、F或H点出发，会陷入到局部极小值D或G，而非整体最小值B。

图2 势阱分布图

3 测不准原理应用于自组织神经网络

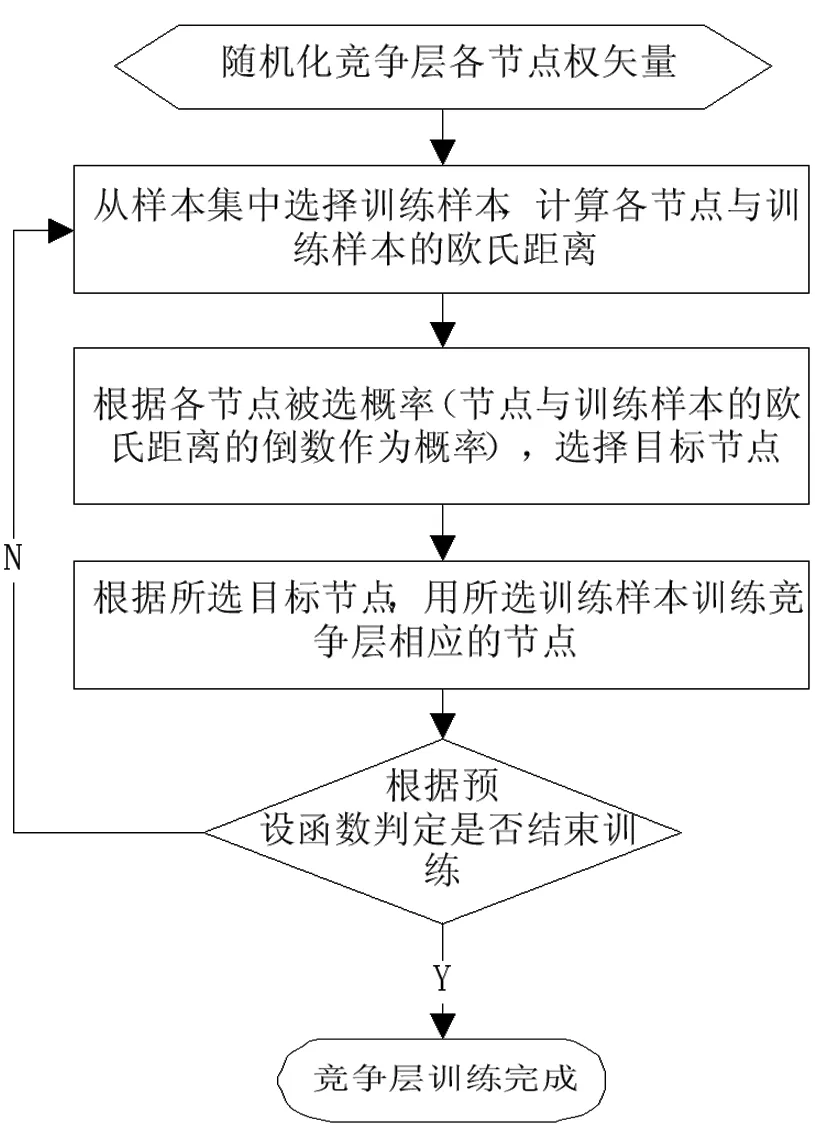
图3 测不准原理应用流程

在经典力学中，若粒子总能量低于势垒大小，则该粒子无法通过势垒。例如图2中能量低于u的粒子很难从F点越过EF势垒到达B或D位置。量子力学中，微观粒子在空间中呈概率分布：能量低于u的粒子若初始情况出现在FH之间的几率最大，该粒子仍有几率出现在AE之间，有机会出现在势能最低点B处。若在SOM训练过程中，将比较判别得到的函数值作为目标神经元被激励的概率，则有可能将训练过程从局部最优化中跳出。测不准原理应用到SOM中得到QSOM(quantum self organizing map)模型，可采用如图3所示流程实现。

在上述流程中样本集各样本与竞争层节点的最小欧氏距离可作为判断结束与否的依据。在SOM中，选择与训练样本欧氏距离最小的竞争层节点作为目标节点，该节点获取激励最大，容易陷入局部最优化。而在QSOM中，与训练样本距离越近，成为目标节点的几率越大，在保证整体趋于优化的同时，减小了陷入局部最优化的概率。

4 模拟测试QSOM

图4 均方差与训练次数关系图

图4中虚线表示模拟训练中MSE随训练次数变化情况，其中虚线表示10次模拟情况，实线表示50次模拟训练平均值。通过上图可以看出网络在250步左右收敛至0.021。相对于螺旋线方程产生的坐标，QSOM填充结果的相对平均误差为7.25%。而测试SOM填充得到的MSE为0.038，平均为误差10.3%，与文献《Non-linear PCA: a missing data approach》中结果近似[4]。

5 结束语

测试结果表明，与SOM相比，QSOM填充质量更好。相较于SOM模型，QSOM模型在训练过程中，由于调整方向增加了不确定性，使得网络更容易跳出局部最优化，其鲁棒性、容错性更强。可应用于处理非线性问题的缺失值填充、预测等。

[1]Maeda M,Suenaga M,Miyajima H.Qubit neuron according to quantum circuit for XOR problem[J]. Applied Mathmatics and Computation,2007,185(2):1015-1025.

[2]Scott Makeig.Event-related brain dynamics[J].TRENDS in Cognitive Sciences,2004,8(5):204-210.

[3]Li P,Chai Y,Xiong Q.Quantum neural modeling: quantum gate structure in Elman networks[C]//Proceeding of Fourth International Workshop on Advanced Computational Intelligence (IWCI).Wuhan:[s.n.],2011:315-320.

[4]Matthias Scholz,Fatma Kaplan.Non-linear PCA:a missing data approach[J]. Bioinformatics,2005,21(20):3887-3895.