带有自寻优调整因子的模糊控制系统设计

张秋颖，龙 松，张文钢



带有自寻优调整因子的模糊控制系统设计

张秋颖，龙 松，张文钢

(武昌首义学院基础科学部，武汉 430064)

提出了一种带有调整因子的模糊控制系统的调整因子自寻优方法，仿真结果表明，此种控制方法与传统PID控制方法相比，在稳定性、快速性和适应性方面均有提高。

模糊数学 模糊控制 调整因子 自寻优

0 引言

自动控制的产生来源于人们对生产过程自动化的需求，既可以减轻人们的劳动强度，又可以提高生产效率和产品质量。随着科学技术的迅猛发展，被控对象变得日益复杂，被控对象的非线性、时变性、不确定性等使得难以建立其精确的数学模型，即使建立了非常复杂的数学模型，也难以用于实际的控制系统设计，这就使得基于被控对象精确数学模型的经典控制理论和现代控制理论受到了严峻的挑战[1]。

面对难以用传统控制理论控制的复杂对象，具有一定操作经验的人员采用人工控制的方法往往能取得满意的控制效果。这些操作人员不需要对象的数学模型，只凭借操作经验，借助简单的仪表对被控对象进行观测和分析，并通过执行机构对被控过程加以调节，从而实现复杂对象的有效控制。智能控制是借助于计算机模拟人对难以建立精确数学模型的复杂对象的智能控制决策行为，基于控制系统的输入输出数据的因果关系推理，实现对复杂对象计算机闭环数字控制的技术。本文研究的模糊控制技术即是智能控制技术的一个重要方向，主要讨论带有自寻优调整因子的模糊控制系统的设计技术。

1 模糊数学和模糊控制

模糊控制系统应用模糊数学的方法模拟人的模糊逻辑思维对未知精确数学模型的被控对象进行控制。其基本组成如图1所示，其中模糊控制器包括模糊化、模糊规则、模糊推理和非模糊化4个模块，广义被控对象包括执行机构和被控对象。

图1 模糊控制系统框图

图中，模糊控制规则模拟了人对被控对象的控制作用，是模糊控制器的核心。模糊集合一般根据习惯确定为：

{负大，负中，负小，零，正小，正中，正大}

或：

{NB，NM，NS，O，PS，PM，PB}

进埔站#1、#2、#3接地变和#1、#2站用变保护装置统一使用351F，351F为由微机实现的数字式保护、测控一体化装置，实现馈电线路的保护，完成遥测、遥信、遥控、遥脉等运动功能。351F采用标准6U（半层）机箱，由交流（WB511）、电源（WB560）、CPU（WB520）、操作（WB540）等4个插件

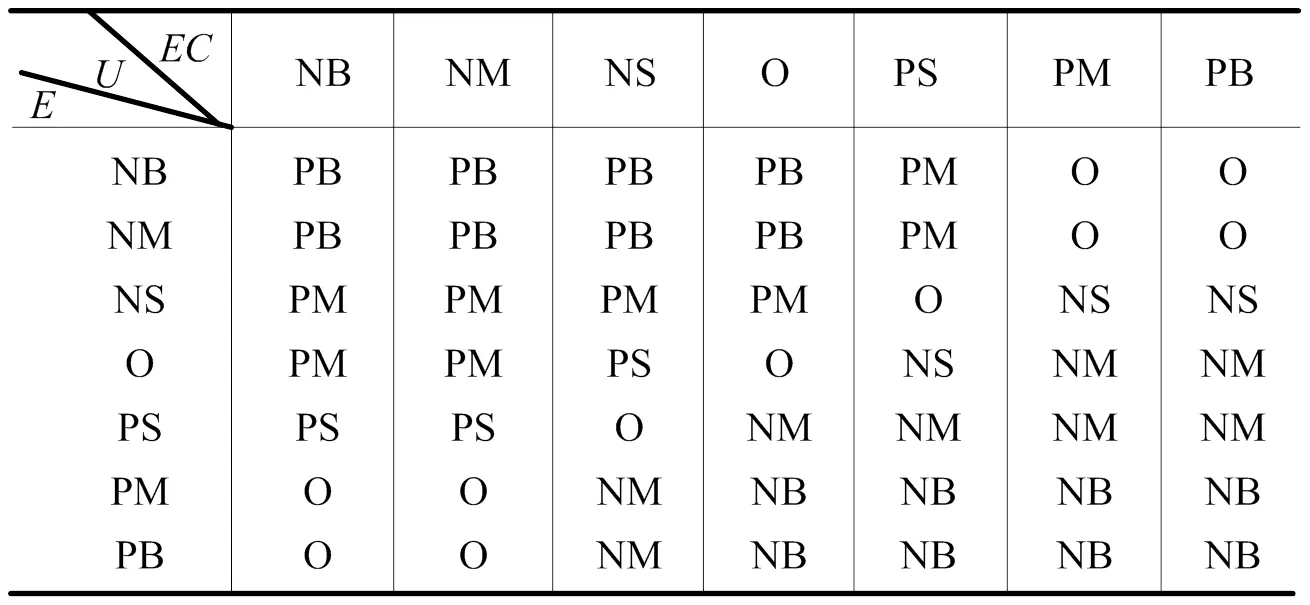
这样，根据人对被控对象的控制方法，得到模糊控制规则表如表1。

图2 模糊控制器信息处理过程

在实际应用中，一般将控制规则结合论域转化为一个控制表，存储在计算机中用于在线控制。若各量论域选择为[-3，3],则根据模糊控制规则表可得模糊控制表如表2。

表1 模糊控制规则表

2 调整因子的自寻优计算方法

表2可写成解析形式：

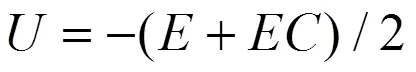
为适应不同被控对象的要求，在式(1)的基础上引进一个调整因子，得到带有调整因子的控制规则：

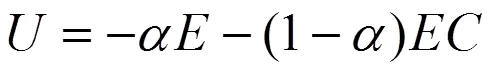
的确定一般是根据经验或实验调试结果，具有一定的盲目性，本文提出一种基于黄金分割法的调整因子自寻优计算方法，步骤如下[3]：

2）设置的寻优区间[0,0]；

3）按下式计算两个寻优点：

4）继续缩小区间，直至b-a≤，得到性能指标最小点α。

黄金分割寻优法的优点是收敛速度快，不要求性能函数可微，且每次迭代只需计算一次函数值，计算量小，程序简单。

3 仿真和对比

实际系统中，被控对象一般是带有滞后的惯性环节，所以选取控制对象传递函数为：

控制系统框图如图3。

表2 模糊控制表

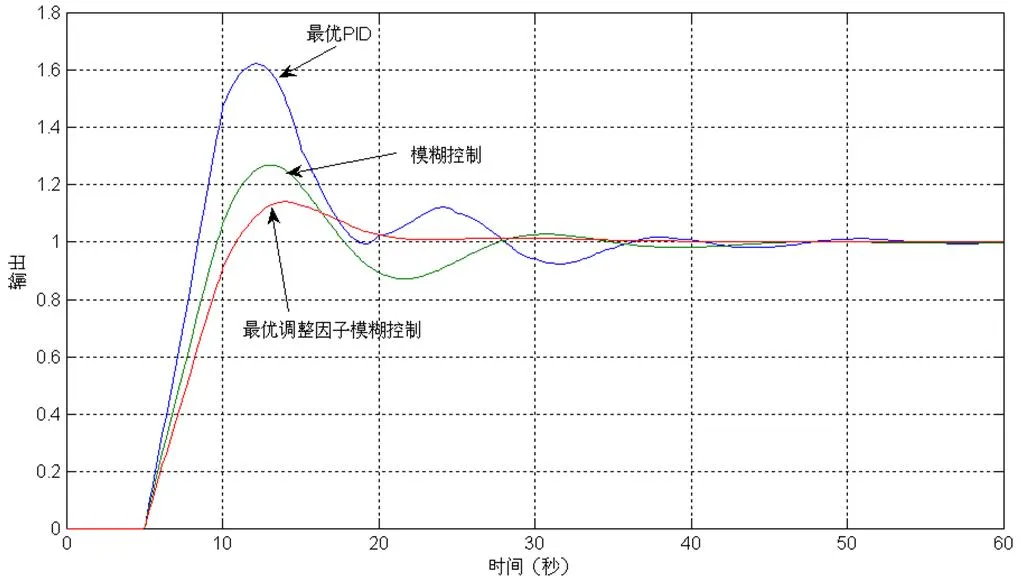
图4 阶跃响应仿真图

为便于对比，图3包括3个控制系统：一是IAE性能指标最优的PID控制系统；二是采用式(1)模糊规则的模糊控制系统；三是采用最优化调整因子的模糊控制系统。其中，为消除模糊控制系统的稳态误差，在模糊控制系统中加入了积分环节。由于采用了黄金分割寻优法，收敛速度较快，在寻优区间为[0，1]、取0.01时，经过8次迭代即可确定α=0.41。

各系统阶跃响应曲线如图4所示，从仿真结果看，模糊控制在响应时间、超调量等方面优于最优PID控制，而带有最优调整因子的模糊控制又优于普通的模糊控制，最优PID控制、普通的模糊控制、最优调整因子的模糊控制的IAE指标分别是11.56、9.72、8.80，也证明了带有最优调整因子的模糊控制的优势。

下面通过改变被控对象传递函数参数验证控制系统的适应性。一是改变被控对象的参数，如式(4),一是改变系统的结构，如式(5)，最优PID控制系统和最优调整因子模糊控制系统的仿真结果如图5、6所示。

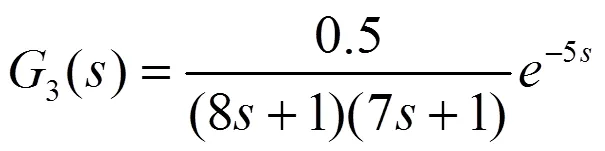
从仿真结果看，基于被控对象准确数学模型的PID控制在被控对象参数和结构的变化后，控制已经不稳定，基本没有适应能力。而带有最优调整因子的模糊控制适应能力较强，在被控对象参数和结构变化后，也能获得较好的控制效果。

图5 参数和结构变化对最优PID控制的影响

图6 参数和结构变化对最优调整因子模糊控制的影响

4 结束语

本文主要研究了带有调整因子的模糊控制系统中调整因子的自寻优方法，并通过仿真对比证明了其准确性和可靠性。此外，还应强调，为了与传统PID控制进行比较，文中给出了被控对象的数学模型，在实际应用中，对于难以获得被控对象精确数学模型的系统，传统控制方法是无能为力的，只有通过模糊控制等智能控制方法才能实现有效控制，这是模糊控制等智能控制相对于传统控制的最大优势。

[1] 李士勇, 李研. 智能控制[M]. 北京: 清华大学出版社, 2016: 3-15

[2] 谢季坚, 刘承平. 模糊数学方法及其应用[M]. 武汉：华中科技大学出版社, 2017: 1-5

[3] 李国勇. 最优控制理论及参数优化[M]. 北京: 国防工业出版社, 2006: 213-218.

Design of Fuzzy Control System with Self-optimizing Adjusting Factor

Zhang Qiuying, Long Song, Zhang Wengang

（Basic Science Ministry of Wuchang Shouyi University, Wuhan 430064, China）

TP273

A

1003-4862（2018）02-0057-04

2017-11-20

张秋颖(1986-)，女，讲师。研究方向：基础数学。zhangqiuyingais@163.com