基于差厚技术的汽车仪表板管梁轻量化设计
2018-03-10徐天爽胡贤磊刘维海
刘 念,徐 涛,徐天爽,胡贤磊,刘维海
(1.吉林大学 机械科学与工程学院,长春 130022;2.东北大学 轧制技术及连轧自动化国家重点实验室,沈阳 110004;3.中国第一汽车股份有限公司 技术中心,长春 130011)
0 引 言
汽车轻量化不仅是实现节能减排的关键技术之一,而且利于减少碰撞时的惯性力,并提高碰撞安全性[1,2],已然成为汽车行业发展的重要方向之一。
轻量化实施策略是在保证车辆性能目标和乘坐品质的前提下,根据各总成或零部件的承载条件逐一优化,最大程度减轻各零部件质量,最终实现整车质量减轻。轻量化相关的新工艺技术可进一步提升传统材料的使用性能,制造出结构更合理,性能更优,满足承载要求的零部件。通过柔性轧制技术发展起来的连续差厚板(Tailor rolled blank,TRB)[3,4]技术可根据不同区域承载特性进行零部件几何形状和材料布局的优化设计,实现节省材料、减轻质量的目标[5]。与激光拼焊技术相比,差厚板在厚度变化位置没有焊缝,在承载时不会出现厚度突变区域应力集中的问题,且生产连续性好、效率高,成本低,在汽车零部件领域应用比例逐步提升。Audi、BMW、GM等汽车企业均已将德国Mubea公司的差厚板车身零部件,如承载梁结构、车身连接件和加强件等)用于汽车产品中[6];东北大学研究了周期变厚度轧制工艺[7]。
汽车仪表板管梁承载支撑人机界面控制所需设备及内饰件,用于保护成员的吸能支架、用于安装仪表及空调的支架、气囊模块支架等结构件均焊接在仪表板管梁上[8]。为应对复杂承载工况,不仅要求管梁与其他结构件之间的焊接质量要好,且强度要高。特别要保证能够承受来自于低阶频率、垂直颠簸、气囊爆破、制动器支架侵入等工况下传递来的冲击载荷。然而,传统的管梁采用等厚度结构设计,这就需要此管梁每一处都以最大承载能力来选择自身的厚度。虽然能够较好地保证支架连接强度,但存在很大的性能冗余问题,难以实现轻量化设计。若直接减薄材料厚度,则会造成整体刚度和模态频率下降。因此引入差厚新工艺制备仪表板管梁,可根据承载需求,合理地布置不同厚度的管梁结构,在保证特定区域强度或刚度要求的情况下,实现以轻量化为目标的优化设计[9]。此类的差厚板管梁结构制备的工艺流程为:根据需求变厚度轧制→退火热处理→辊弯→焊接成管。
本文将差厚板技术应用于仪表板管梁的结构设计中,依据轧制可行性、便利性和成材率,为保证焊接区域强度,避免管梁与支架焊接位置出现在厚度过渡区[10],提出五段式和三段式的差厚板管梁结构最优设计方案。与原等厚度结构对比了低阶频率、垂直颠簸、制动器支架侵入、乘员安全气囊(Passenger airbag,PAB)爆破工况的性能指标,结果表明差厚板技术能够在保证其性能指标的同时大幅减轻质量。利用差厚板技术进行整体仪表板管梁的结构设计是轻量化技术领域的全新尝试,其轻量化效果好,工程应用可行性高。
1 仪表板管梁承载条件及性能指标
图1为某乘用车仪表板管梁骨架示意图。由图1可见,各功能支架均焊接于管梁的特定区域,即除了需考虑管梁自身刚度特性以外,还应校核其他支架动力承载时对管梁的影响。
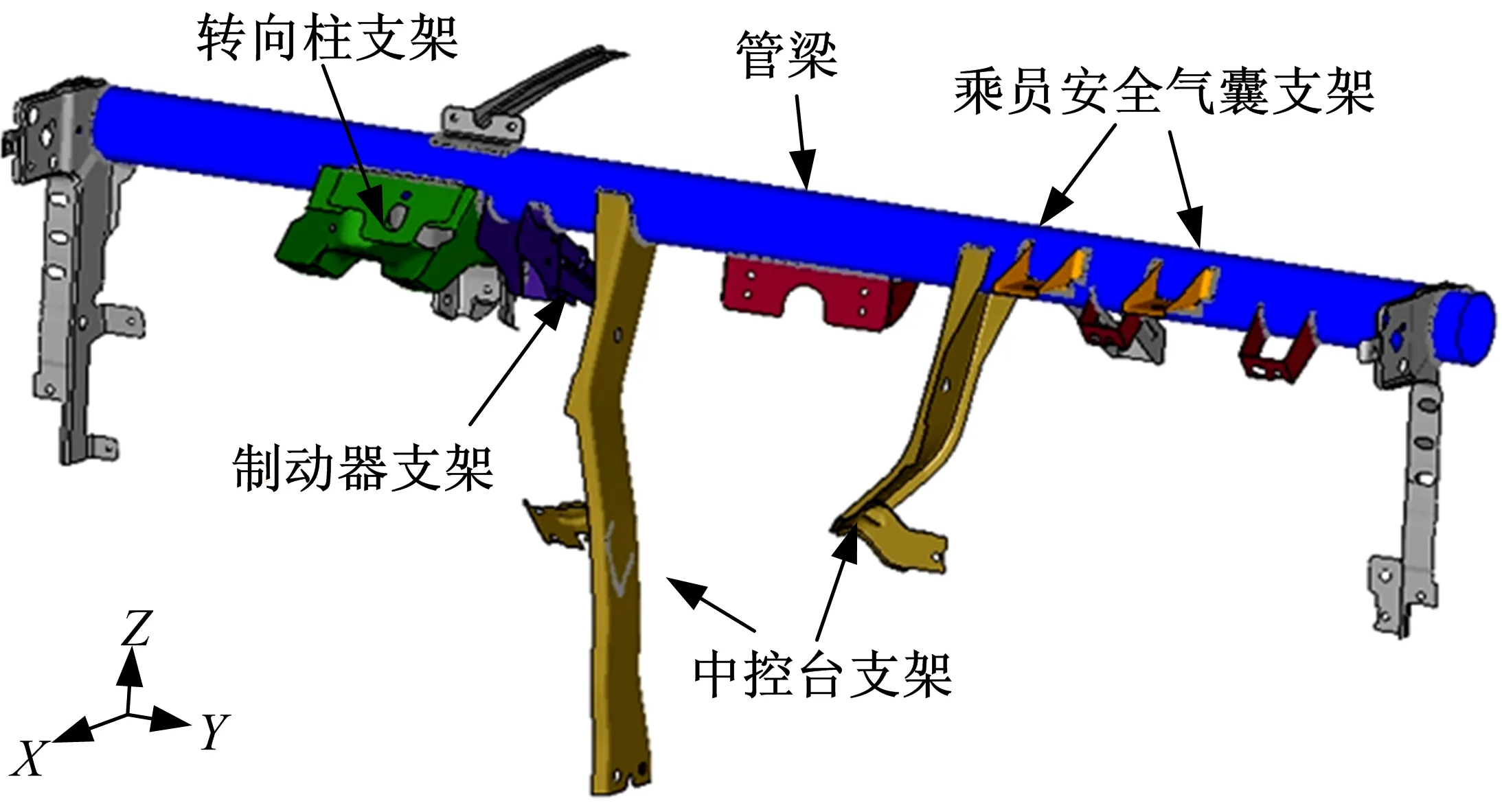
图1 某乘用车的仪表板管梁骨架示意图Fig.1 Schematic diagram of dashboard crossbeam of a passenger vehicle
为避免共振风险,需检核管梁在安装状态下的低阶频率(前四阶)是否达标;垂直颠簸工况用以模拟车辆行驶在较恶劣的路面时,车辆不规则的垂直跳动对仪表板管梁骨架的影响,此种工况会造成管梁与车身的固定区域或与其他支架的焊接区域应力集中,导致管梁局部塑性变形甚至连接失效;制动器支架侵入工况是模拟车辆紧急制动时,驾驶员脚部对制动器踏板施加大载荷过程中对制动器支架及管梁的影响;在发生中速或高速碰撞时,PAB会快速弹出,对PAB固定支架和管梁造成冲击,管梁的相应部位需具备足够的强度以保证不发生塑性变形。表1列出了低阶频率、垂直颠簸、制动器支架侵入和PAB爆破工况的仿真分析边界条件。
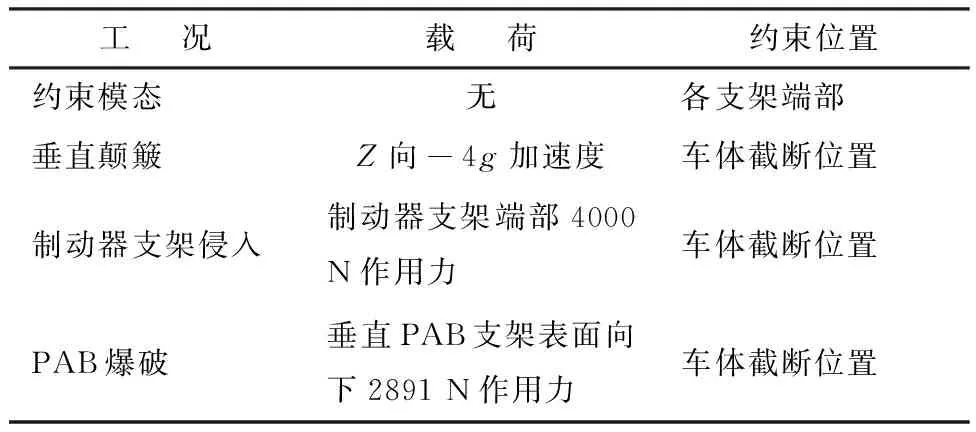
表1 仪表管梁骨架仿真分析边界条件Table 1 Boundary conditions of dashboard cross beam
根据车辆垂直颠簸、制动器支架侵入、PAB爆破工况这3种强度分析工况,建立了车身前部的有限元模型,车体边缘全约束,如图2所示;低阶频率分析仅需要仪表板管梁骨架模型即可,各功能支架与其他附件连接位置做全约束处理。本文将差厚板技术应用于仪表板管梁的轻量化设计中,目的是在保持性能与原等厚度管梁一致的情况下,最大限度地减轻质量,并提出工程化的可行方案。
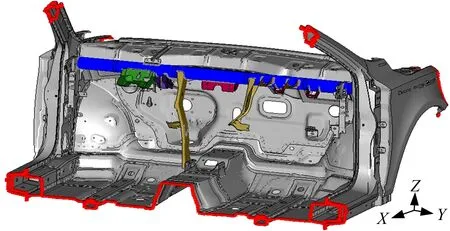
图2 前部车身有限元模型Fig.2 Finite element model model of frontal vehicle body
2 差厚仪表板管梁最优设计
现基于某乘用车提取等厚度管梁结构。结构直径为64 mm,长度为1352 mm,厚度为1.25 mm,质量为6.2 kg。材料为20#钢,屈服强度为245 MPa,抗拉强度为410 MPa。本文综合考虑了差厚板结构特性、制造可行性(轧制条件、轧制便利性)及功能支架焊接位置的影响,分别提出一种五段式和三段式的差厚管梁结构,如图3所示。
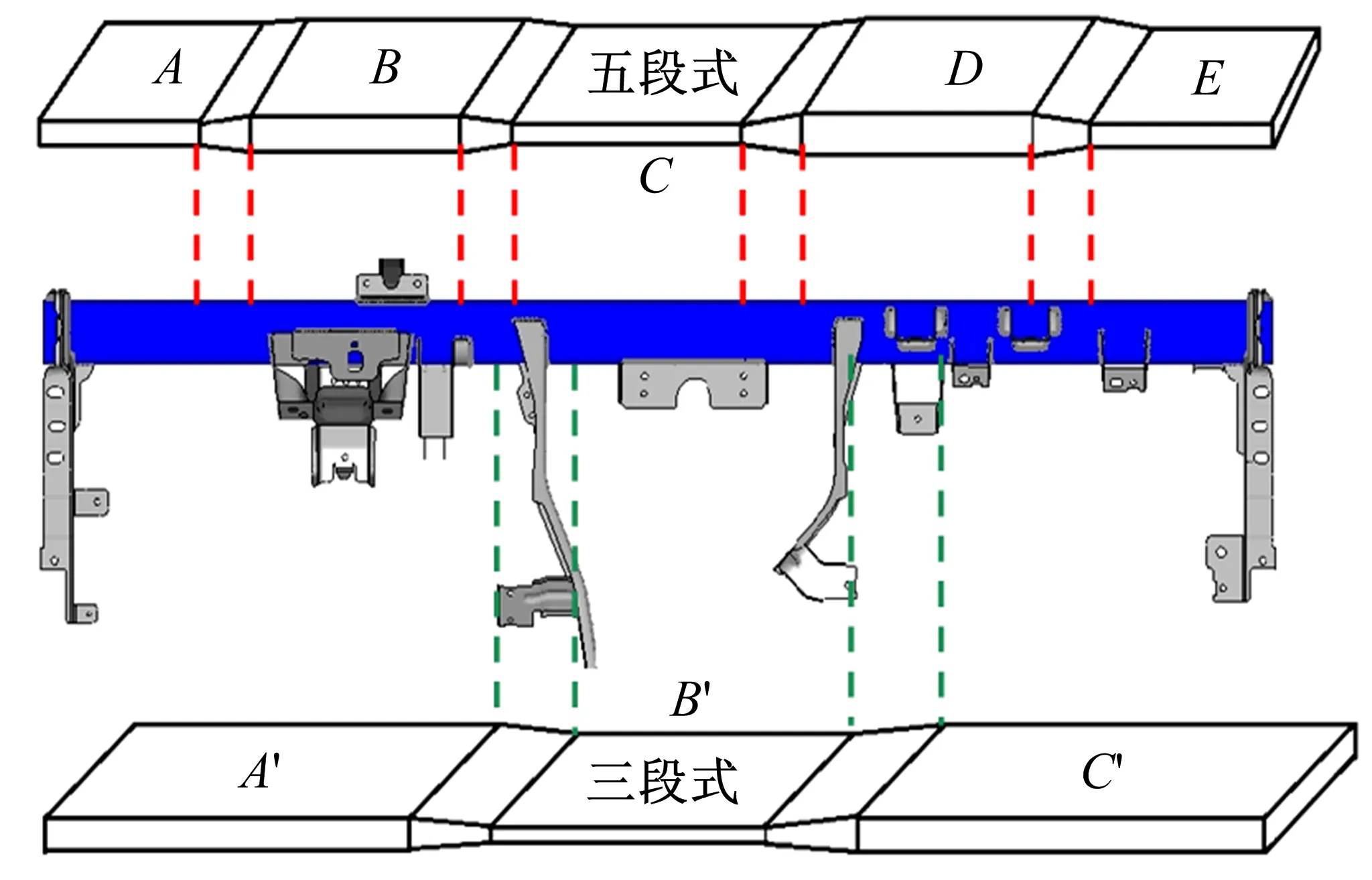
图3 五段式和三段式差厚板示意图Fig.3 Schematic diagram of five segments and threesegments plans of TRB
可见,五段式结构由等厚度薄区A、C、E,以及等厚度厚区B、D组成,薄区与厚区之间由4个过渡区连接;三段式结构由等厚度薄区B′,以及等厚度厚区A′、C′组成,薄区与厚区之间由2个过渡区连接。显然,三段式的优点在于轧制过程中调节轧辊辊缝的次数较少,且支架焊接区域与厚度过渡区更远,有利于保证焊接强度,但降重效果不如五段式。换言之,若更注重于轧制便利性及功能支架焊接位置的影响,应侧重研究三段式差厚结构;若更注重于轻量化效果,则应重点研究五段式差厚结构。在此分段基础上,本文将对这两种差厚方案分别进行优化设计,以获取最佳设计结果。
现建立五段式差厚管梁结构优化问题数学模型。取五段式结构整体质量最小作为优化目标,结构的薄区、厚区和过渡区的厚度作为设计变量。由于与原等厚结构相比,差厚结构的部分区域厚度减薄,这将导致结构整体刚度和模态频率有所下降,因此为了保证刚度特性满足要求,需要控制前四阶频率降幅在2.5%以内,同时限制等厚度区域料厚不超过初始厚度1.25 mm。建立对应的数学模型为:
(1)
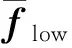
同理,建立三段式差厚管梁结构优化问题数学模型为:
(2)
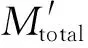
由于支架焊接位置是固定的,因此焊接区域的边界为等厚区与过渡区的分界线处,即优化模型(1)和(2)中的各类厚度区域的长度是定值,而厚度是设计变量。
为获得优化问题(1)(2)的最优解,本文采用一种改进粒子群算法(Particle swarm optimization,PSO)进行求解[11]。该方法是一种多点寻优的群智能优化算法,对问题的连续性不做限制,且无需获得问题的导数信息。其基本原理为:首先随机初始化粒子群,并设定最大迭代次数kmax。随后每次迭代都计算粒子的当前个体极值和全局极值,以此来重新调整粒子的搜索速度和位置,从而实现全局范围内寻优。当迭代次数达到kmax时终止寻优并输出最优解。
采用如下公式更新各粒子的速度和位置:
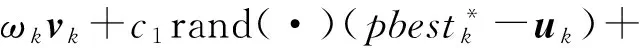
c2rand(·)(gbestk-uk)
(3)
uk+1=uk+vk+1
(4)
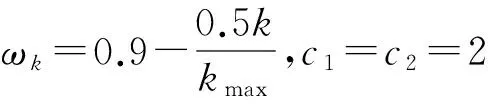

(5)

(6)
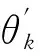
考虑工艺实现,将得到的最优设计变量进行圆整,最优设计方案列于表2中。可见,各方案厚度过渡区的厚度均呈梯度变化,均匀过渡。其中,支架与管梁连接的焊缝均未出现在厚度过渡区,这样就保证了焊接强度。由于厚度过渡区长度较小,为提升建模效率,在仿真分析时将其厚度设置为薄、厚区厚度的均值。与原等厚管梁结构相比,优化得到的两种差厚管梁结构最优设计方案不仅满足约束条件,且均实现了减轻质量的需求,其中五段式方案质量减轻了13.18%,三段式方案质量减轻了8.1%。
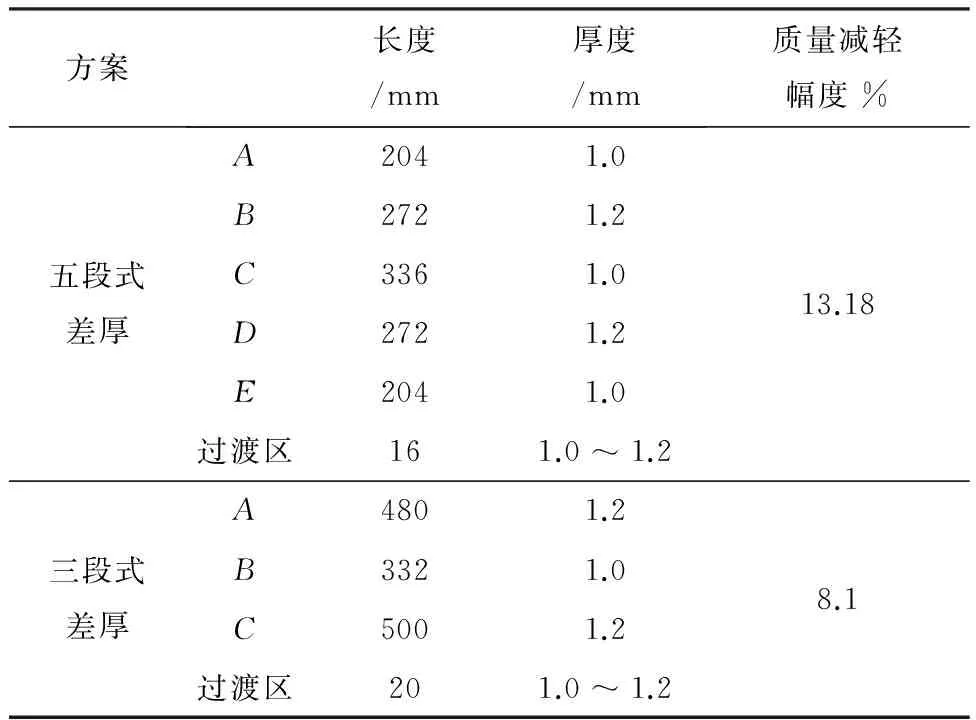
表2 差厚板各方案的几何参数及轻量化效果Table 2 Geometrical parameters and lightweightresults of each TRB plan
3 各差厚设计方案性能分析及对比
3.1 低阶频率分析
考虑仪表板管梁骨架的实际安装状态,即各功能支架末端约束,且管梁两端约束,对各方案进行前四阶约束模态分析,结果列于表3中。
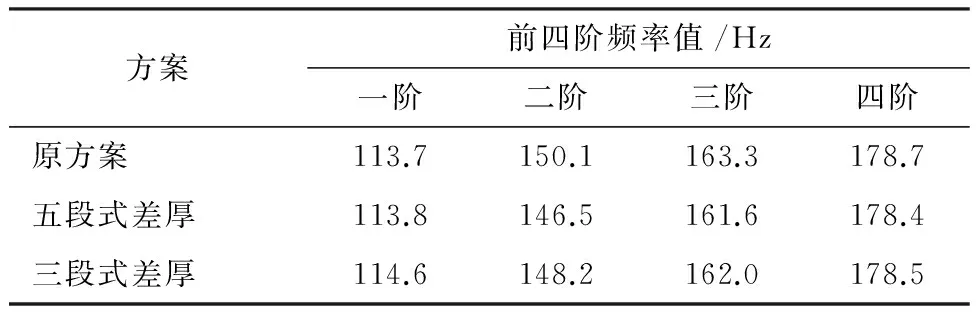
表3 前四阶频率结果对比Table 3 Comparison of frequencies under first four orders
由表3可知,差厚板各方案与原等厚方案前四阶模态频率值相差较小;且通过对比变形动画,可见振型一致。五段式方案的第二阶模态频率比原方案下降2.4%,此为所有方案中的最大降幅;五段式方案和三段式方案的一阶模态频率值略高于原方案。因此,各方案均满足前四阶模态频率分析工况的性能要求。
3.2 强度分析
3.2.1 垂直颠簸工况
垂直颠簸工况要求仪表板管梁不发生塑性变形,即管梁的最大应力值要小于屈服强度。通过对轧制板材实施不同的退火工艺,调整退火时间、温度等因素,可使差厚板获得较为理想的材料特性。通过仿真分析,各方案在此工况下仪表板管梁的最大应力值均未超过材料的屈服强度,即不会出现塑性变形,各方案均满足此工况的性能要求。图4列出了五段式方案的管梁应力分布图,此方案的应力值最大,且应力最大位置出现在转向柱支架焊接处,为93.94 MPa,小于屈服强度(245 MPa)。
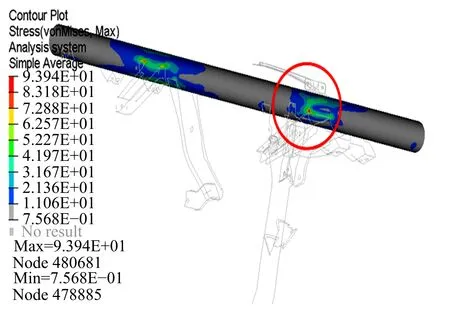
图4 五段式方案在垂直颠簸工况下的应力云图Fig.4 von Mises stress contour of five segmentsplan under vertical bump
3.2.2 制动器支架侵入工况
制动器支架侵入工况模拟的是紧急制动时的大载荷极端工况,需保证仪表板管梁不出现断裂失效的情况,即管梁的最大应力值要小于材料的抗拉强度。对比各方案的仿真分析结果,三段式方案的管梁应力值最大,出现在制动器支架焊接区域,为406.6 MPa,小于材料抗拉强度(410 MPa),即不会发生断裂失效。图5为三段式方案的管梁应力云图。
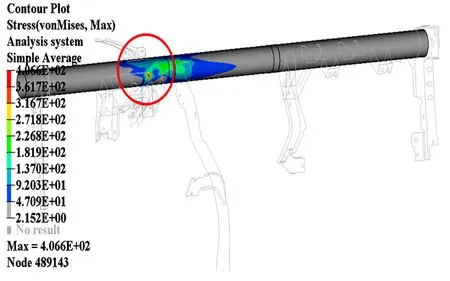
图5 三段式方案在制动器支架侵入工况下的应力云图Fig.5 von Mises stress contour of three segmentsplan under brake force
3.2.3 PAB爆破工况
在车辆发生前部中高速碰撞时,PAB会在瞬间充气膨胀,此时会对2个PAB固定支架及仪表板管梁造成冲击。PAB爆破后需要将气囊模块拆卸并更换,这就要求管梁不应出现塑性变形,但允许支架发生塑性变形,即管梁的最大应力值均小于材料的屈服强度。仿真结果显示,五段式方案中的仪表板管梁最大应力出现在PAB的固定支架焊缝周围,为240.1 MPa,是各方案中的最大值,但仍小于材料的屈服强度(245 MPa),满足管梁的强度要求。图6中列出了五段式方案在此工况下的管梁应力云图。由于本例中仅考虑差厚板管梁强度是否达标,因此各差厚板管梁方案均满足性能要求。
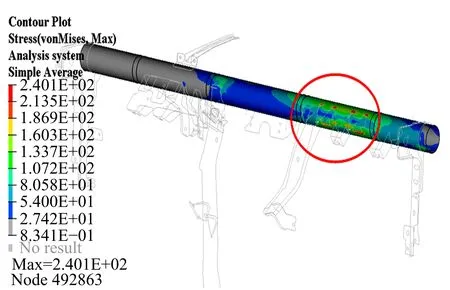
图6 五段式方案在PAB爆破工况下的应力云图Fig.6 von Mises stress contour of five segmentsplan under PAB expands
3.2.4 各方案的强度分析结果汇总及对比
表4列出了各方案在垂直颠簸、制动器支架侵入及PAB爆破上述3种强度分析工况下的结果及相应的性能评价。可见,3种强度分析工况下,虽然各方案分析结果略有差异,但均满足对仪表板管梁和功能支架的强度及刚度要求,因此本文提出的五段式和三段式差厚板管梁方案均能较好地达到性能控制目标。结合表2中质量减轻幅度可知,五段式方案的轻量化效果最优,质量减轻幅度达13.18%,且过渡区距离焊接支架8 mm,对焊接强度不会造成影响,实际生产加工时便于控制。同时,各方案均能满足差厚板轧制工艺,逐步加工成管梁结构。三段式方案的优势在于三段式结构设计更便于轧制及过程控制,但其质量减轻幅度不如五段式,仅为8.1%。
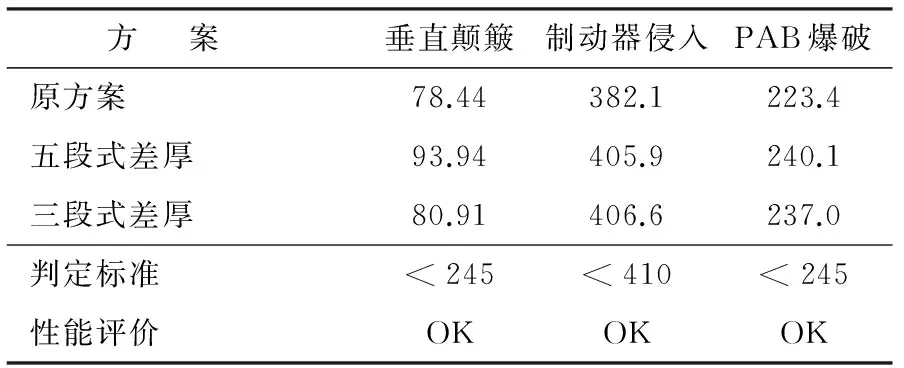
表4 强度分析工况中管梁最大应力对比Table 4 Comparison of maximum stresses for crossbeam strength analysis MPa
综上,若考虑轧制便利性,可选择三段式方案,其制造过程更易控制,但轻量化效果不显著;若从轻量化角度出发,在满足低阶频率和强度要求的条件下,可采用五段式方案,其支架焊接处与厚度过渡区的距离较为适中。
4 结束语
本文根据仪表板管梁的结构特征和承载性能要求,基于差厚技术,分别最优化设计了五段式和三段式的轻量化仪表板管梁结构。通过与原等厚度的管梁结构性能进行仿真对比,验证了这两种差厚板方案均能够满足低阶频率及特定强度特性要求,且轻量化效果显著(质量减轻了约8%~13%)。因此,轧制差厚板技术能够为降低整车质量提供全新的结构方案,特别是对板壳类和薄壁承载梁结构而言,应用前景广阔。
[1] Morteza K, Imtiaz G, Masoud R R, et al. Design of lightweight magnesium car body structure under crash and vibration constraints [J]. Journal of Magnesium and Alloys, 2014, 2(2): 99-108.
[2] 王登峰,卢放. 基于多学科优化设计方法的白车身轻量化[J]. 吉林大学学报:工学版,2015, 45(1): 29-37.
Wang Deng-feng, Lu Fang. Body-in-white lightweight based on multidisciplinary design optimization [J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(1): 29-37.
[3] Liu X H, Wu Z Q, Fang Z. From TRB and LP plate to variable gauge rolling: technology, theory, simulation and experiment [J]. Materials Science Forum, 2012, 706-709(13): 1448-1453.
[4] Zhang Y, Tan J. Numerical simulation and vertical motion control of rolls for variable gauge rolling [J]. Journal of Iron & Steel Research International, 2015, 22(8): 703-708.
[5] Chuang C H, Yang R J, Li G, et al. Multidisciplinary design optimization on vehicle tailor rolled blank design [J]. Struct Multidisc Optim, 2008, 35: 551-560.
[6] Meyer A, Wietbrock B, Hirt G. Increasing of the draw depth using tailor rolled blanks-numerical and experimental analysis [J]. International Journal of Machine Tools & Manufacture, 2008, 48(5): 522-531.
[7] 张广基,刘相华,胡贤磊,等. 变厚度轧制轧件水平速度变化规律[J]. 东北大学学报:自然科学版,2013,34(1):75-79.
Zhang Guang-ji, Liu Xiang-hua, Hu Xian-lei, et al. Research on variation of work piece horizontal velocity for variable gauge rolling [J]. Journal of Northeastern University (Natural Science), 2013, 34(1): 75-79.
[8] 高云凯,刘海立,万党水,等. 挤压镁合金汽车仪表板横梁骨架的设计与分析[J]. 汽车工程,2011,33(2): 167-171.
Gao Yun-kai, Liu Hai-li,Wan Dang-shui, et al. Design and analysis on cross car beam of extruded magnesium alloy [J]. Automotive Engineering, 2011, 33(2): 167-171.
[9] Duan L, Sun G, Cui J,et al. Crashworthiness design of vehicle structure with tailor rolled blank [J]. Struct Multidisc Optim,2016, 53:321-338.
[10] Wang D, Dong L, Liu H, et al. Velocity preset and transitional zone's shape Optimization for tailor rolled blank [J]. Journal of Iron and Steel Research, International, 2015, 22(4): 279-287.
[11] Chen D, Chen J, Jiang H, et al. An improved PSO algorithm based on particle exploration for function optimization and the modeling of chaotic systems [J]. Soft Comput, 2015, 19: 3071-3081.
