单晶金属锆结构相变和熔化的分子动力学研究

薄锐,崔新林

(山西大学 理论物理研究所,山西 太原 030006)

0 引言

金属锆为第四族过渡金属,热中子吸收截面极低,热中子俘获截面小,耐热性、焊接及力学性能良好,抗辐射损伤能力强,耐酸碱腐蚀性好,目前被广泛应用于核反应堆的堆芯结构材料、铀燃料元件的包壳、聚合物的交联剂。由于有着较强的吸氢、氮、氧能力,锆还被用做反应堆中的慢化剂。还由于具备惊人的抗腐蚀性、极高的熔点、超高的硬度和强度,锆被用于航天材料和军工特种钢等[1-3]。锆最稳定的结构为六角密排hcp结构(α相),当加温到1 135 K时转变成体心立方bcc结构(β相)[4-6]。另外,在室温2.2 GPa下,hcp结构转变到特殊六角ω结构(ω相)[7-10]。锆及其合金在工业中各个领域的应用越来越广泛,对锆的材料性能的研究具有工程应用价值,人们已经进行了大量实验测量及理论计算来研究加载条件下金属锆的相变及力学性质。

1952年Bridgman首次发现锆在5.9 GPa下发生一级相变[11],随后Jamieson用X射线衍射实验证实了锆从hcp到ω结构的相变[12]。1970年McQueen等通过实验,首先发现了锆冲击绝热曲线上的间断,表明有固态相变发生[13]。Greeff通过锆的状态方程分析得到了锆的三种不同结构的自由能，从而计算得到ω相到β相的冲击相变为585 K,24 GPa[14]。Zong和Wenk等人通过X射线衍射实验得到了锆的hcp结构到ω结构的相变[15-16]。Yeddu等人采用3D弹性相场模型模拟静压下锆的hcp结构到ω结构的相变以及ω结构到hcp结构的相变[17]。郝彦军通过第一性原理方法计算锆的hcp结构到ω结构的相变和ω结构到bcc结构的相变,以及hcp结构和ω结构的弹性常数[6]。李纪锋采用分子动力学模拟方法对单晶锆的固态相变以及熔化特性进行了研究,主要研究的是锆的hcp结构到bcc结构的变化,计算自由能从而得到hcp到bcc的固态相变[3]。实验中主要采用X射线衍射或者实验后材料回收来研究锆的高压相变,理论方面主要以第一性原理研究低压相变,而针对锆的高温熔化和凝固研究较少,为此我们将利用lammps方法来研究锆的结构相变以及锆的高温熔化。LAMMPS即Large-scale Atomic/Molecular Massively Parallel Simulator,是美国Sandia国家实验室开发,是分子动力学模拟常用的一款软件,可以根据自己的需求修改lammps代码,lammps主要用于分子动力学模拟和计算,它可以在各种系综下模拟百万级的原子分子体系的固液气三态,并支持多种势函数。

1 初始结构的建立

使用Materials Studio软件建立单晶锆的三种结构,分别为六角密排结构hcp(α),体心立方结构bcc(β),特殊的六角结构(ω)[18],样品尺寸设置为30×30×30,如图1所示。

Fig.1 (a)Initial structure of single crystal zirconium(hcp(α)phase)；(b)Initial structure of single crystal zirconium(ω phase)；(c)Initial structure of single crystal zirconium(bcc(β)phase) 图1 (a)hcp(α)结构单晶锆的初始结构；(b)ω结构单晶锆的初始结构；(c)bcc(β)结构单晶锆的初始结构

体系所采用的是周期性边界条件,一是能保证模拟系统的粒子数恒定,二是能够消除边界效应。原子间采用的F-S势是在1984年Finnis and Sinclair首次提出的关于过渡金属的多项式的多体势模型。系统的总能为

式中右边第一项是对势,即原子间的相互作用能，第二项是多体相互作用吸引能。

搭建的单晶金属锆样品内部存在较大的内应力,样品结构不稳定,因此要对样品进行弛豫通过结构优化从而降低样品内部的应力,使样品内部应力降到最低,能量趋于稳定。对样品进行弛豫是通过能量最小化处理,具体采用共轭梯度法(CG),这是基于在最速下降法(SD)和牛顿-拉森法(NR)之间的一个方法,具有收敛性、稳定性高的特点。用共轭梯度法对初始样品进行能量最小化处理,最终使样品的结构趋于稳定,使其更加接近真实样品。表1列出了优化后得到的不同结构锆的晶格常数,初始体积和c/a比率,与其他计算结果和实验结果进行了对比。

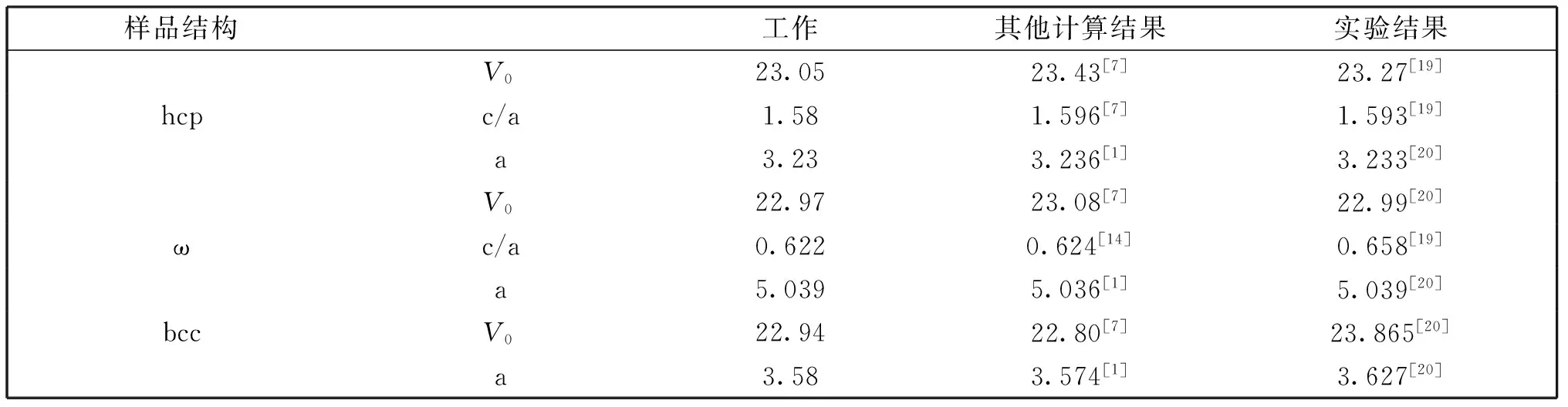
表1 不同结构样品的参数

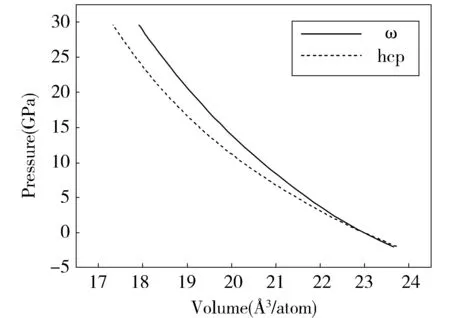
Fig.2 Curve of the volume of the structure with pressure of the hcp and ω structure of single crystal zirconium图2 锆的hcp结构和ω结构体积随压力变化的曲线

2 模拟结果

2.1 加压相变

在加压过程中有不同的加压方法,可以改变晶体的晶格常数来达到加压的效果,还可以采用另外一种方法Berendsen控压机制,本文采用Berendsen控压方法。利用lammps对样品进行加压,得到不同压力下的晶格常数,进而计算得到不同结构的P-V曲线,如图2所示。给出了锆的hcp和ω结构在加压过程中原子体积和所承受压力的关系曲线图,图中观测到锆的hcp结构和ω结构相交的压力点为0.2 GPa,说明hcp结构加压到0.2 GPa时结构发生变化,从hcp结构变成ω结构。Jona和Marcus等人采用全势线性缀加平面波方法通过计算吉布斯自由能和焓得到锆从hcp结构到ω结构的相变压力为8.7 GPa[10]。张和赵等人采用X射线衍射实验得到了在常温下锆从hcp结构到ω结构的相变压力为3.4 GPa[20-21]。郝彦军等人通过第一性原理得到在0K下锆从hcp结构转变到ω结构的压力点为0.7 GPa[6]。张等人通过第一性原理计算得到在0K下锆从hcp结构转变到ω结构的压力点为0.14 GPa[7]。本文通过分子动力学方法得到的结果与在第一性原理中的结果吻合,整体趋势符合锆的热力学性质。

Fig.3 (a) The microstructure of single crystal zirconium(hcp(α)phase) before the compression; (b) The microstructure of single crystal zirconium(ω phase)after the compression图3 (a)加压前hcp结构单晶锆的微观结构；(b)加压后ω结构单晶锆的微观结构

2.2 锆的加温

在分子动力学模拟中,一般是在系综下进行加温或者降温。在宏观条件约束下系综分为正则系综(NVT)、微正则系综(NVE)、巨正则系综(VTμ)、等温等压(NPT),等压等焓(NPH)。本文是在NPT系综下进行模拟,并且采用的是Nose-Hoover温控机制,这能使系统最大限度的接近热力学平衡态。在模拟过程中,首先对已经建好的锆的三种不同结构的单晶样品进行弛豫,采用共轭梯度法对样品进行能量最小化处理,使建立的样品模型趋于稳定,然后在NPT系综下进行加温,从零温开始加温到2 000 K,计算得到温度T、体积V、能量E等物理量的关系,并在不同的温度下观察并记录下原子的坐标,根据样品在加温以后原子坐标的变化从而进行分析。

2.2.1 锆的hcp到bcc结构相变

图4(a)为锆的hcp结构加温到1 500 K时,体积随温度的变化情况。由图4(a)可知,当温度从0 K上升到1 161 K时,体积发生了突变,说明hcp结构的单晶锆样品当温度升高到1 161 K时,结构发生了变化,追踪原子轨迹发现样品从hcp结构转变成了bcc结构,如图5所示。图4(b)为能量随温度的变化情况,单晶锆从0 K加温到1 161 K,能量随温度的增加而增加,符合金属的一般性质,当温度达到1 161 K时,能量发生突变,正是图4(a)得到的单晶锆从hcp结构到bcc结构的相变温度。图5(a)中hcp结构图为在加温之前的结构。图5(b)中bcc结构图为在大于1 161 K小于1 500 K内输出的原子坐标所得,而在小于1 161 K时没有bcc结构,由此得到在hcp结构加温到1 161 K时发生了相变,从hcp结构转变成了bcc结构。Greeff通过锆的状态方程得到了熵与温度的关系,体积和温度的关系，得到了锆从hcp结构相变到bcc结构的相变温度为1 135 K[14]。

Fig.4 (a)T-V curve of single crystal zirconium (hcp(α)phase)under high temperature;(b) T-E curve of single crystal zirconium(hcp(α)phase) under high temperature;(c) T-V curve of single crystal zirconium(bcc(β)phase) under high temperature;(d) T-E curve of single crystal zirconium(bcc(β)phase) under high temperature图4 (a)加温hcp结构锆得到T-V曲线;(b)加温hcp结构锆得到T-E曲线;(c)加温bcc结构锆得到T-V曲线;(d)加温bcc结构锆得到T-E曲线

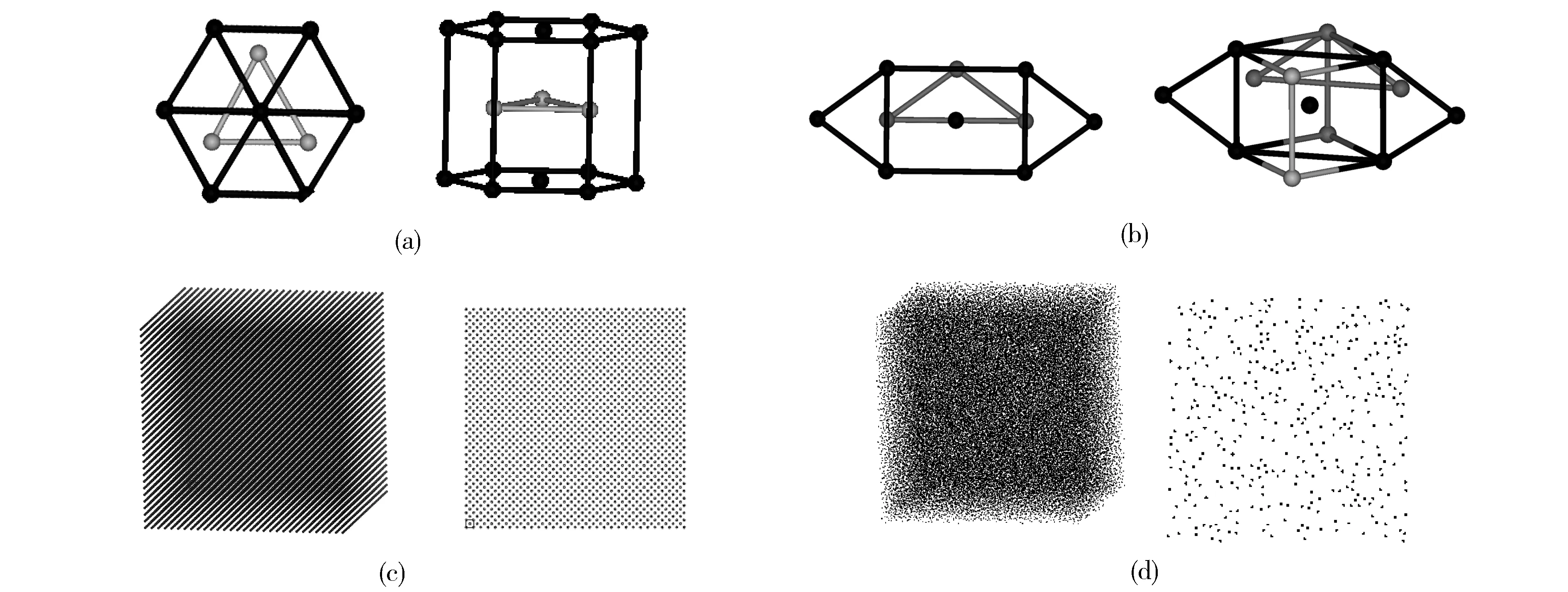
Fig.5 (a)Microstructure of single crystal zirconium(hcp(α)phase)before phase transition;(b)Microstructure of single crystal zirconium (bcc(β)phase)after phase transition;(c)Microstructure of single crystal zirconium(bcc(β)phase) before melting;(d)Microstructure of single crystal zirconium(bcc(β)phase)before melting图5 (a)相变前hcp单晶锆微观结构;(b)相变后bcc单晶锆微观结构(c)Bcc单晶锆熔化前结构;(d)Bcc单晶锆熔化后结构

2.2.2 bcc结构锆的熔化相变

Fig.6 Radial distribution functions under different temperatures图6 加温过程中锆的径向分布函数

对bcc结构的单晶金属锆样品加温发现当温度达到1 569 K时,体积有了一个大的变化,如图4(c)中所示,对样品中原子进行追踪,画出整体图像发现样晶体结构较为杂乱,如图5(d)所示,认为样品在此温度点开始出现熔化,进而得到熔化熔点在1 569 K,而在大气压强下的实验结果的熔点是2 128 K[22]。李纪锋通过回滞曲线法得到平衡熔点为2 010 K[3]。图4(d)中能量也在1 569 K发生了突变,与4(c)的结果吻合,说明bcc结构的单晶锆发生了熔化相变。观察体积突变前后样品图像,在样品体积突变前图像较为规整,如图5(c)所示,其为bcc结构,而体积突变后的图像则较为杂乱,如图5(d)所示,原子杂乱无序排列,认为在此处发生了熔化相变。

图6为锆的hcp结构、bcc结构以及加温熔化以后的径向分布函数g(r)曲线,图中黑实线是hcp结构径向分布函数g(r),它的第一峰值为3.26Å,第二峰值为4.636Å。图中黑横虚线是bcc结构径向分布函数g(r),它的第一峰值为3.116Å,第二峰值为3.572Å。图中黑点虚线是锆熔化的径向分布函数g(r),观察发现加温到1 600 K时得到的径向分布函数第一峰变得宽且矮,第二峰和第三峰没了,说明样品的结构发生了固液相变,金属锆样品熔化。

3 结论

本文采用lammps研究了单晶金属锆的相变结构,首先建立α,β,ω三种结构的单晶金属锆样品,其后对其进行加温加压处理。在0 K下当压力达到0.2 GPa时发现单晶锆会由hcp结构相变到ω结构,并通过对原子位置微观结构的分析得到了相变压力为0.2 GPa。在加温研究中发现,在零压下,单晶锆在1 161 K时发生了相变,并且得到了hcp结构到bcc结构的原子位置微观结构,所得结果与理论值一致。在继续加温的过程中发现在1 569 K时单晶锆开始熔化,通过对原子位置微观结构进行分析得到锆的hcp结构到bcc结构的相变温度为1 161 K,bcc结构的熔点为1 569 K,所得结果与实验结果一致。

[1] 王保田.重金属及其氧化物高压相变的第一性原理研究[D].太原：山西大学,2011.

[2] 肖大武.锆金属动态力学性能及其本构关系研究[D].合肥：中国科学技术大学,2008.

[3] 李纪锋.单晶锆固态相变与熔化特性的分子动力学模拟研究[D].北京：中国工程物理研究院,2014.

[4] Jayaraman A,Klement W,Kennedy G C,etal.Solid-Solid Transitions in Titanium and Zirconium at High Pressure[J].PhysicalReview,1963,131(2):644-649.DOI:10.1103/physRev.131.644.

[5] Xia H,Duclos S J,Ruoff A L,etal.New High-Pressure Phase Transition in Zirconium Metal[J].PhysicalReviewLetters,1990,64(2):204.DOI:10.1103/physRevLett.64.204.

[6] Hao Y J,Zhang L,Chen X R,etal.Ab Initio Calculations of the Thermodynamics and Phase Diagram of Zirconium[J].PhysicalReviewB,2008,78:134101.DOI:10.1103/physRevB.78.134101.

[7] Zhang S,Zhu Y,Zhang X,etal.First-principles Study on the Structural Stabilities,Electronic and Elastic Properties for Zirconium under Pressure[J].ComputationalMaterialsScience,2010:179-183.DOI:10.1016/j.commatsci.2010.07.023.

[8] Xia H,Ruoff A L,Vohra Y K.Temperature Dependence of theω-bcc Phase Transition in Zirconium Metal[J].PhysicalReviewB,1991,44:10374.DOI:10.1103/physRevB.44.10374.

[9] Schnell I,Albers R C.Zirconium Under Pressure:Phase Transitions and Thermodynamics[J].JPhys:CondensMatter,2006,18:1483-1496.DOI:10.1088/0953-8984/18/5/001.

[10] Jona F,Marcus P M.Zirconium Under Pressure:Structural Anomalies and Phase Transitions[J].JPhys:CondensMatter,2003,15:5009-5016.DOI:10.1088/0953-8984/15/29/312.

[11] Bridgman P W.The Resistance of 72 Elements,Alloys and Compounds to 100 000 Kg/cm2[J].ProcAmAcadArts&Sci,1952,81:165.DOI:10.2307/20023677.

[12] Jamieson John C.Crystal Structures of Titanium,Zirconium,and Hafnium at High Pressures[J].Science,1963,140:72.DOI:10.1126/science.140.3562.72.

[13] McQueen R G,Marsh S P,Taylor J W,etal.Chapter Ⅶ-The Equation of State of Solids from Shock Wave Studies[J].High-VelocityImpactPhenomena,1970:293-417.DOI:10.1016/B978-0-12-408950-1.50012-4.

[14] Greeff C W.Phase Changes and the Equation of State of Zr[J].ModellingSimulMaterSciEng,2005,13:1015-1027.DOI:10.1088/0965-0393/13/7/001.

[15] Zong H,Lookman T,Ding X,etal.The Kinetics of theωtoαPhase Transformation in Zr,Ti:Analysis of Data from Shock-recovered Samples and Atomistic Simulations[J].ActaMaterialia,2014,77:191-199.DOI:10.1016/j.actamat.2014.05.049.

[16] Wenk H R,Kaercher P,Kanitpanyacharoen W,etal.Orientation Relations During theα-ωPhase Transition of Zirconium:In Situ Texture Observations at High Pressure and Temperature[J].PhysicalReviewLetters,2013,111:195701.DOI: 10.1103/physRevLett.111.195701.

[17] Yeddu H K,Zong H,Lookman T.Alpha-omega and Omega-alpha Phase Transformations in Zirconium under Hydrostatic Pressure:A 3D Mesoscale Study[J].ActaMaterialia,2016,102:97-107.DOI:10.1016/j.actamat.2015.09.005.

[18] Kaufmann E N,McWhan D B.Electric Field Gradient at Ta in Group-IVB Metals[J].PhysicalReviewB,1973,8:1390.DOI:10.1103/physRevB.8.1390.

[19] Olinger B,Jamieson J C.Zirconium:Phases and Compressibility to 120 Kilobars[J].HighTempHighPress,1973,5:123.

[20] Zhao Y,Zhang J,Pantea C,etal.Thermal Equations of State of theα,βandωPhases of Zirconium[J].PhysicalReviewB,2005,71:184119.DOI: 10.1103/physRevB.71.184119.

[21] Zhang J,Zhao Y,Pantea C,etal.Experimental Constraints on the Phase Diagram of Elemental Zirconium[J].JournalofPhysicsandChemistryofSolids,2005,66:1213-1219.DOI:10.1016/j.jpcs.2005.03.004.

[22] Young D A.Phase Diagrams of the Elements[M].Berkeley,New York,Los Angeles,London:University of California Press,1991.