附加周期和神经网络补偿的实时钟差预报模型

黄观文，崔博斌，张 勤，付文举，李平力，蔺玉亭

(1. 长安大学地质工程与测绘学院，西安 710054；2. 北京卫星导航中心，北京 100094)

0 引 言

全球导航卫星系统(GNSS)实时导航定位中，卫星钟差产品精度会直接影响高精度导航定位授时(Position navigation and timing, PNT)服务能力[1-5]。目前的北斗卫星导航系统(BDS)实时钟差产品包括两类：一类是卫星播发的实时广播星历，其每小时更新发播一组卫星钟差系数，用户收到系数后进行二次多项式插值或拟合预报获得实时钟差值，但现阶段BDS广播星历的实时钟差精度较低，一般为3～10 ns，难以满足分米级以上定位需求；另一类是北斗超快速钟差预报产品，是基于24 h实测钟差序列进行实时预报得到，但其每隔6 h更新预报。国内外学者在钟差预报方面建立了多种钟差预报模型[1-17]。然而，由于星载原子钟时频特性复杂且极易受外界环境影响，卫星钟差通常表现出显著周期变化与随机特性，这使得已有的钟差预报模型在应用中仍存在局限性。文献[2]与文献[3]指出多项式预报钟差时其预报误差会随着预报时间增加而显著变大，GM(1,1)预报精度受模型指数系数影响较大，文献[6]指出Kalman滤波精度优劣取决于对原子钟运行特性和随机先验信息等的认知程度，文献[7]指出时间序列存在模式识别和定阶难题，文献[8]指出谱分析模型的周期函数要根据较长的钟差序列才能可靠确定，文献[9]指出小波神经网络拓扑结构确定比较困难，文献[10]指出径向基函数神经网络选取的样本长度以及样本之间间隔的确定只能依据经验确定。而在这些模型当中，多项式模型和GM(1,1)模型是最为常用且具有代表性的预报模型。文献[11]与文献[12]指出顾及到星载原子钟频偏、频漂等物理特性及预报稳定性和精度，卫星钟差超快速预报模型一般采用多项式加一个主周期项模型，其精度相比广播星历钟差值有一定提升，约为2～6 ns，但仍无法满足实时分米级导航定位需求。现阶段针对北斗钟差预报模型的研究多是基于卫星钟物理模型展开，而对于拟合残差中不显著的系统噪声误差未能有效顾及，因此本文提出构建一种多项式结合周期项与BP神经网络的北斗超快速钟差预报模型，并利用实测超快速钟差数据进行了算法测试验证。

1 基础预报模型

目前BDS二代星载原子钟均为Rb原子钟，Rb钟具有显著的钟漂特性，因此选用二次多项式模型作为BDS卫星钟差基础预报模型[1-3]，其拟合式如下：

y(t)=a0+a1(ti-t0)+a2(ti-t0)2+Δi

(1)

式中：y(t)为历元时刻ti的卫星钟差，a0，a1，a2分别为卫星原子钟t0时刻的钟差、钟速和钟漂，Δi为钟差预报模型残差。

2 周期项模型

卫星在轨运行中会受到轨道运行周期与太空环境及各种摄动力干扰，因此在轨道钟差同步解算的超快速卫星钟差预报中应充分考虑轨道周期及系统摄动力影响。现阶段不少学者已在卫星钟差预报中加入周期项改正，考虑到在轨卫星钟的显著周期项通常与卫星轨道运行周期基本一致[1-5,11-12]，本文对BDS三种类型卫星钟模型各添加两个主显著周期项[11-12]，其中GEO和IGSO主显著周期为24 h与12 h，MEO主显著周期为12 h与6 h，结合式(1)，附加显著周期项的拟合预报模型为：

y(t)=a0+a1(ti-t0)+a2(ti-t0)2+

(2)

式中：p为周期误差总数，k为所附加的周期项次序；Λk，fk，φk分别为钟差周期项的振幅、频率和相位，Δi为每颗卫星经过附加周期项的二次多项式拟合后的残差。由于残差中不仅包括白噪声，还受到其他误差及环境影响而包含不规律的有色噪声。常规预报模型很难拟合非线性无显著规律的有色噪声，因此需要考虑引入非线性拟合模型对残差进行进一步补偿。

3 BP神经网络

BP神经网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程，是一种单向传播的多层向前网络，具有三层或三层以上的网络结构，包括输入层、中间层(隐层)和输出层。相关研究表明，仅有一层的隐含层模型结构神经网络可以实现任意非线性映射[8-10]，本文设置为三层模式即输入层、隐含层与输出层。考虑到本文输出值仅为钟差，因此输出层神经元个数为1；而隐含层的神经元个数选取对于模型的训练精度与速率至关重要，考虑到训练速率与模型精度，本文选取的隐含层神经元数目为6[9-10]。鉴于BP神经网络在误差非线性拟合方面的优点，本文选用BP神经网络对北斗拟合残差进行进一步训练与拟合预报。

BP算法实质是求取误差函数e的最小值问题，通过逆向误差传递，获取真实值与拟合值之间最优映射函数关系，其误差函数定义为：

(3)

式中:m为模型总层数。

在反向传播算法应用于前馈多层网络，采用Sigmoid为激发面时，可用下列步骤对网络的权系数Wij进行递归求取。注意对于每层有n个神经元的时候，即有i=1,2,…,n;j=1,2,…,n。对于第k层的第i个神经元，则有n个权系数Wi1,Wi2,…,Win。另外取多一个Win+1，用于表示阀值θi。并且在输入样本X时，取X={X1,X2,…,Xn,1}。通过权值的确定后，整体算法的执行步骤如下：

1)对权系数Wij置初值，对各层权系数Wij置一个较小的非零随机数(本文选取为1)，但其中Wi,n+1=-θi。

2)输入一个样本X={X1,X2,…,Xn,1}，以及对应期望输出Y={Y1,Y2,…,Yn}。

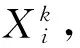
(4)

(5)

而对于其他各层，有：

(6)

式中:L为当前层神经元数目。

5)修正权系数Wij和阀值θ如下所示：

(7)

其中，

ΔWij(t)=Wij(t)-Wij(t-1)=

(8)

式中:θ为阈值,通过误差函数的最优值，获取权值与系数的最优解；η为学习速率，即步长，一般取0.1～0.4间的常数；α为权系数修正常数，取0.7～0.9间的常数[8-10]。BP神经网络预报算法流程为：通过式(3)～式(8)进行训练并获取最优的权值及拟合系数，进而利用获取的最优拟合系数结合二次多项式与周期项预报模型获取预报钟差序列。结合式(2)预报模型，附加BP神经网络的预报模型如下所示：

y(t)=a0+a1(ti-t0)+a2(ti-t0)2+

(9)

本文预报模型整体流程如图1所示。由图1可知，通过读入需要预报时间前两天实测钟差值，目前国际上实测钟差数据均选取一天的数据，本文分别选取了1至3 天的实测数据并建模预报，测试发现2 天效果更佳，3 天提升较2 天不明显且预报建模时间会增加，因此本文选取两天实测数据进行建模拟合。通过数据预处理剔除粗差与钟跳等异常值，获取二次多项式与周期项的拟合残差序列，将第1天拟合残差序列与第2天的拟合残差序列分别作为输入与期望输出值输入神经网络，通过BP神经网络训练获取最优拟合系数，从而利用第2天实测数据进行残差拟合预报并附加于二次多项式与周期项的预报模型上，进而达到对有色噪声的非线性最优拟合预报效果。

4 数据准备与精度评定

为了验证本文所提模型的可靠性和精度，分别选取了德国地学中心GFZ的超快速预报产品(GBU)与中国全球连续监测评估系统(iGMAS)产品综合的超快速预报产品(ISU)进行分析比较，时间为2017年年积日001-030天。BDS超快速钟差产品包含实测部分和预报部分。首先采用组合中位数粗差探测法对数据中存在的异常值进行探测与剔除。分别统计了在此时间段内GBU与ISU钟差预报精度，考虑到不同机构产品间存在基准差异，精度评定参考基准为其各自机构的事后精密钟差产品，并分别采用本文预报模型利用ISU与GBU实测钟差值进行预报，并与事后精密钟差进行精度评定。钟差精度δ采用标准差(Standard deviation,STD)作为卫星钟差精度指标[1-2]，具体如下所示：

(10)

(11)

5 预报精度分析

预报并统计了001-030天GBU及ISU钟差预报精度[18-19]，为了验证本文所提预报模型的正确性与精度，分别采用二次多项式(Quadratic polynomial, QP)，二次多项式结合周期项(Quadratic polynomial additional period, QP-Period)及本文所提附加神经网络的预报模型(Back propagation prediction, BP-PRE)与ISU和GBU预报产品精度对比分析，并分别展示了007 天三种不同预报模型及ISU与GBU超快速钟差预报残差结果(见图2～3)，其中使用GBU实测数据预报残差结果如图2所示。

从图2可以看出，本文预报模型的钟差预报精度相比GBU产品有显著提升。为了验证本文所提方法对于BDS卫星预报的普适性，同时给出利用ISU超快速实测钟差数据分别采用三种不同预报模型及ISU预报产品的007 天预报残差结果如图3所示。

从图2～3可以看出，GBU和ISU钟差预报精度与采用QP及QP-Period预报精度相近，而采用本文所提附加周期项与神经网络的预报模型钟差精度相比ISU及GBU有显著提升，6号卫星预报精度也有了较好改进，发散程度明显减小，24 h预报中残差也未出现显著增大。由图2～3的对比分析可知，采用本文附加周期项和神经网络补偿的北斗实时钟差预报模型，预报精度相比传统多项式预报模型有显著提升，相比现阶段公开提供BDS超快速预报服务的ISU与GBU产品精度也有大幅度改进。表明本文预报模型对于BDS卫星超快速预报有较好的效果。

为了从数值上比较不同预报模型精度，同时给出了001天-030天一周内不同模型分别在3 h,6 h,12 h和24 h预报精度平均值，统计数值结果如表1所示。

预报模型ISU/nsGBU/nsQPQP-PeriodISUBP-PREQPQP-PeriodGBUBP-PRE3h0.6030.5310.4590.3390.6200.6010.5610.5036h1.2211.0891.0450.8731.5171.4881.5451.33112h2.6972.7012.6492.3133.4923.4673.2793.01124h5.5335.4985.1794.6316.3516.2036.1355.251

从表1可以看出，ISU及GBU预报精度较低，因其预报模型仅为简单的QP或QP-Period。其中ISU产品预报精度略高于GBU产品，其原因为ISU为我国13家分析中心产品加权所得，相当于IGS综合多家分析中心产品，因此ISU对于异常数据有更好抗差性，钟差稳定性与精度相比GBU有进一步提升。本文预报模型精度相比QP与QP-Period模型精度均有较大提升。相比ISU产品，本文模型3 h,6 h,12 h和24 h预报精度分别提升了26.14%,16.46%,12.68%,10.58%；相比GBU产品，本文模型在3 h,6 h,12 h和24 h预报精度分别提升了10.34%,13.85%,8.17%和14.41%。以上对比结果也表明本文模型具有较高的钟差预报精度，且在24 h预报中残差发散现象明显变缓，预报残差序列更加稳定，精度提升显著。

6 结束语

常规北斗钟差预报模型拟合残差中仍存在非线性系统噪声影响，本文提出并构建了一种多项式结合周期项与BP神经网络的北斗超快速钟差预报模型，设计了算法实现流程。利用国内和国际两家机构北斗实测超快速钟差产品进行了算法测试验证。结果显示：利用本文模型得到的北斗超快速钟差产品，相比ISU精度提升约为10%～25%，相比GBU精度提升约为10%～15%。本文所构建的北斗钟差预报模型可用于提高目前我国北斗超快速钟差产品精度，同时，所提模型对于仅有MEO星座的GPS、Galileo和GLONASS也具有一定的普适性。

[1] 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究 [D]. 西安：长安大学, 2012. [Huang Guan-wen. Research on algorithms of precise clock offset and quality [D].Xi’an: Chang’an University, 2012.]

[2] Huang G W, Zhang Q, Xu G C. Real-time clock offset prediction with an improved model [J]. GPS Solutions, 2014, 18(1):95-104.

[3] Heo Y J, Cho J, Heo M B. Improving prediction accuracy of GPS satellite clocks with periodic variation behavior [J]. Measurement Science & Technology, 2010, 21(21): 073001.

[4] 黄观文, 余航, 郭海荣,等. 北斗在轨卫星钟中长期钟差特性分析[J]. 武汉大学学报(信息科学版), 2017, 42(7):982-988. [Huang Guan-wen, Yu Hang, Guo Hai-rong, et al. Analysis of the mid-long term characterization for BDS on-orbit satellite clocks [J]. Geomatics and Information Science of Wuhan University, 2017, 42(7): 982-988.]

[5] Huang G W, Zhang Q, Li H T, et al. Quality variation of GPS satellite clocks on-orbit using IGS clock products [J]. Advances in Space Research, 2013, 51(6): 978-987.

[6] 朱祥为, 肖华, 雍少为, 等. 卫星钟差预报的Kalman算法及其性能分析 [J]. 宇航学报, 2008, 29(3):966-968. [Zhu Xiang-wei, Xiao Hua, Yong Shao-wei, et al. Kalman for clock offset prediction and performance analysis [J]. Journal of Astronautics, 2008, 29(3): 966-968.]

[7] 周佩元, 杜兰, 路余,等. 多星定轨条件下北斗卫星钟差的周期性变化[J]. 测绘学报, 2015, 44(12):1299-1306. [Zhou Pei-yuan, Du Lan, Lu Yu, et a1. Periodic variations of beidou satellite clock offsets derived from multi-satellite orbit determination [J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1299-1306.]

[8] Xu B, Wang Y, Yang X. Navigation satellite clock error prediction based on functional network [J]. Neural Processing Letters, 2013, 38(2): 305-320.

[9] 王宇谱, 吕志平, 陈正生,等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013, 42(3):323-330. [Wang Yu-pu, Lv Zhi-ping, Chen Zheng-sheng, et al. Research the algorithm of wavelet neural network to predict satellite clock bias [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 323-330.]

[10] Wang Y, Lu Z, Qu Y, et al. Improving prediction performance of GPS satellite clock bias based on wavelet neural network [J]. GPS Solutions, 2017, 21(2): 523-534.

[11] 马卓希, 杨力, 贾小林. BDS星载原子钟周期项特性及预报研究[J]. 大地测量与地球动力学, 2017, 37(3):292-296. [Ma Zhuo-xi, Yang Li, Jia Xiao-lin. Research on prediction and characterization of periodic variations in BDS satellite clocks [J]. Journal of Geodesy & Geodynamics, 2017, 37(3): 292-296.]

[12] Wang B, Lou Y, Liu J, et al. Analysis of BDS satellite clocks in orbit [J]. GPS Solutions, 2015, 20(4): 1-12.

[13] Lv Y, Dai Z, Zhao Q, et al. Improved short-term clock prediction method for real-time positioning [J]. Sensors, 2017, 17(6):1308.

[14] 王颖, 徐波, 杨旭海. 一种利用泛函网络进行导航卫星钟差预报的方法研究[J]. 宇航学报, 2012, 33(10):1401-1406. [Wang Ying, Xu Bo, Yang Xu-hai. Research on the navigation satellite clock error prediction using functional network [J]. Journal of Astronautics, 2012, 33(10): 1401-1406.]

[15] 刘继业, 陈西宏, 刘强,等. 基于改进粒子群优化LS-SVM的卫星钟差预报研究[J]. 宇航学报, 2013, 34(11):1509-1515. [Liu Ji-ye, Chen Xi-hong, Liu Qiang, et al. LS-SVM based on improved pso for prediction of satellite clock error [J]. Journal of Astronautics, 2013, 34(11): 1509-1515.]

[16] 王宇谱, 吕志平, 王宁,等. 顾及卫星钟随机特性的抗差最小二乘配置钟差预报算法[J]. 测绘学报, 2016, 45(6):646-655.[Wang Yu-pu, Lv Zhi-ping, Wang Ning, et al. Prediction of navigation satellite clock bias considering clock’s stochastic variation behavior with robust least square collocation [J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 646-655.]

[17] 唐桂芬, 许雪晴, 曹纪东, 等. 基于通用钟差模型的北斗卫星钟预报精度分析[J]. 中国科学:物理学 力学 天文学, 2015(7):079502.[Tang Gui-Fen, Xu Xue-qing, Cao Ji-dong, et al. Precision analysis for compass satellite clock prediction based on a universal clock offset model [J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2015, 45(7): 079502.]

[18] 国际GNSS监测评估系统数据/产品[EB/OL].2017[2017].http://124.205.50.178/Product/TreePage/tree/nav_id/36/cate_id/37.html.

[19] 德国地学研究中心[EB/OL].2017[2017].ftp://ftp.gfz-potsdam.de/pub/GNSS/products/mgnss/.