偏度与峰度在脉冲激光回波分析中的应用研究
2018-03-09单聪淼孙华燕郑勇辉赵延仲
单聪淼,孙华燕,郑勇辉,赵延仲
(1.航天工程大学,北京 101416;2.卫星通信中心,北京 100094)
1 引 言
在脉冲激光探测中,回波脉冲的波形反映了目标的重要信息,根据目标回波信号的快速目标辨识是激光探测的最终目的。在脉冲回波波形的目标分类识别与特征提取研究方面,国内外学者做了大量研究[1-7]。Grardner C.S最早于1992年就提出了基于子波分解的目标辨识方法[8],利用最小均方误差理论对回波波形进行子波分解进而推断多个子目标的信息;Gustaav Tolt和Hakan Larsson对含有强漫反射背景干扰情况下的脉冲回波波形进行了解卷分析和基于此的窄脉冲提取[9],指出信号解卷积具有提高回波波形分解的能力;北京理工大学张辉等人提出了一种基于目标面元三维坐标和脉冲飞行时间的激光目标探测装置的回波脉冲功率描述方法[10],给出了目标回波波形的幅度-宽度联合识别方法。然而脉冲的能量与脉宽参数通常只能反映出目标的反射率与目标的深度信息,因此其他特征参量的建立对于回波脉冲分析来说是有一定价值和意义的。
基于以上背景,本文将用于描述随机变量分布特性的偏度和峰度参量引入到了回波波形的分析中来,用以表述回波波形的对称性和尖峭程度,并研究了目标散射特性与回波偏度和峰度的映射关系,为脉冲激光回波特征分析提供了重要依据。
2 原理分析
2.1 偏度和峰度对波形分析的引入
偏度和峰度的概念来自于对零均值随机变量分布特征的描述,两种参数分别描述随机变量概率密度函数的对称程度和尖峭程度,其定义分别如下:
r3x=E[x(n)3]=c3x(0,0)
(1)
r4x=E[x(n)4]-3(r2x)2=c4x(0,0,0)
(2)
为将其引入到对波形序列x(n)的分析,可以将x(n)序列的值等效为某随机变量的概率密度函数的值,坐标等效为该变量的随机取值,将x(n)波形序列做平移,使∑nx(n)=0,此时相当于对该随机变量做了零均值处理,然后求取该变量的偏度和峰度的计算式为:
(3)
(4)
如上两式即可表述为波形序列x(n)的偏度与峰度,相应地可得到归一化的偏度和峰度系数分别为:
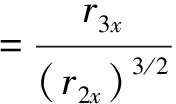
(5)

(6)
根据高阶统计量理论,服从高斯分布的随机变量的偏度与峰度均为零,这同样适用于对波形的分析,高斯波形的偏度与峰度是等于零的,波形的偏度反映了波形的对称性,峰度反映了波形的尖峭程度。两种参数可以作为波形特征的重要参量。
2.2 偏度和峰度分析在脉冲激光探测回波分析中的应用
根据高斯光束的传输理论和几何光学理论,如图1所示的激光辐照条件下,目标散射的回波波形可认为是受辐射区域内各散射点回波的叠加,设出光脉冲在时间和空间上均服从高斯分布,回波波形可表示为:

(7)
式中,λ为与大气衰减、有效接受面积等相关的回波衰减系数;P0为出光脉冲中心点的峰值功率;τ为与出光脉宽有关的常数;r(ω)表示散射体表面散射点至激光源处的距离随方向角变化的分布函数;γ(ω)是表面反射率随方向角变化的分布函数。
上式可以简化等效为出光脉冲波形与一个同目标形状和反射率相关的调制函数相卷积的形式:
W(t)=λ·[S(t)*f(t)]
(8)
式中,S为出光光束中心处的脉冲波形;f为目标调制函数,根据式(7),f可表示为:
由表5说明,土样1土壤中添加2%骨炭(A)化学修复剂时土壤中的重金属锌、铅、铬、铜、砷、镉含量均有所下降,其中在种有马铃薯的土壤区域主要污染物锌含量下降幅度最大,下降值为90.1mg/L。在种有油菜和马铃薯的土壤区域主要污染物砷含量下降幅度最大,最大值为1.0mg/L。
(9)
由上式可以看出,对于图1所示激光辐照条件,当目标表面的反射率和起伏随激光辐照方向变化较小时,f(t)是近高斯的,根据高斯波形卷积的性质,此时回波波形仍是高斯的。
反之,当目标表面反射率或起伏随激光辐照方向发生突变时,f(t)便偏离高斯波形,回波波形也随之偏离高斯波形。此时,利用前面偏度和峰度对回波波形分析,可以对回波形变做出判断,进而推断目标信息。
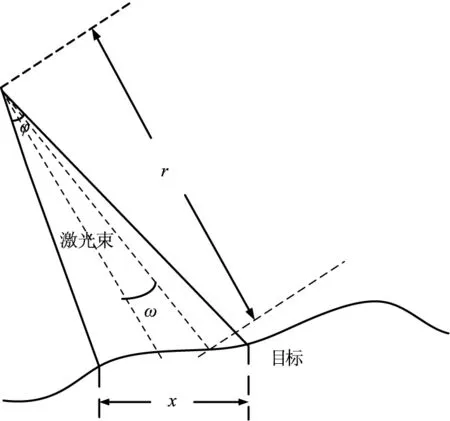
图1 激光辐照示意图
3 数值仿真及分析
针对前面的分析,用式(5)、(6)表述的波形偏度和峰度参量对回波波形做仿真处理与分析,分别对目标表面反射率和起伏在辐照方向上存在较弱变化和突变两种情况下的回波偏度与峰度做了对比实验,具体如下。
3.1 反射率和起伏变化较弱时的回波偏度峰度仿真实验
用随机白噪声对目标表面反射率和起伏的随机变化做表征,将其与高斯波形相叠加以对目标调制函数做近似,如图2(a)、(c)、(e)所示,他们依次为随机噪声由弱到强逐渐变化的的三种波形,将其分别与出光脉冲波形做卷积得到回波波形,见图2(b)、(d)、(f),对三种不同程度随机起伏下的回波波形的偏度与峰度做多次统计计算,得到了两参数的统计分布情况如表1所示。

图2 反射率和起伏变化较弱时的目标调制函数及其回波
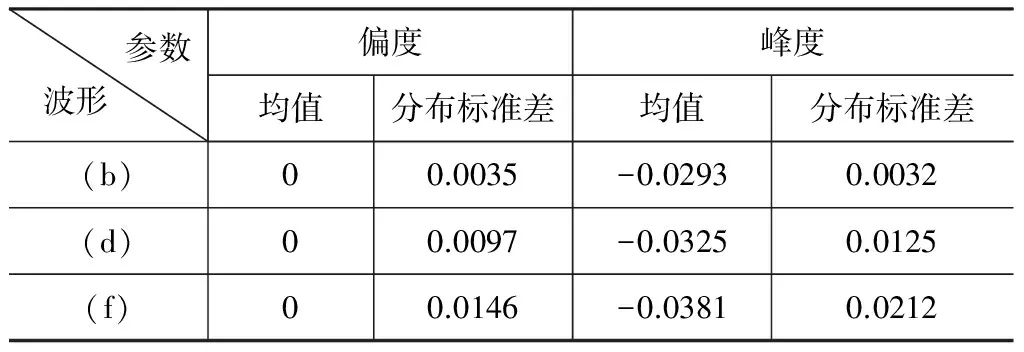
参数波形 偏度峰度均值分布标准差均值分布标准差(b)00.0035-0.02930.0032(d)00.0097-0.03250.0125(f)00.0146-0.03810.0212
由图2和表1可以看出,当目标面的反射率和起伏变化较弱时,回波仍为较好的高斯波形,偏度接近于零,峰度为一个较小的幅值,且随着起伏强度的增加,回波的偏度和峰度参数变化越强。
3.2反射率和起伏存在突变时的回波偏度峰度仿真实验




图3 反射率和起伏存在突变时的目标调制函数及其回波
由以上结果可以看出,目标面的反射率或起伏突变会致使回波波形偏度或峰度出现明显变化,对于有强散射点存在的情况,散射点偏离目标调制函数峰值较远时,回波的偏度和峰度均会呈现出较大的值;偏离峰值较近时,回波呈现出较大的偏度;恰好位于峰值时,则回波会呈现出较大的峰度。当目标起伏导致目标调制函数非对称时,回波也会呈现出较大的偏度。

表2 反射率和起伏存在突变时的回波偏度与峰度
由表2还可以看出,不同调制函数下的回波偏度与峰度的值也是不同的,因此,偏度和峰度两个参量能够有效地表征出这些突变,从而为脉冲激光探测的回波波形分析提供重要的依据。
4 结 论
本文将用于描述随机变量分布特性的偏度与峰度引入到了波形分析中来,用以表征波形的对称性和尖峭程度,并通过理论分析和数值仿真,研究了两种参数在脉冲激光回波波形分析中的应用,当目标端的反射率或起伏出现突变时,回波的偏度与峰度能够对此有效地表征。
在实际应用中,目标的反射率和起伏分布异常复杂,回波受噪声的影响有时也不可忽略,因此在复杂目标场景和强噪声干扰下的回波波形分析也会更加复杂。另外,偏度和峰度仅仅为波形分析提供一种对称度和高斯度评价的参量,当出射激光脉冲不为标准高斯波形时,其应用尚有待进一步研究。
[1] HUANG Tao,Hu Yihua.Information processing of lidar for obscure target[J].Electro-optic Technology Application,2011,26(1):27-30.(in Chinese)
黄涛,胡以华.遮蔽目标的激光雷达回波信息处理[J].光电技术应用,2011,26(1):27-30.
[2] ZHAO Nanxiang,HU Yihua.Relation of laser remote imaging signal and object detail identities[J].,Infrared and Laser Engineering,2006,35(2):226-229.(in Chinese)
赵楠翔,胡以华.激光遥感成像信号与目标细特性关系研究[J].红外与激光工程,2006,35(2):226-229.
[3] GU Yu,HU Yihua,HAO Shiqi,et al.Study on influence of filter back-projection on laser reflective tomography[J].Laser & Infrared,2015,45(12):1500-1505.(in Chinese)
谷雨,胡以华,郝士琦,等.激光反射层析成像中滤波反投影算法特性研究[J].激光与红外,2015,45(12):1500-1504.
[4] HU Xuejuan,LIU Chengxiang,YANG Jinghui,et al.Convolution approach for zebra stripe feature extraction of infrared paper currency image[J].Laser & Infrared,2012,42(10):1196-1201.(in Chinese)
胡学娟,刘承香,杨锦辉,等.基于卷积运算的纸币红外图像斑马线特征提取[J].激光与红外,2012,42(10):1196-1201.
[5] ZHANG Shuai,LIU Zhiguo,ZHAO Qian,et al.Research on the jamming mechanism of high repetition laser on laser seeker[J].Laser & Infrared,2015,45(12):1467-1472.(in Chinese)
张帅,刘志国,赵乾,等.高重频激光对激光导引头的干扰机理研究[J].激光与红外2015,45(12):1467-1472.
[6] WANG Yupeng,ZHAO Liangbo,YU Kaiguo,et al.Study and simulation of semiconductor laser ranging based on msequence[J].Laser & Infrared,2016,46(2):159-164.(in Chinese)
王誉鹏,赵梁博,余开国,等.基于m序列的半导体激光测距技术研究与仿真[J].激光与红外,2016,46(2):159-164.
[7] DONG Jing,CHEN Rui,LI Xiaolong,et al.Lidar coherent detection and feature ettraction of moving target based on micro-doppler effect[J].Chinese Journal of Lasers,2012,39(10):1014001-1-4.(in Chinese)
董晶,陈蕊,李小龙,等.运动目标微多普勒效应的激光雷达相干探测及特征提取[J].中国激光,2012,39(10):1014001-1-4.
[8] Grardner C S.Ranging performance of satellite laser altimeters[J].IEEE Transaction on Geoscience and Remotesensing,1992,30(5):1061-1072.
[9] Gustaav Tolt,Hakan Larsson.Waveform analysis of lidar data for targets in cluttered environments[J].Proc.of SPIE,6739:A01-A09.
[10] ZHANG Hui,WANG Yongtian.Scattering characteristics and targets recognition of laser TDD[J].Acta Photonica Sinica,2005,34(1):32-34.(in Chinese)
张辉,王涌天.激光目标探测装置的回波特性及目标识别技术研究[J].光子学报,2005,34(1):32-34.
