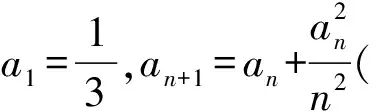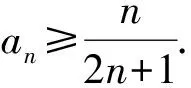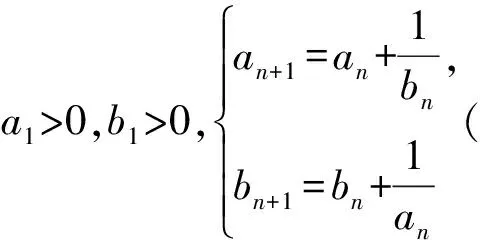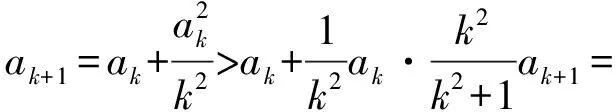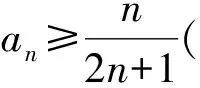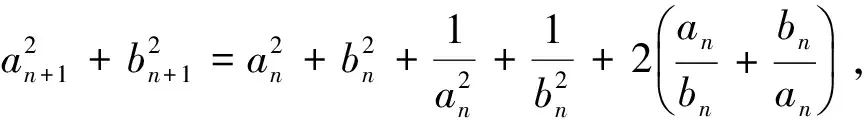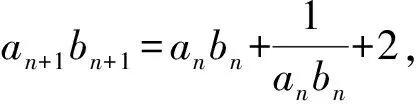数列与数学归纳法
2018-03-09
●
(杭州市基础教育研究室,浙江 杭州 310003)
数列与数学归纳法
●王红权
(杭州市基础教育研究室,浙江 杭州 310003)
数列是历年数学高考重点考查的内容之一,浙江省的数列试题既重视基础又强调关联,客观题立意概念的本质,综合性试题对学生的素养要求很高,不仅要有较强的估算和运算能力,还要求有敏锐的判断力.文章举例分析近几年浙江省数学高考对数列的考查,列举所考查的内容、常用方法和命题方向等.
复习备考;数列;数学归纳法;不等式
1 知识内容
数列和数学归纳法内容涵盖:数列的概念和表示法;等差和等比数列的概念、通项公式和求和公式、与一次函数和指数函数的关系、简单应用;可以利用错位相减法求和的数列;数学归纳法等.
2 命题分析
2012—2017年数列试题题量、总分值和知识点的分布如表1所示.
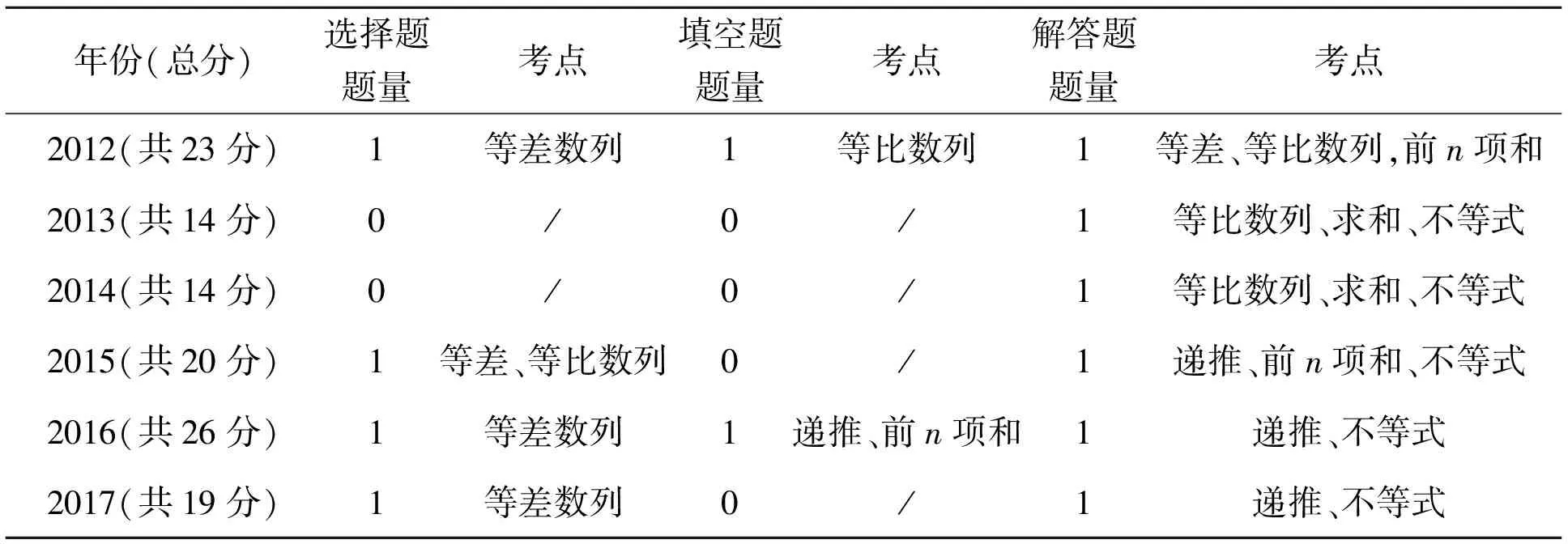
表1 2012—2017年数列试题题量、总分值和知识点的分布情况
从表1观察,数列试题考查内容较为稳定,涉及等差和等比数列的定义、通项公式和求和公式,可化为等差或等比数列的数列求和、数列的递推公式以及不等式相关的综合性问题等.但从总分值分布的角度看,随年份的波动较大;从题型分布看,也具有较大的不确定性.
从题目功能看,选择题一般考查对概念的理解,要求考生判断出正确的选项,不需要做过多的运算;填空题则要求在理解概念的基础上,选择适当的算法并正确求解;解答题则强调综合,但2012—2014年和2015—2017年的试题存在显著的差异,前者命题的立意以数列基本性质的综合为主,后者则以递推公式为基础,主要考查的是不等式的性质,综合性和难度显著提高.
3 典题剖析
考点1等差和等比数列的基本问题.
以等差和等比数列的概念、通项公式和求和公式为基础,利用基本量法求解,是高考考查数列内容的方向之一.这类问题要求考生熟悉定义,合理选择,计算准确.
例如:复习等差数列的通项公式、求和公式,理解等差数列基本问题的求解策略:“知三求二”.例1以表格的形式给出问题,可以更直观地感知基本量是求解等差数列问题的基本方法.等比数列类似.
例1[1]已知数列{an}是等差数列,根据表2中已有的信息完成其他信息.
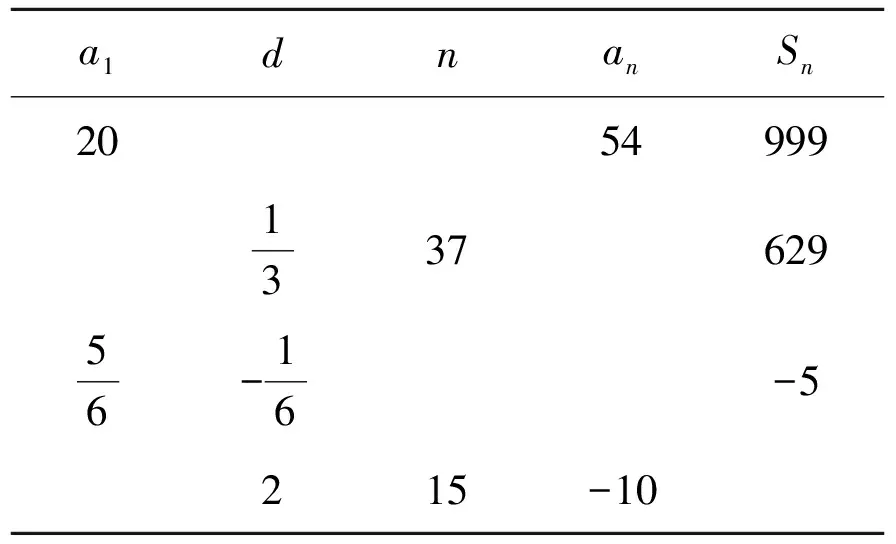
表2 等差数列{an}的相关信息
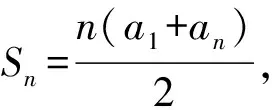
( )
A.60 B.62 C.63 D.66
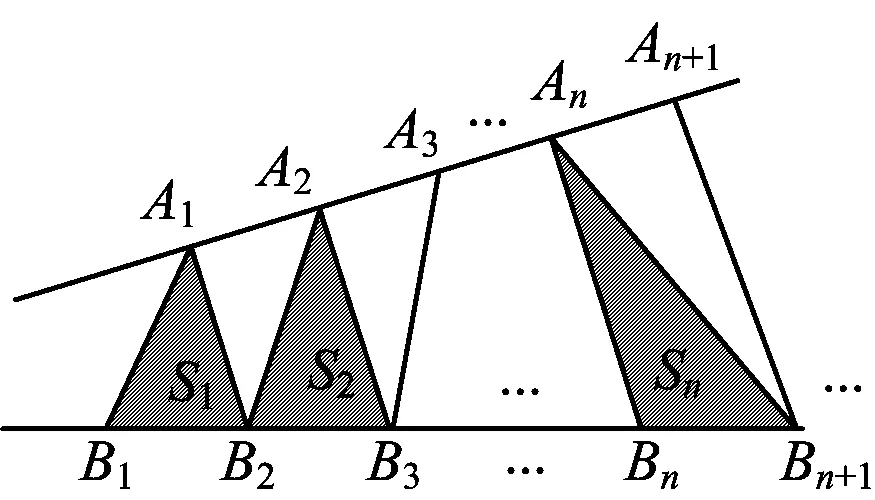
图1
(2014年浙江省高中数学学考试题第22题)
2)如图1,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,其中n∈N*;|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,其中n∈N*,P≠Q表示点P与点Q不重合.若dn=|AnBn|,Sn为△AnBnBn+1的面积,则
( )
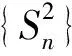
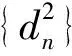
(2016年浙江省数学高考理科试题第8题)
3)已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4+S6>2S5”的
( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
(2017年浙江省数学高考试题第6题)
分析这类问题可以选择利用定义和基本量计算进行解决,但性价比不高.
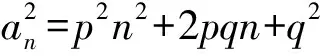
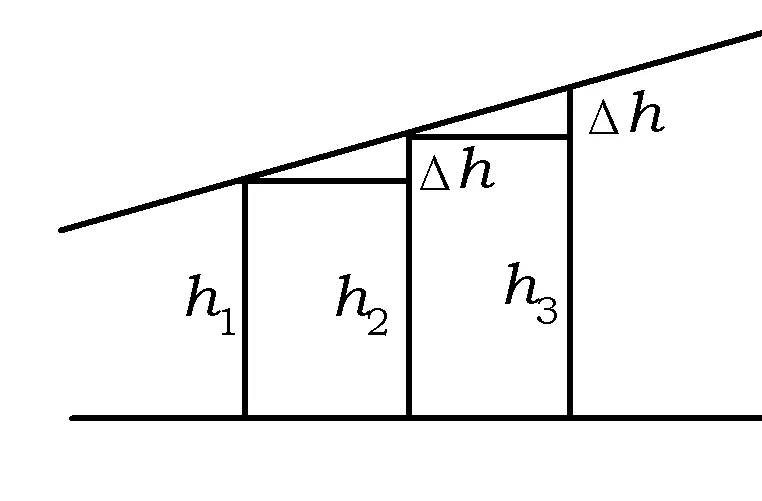
图2
2)由三角形的面积想到高线,由于所有的三角形都等底,因此只需要考查图2中的高线hn组成的数列{hn},根据图2,显然{hn}是等差数列,这便是等差数列的几何模型,直观而且本质.
3)思路1已知条件可变形为
S4-S5>S5-S6,
即
a5 从而d>0,反之亦然.故选C. 思路2已知条件可变形为 学习数列当从数入手,利用代数手段精准刻画其变化规律,利用其函数背景揭示数列的本质,特别是等差数列还可以辅之以几何直观帮助理解,揭示知识间的内在联系[2].第1)小题和第2)小题较好地考查了等差数列通项公式的线性特征,其中第1)小题从函数的角度给出了刻画,第2)小题用几何直观加以刻画,深刻而本质;第3)小题用函数对等差数列的前n项和公式给出了函数刻画,揭示其非线性特征.只要深刻理解其本质,并不依赖计算,这也是浙江卷选择题的最大特点. 考点2可化为等差和等比数列的问题. 由递推公式得出数列变化规律是解决数列问题的常见方法之一,若题干中出现了一般数列的递推公式,则可以考虑转化为等差或等比数列的递推公式.常见的有两类:一类是低阶线性递推关系;另一类是以分式形式出现的递推关系,通过适当的变形,可化为线性递推或直接转化为等比数列. 例31)已知数列{an},{bn}满足:a1=-1,b1=2,an+1=-bn,bn+1=2an-3bn(其中n∈N*),则b2 015+b2 016=______. bi+2+bi+1=-2(bi+1+bi), 从而数列{bi+1+bi}是以b1+b2=-6为首项、-2为公比的等比数列,于是 b2 015+b2 016=-6×(-2)2 015=3×22 016. 2)由已知得到 从而 即 类似地,有 即 两边取对数,得 因此 即 故取jn=2n-1即可. 注适当的变形是解决这类问题的关键,往什么方向变形,心中要有基本的模型,如线性递推an+1=an+p可以构造等比数列,分式形式两边取倒数可以构造等差或等比数列,指数形式an+1=panq(其中p>0,an>0)两边取对数可以构造等比数列. 考点3数列与不等式相关的问题. 数列是特殊的函数,函数的很多性质需要用不等式加以刻画,数列和不等式结合的相关问题在近3年浙江省数学高考命题中均作为压轴题出现,考查的重心由数列常用性质转移到递推公式的复杂变形和不等式的证明. (2016年浙江省杭州市第二次质量检测数学试题第18题) (2015年浙江省数学高考理科试题第20题) 所以数列{an}单调递增,从而an≥a1=1,于是 即 事实上, (1) 即 (a1-a2)+…+(an-an+1)= 同第1)小题分析可知 所以 累加得 从而 an-an+1≥anan+1, 即 累加得 即 由第①小题得an≤2an+1, 从而 即 累加得 于是 即 注1第1)小题和第2)小题虽然都是构建“差结构”,但两个问题之间还是有区别的:第1)小题是通过恒等变形建构“差结构”;第2)小题既可以通过恒等变形建构,也可以通过放缩获得中间结构,然后化为“差结构”,其实这样的放缩更接近浙江省数学高考试卷中的数列不等式证明的本质,如2008年和2017年的浙江省数学高考压轴题是完全一样的思路.当然第2)小题也可以用数学归纳法证明,请读者自己完成. 注2没有“差结构”就没有“前n项和”,换言之,在递推公式立意的试题中,有“和”就需要关注“差结构”. 1.若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个数列有 ( ) A.13项 B.12项 C.11项 D.10项 2.某种细菌在培养过程中,每20分钟分裂一次(一次分裂为两个),经过3个小时,这种细菌由一个可以繁殖成 ( ) A.511个 B.512个 C.513个 D.1 024个 3.设{an}是等差数列,Sn为其前n项的和.若正整数i,j,k,l满足i+j=k+l(其中i≤k≤l≤j),则 ( ) A.aial≤ajakB.aial≥ajak C.SiSl≤SjSkD.SiSl≥SjSk 4.已知等差数列{an},等比数列{bn}的公比为q(其中n,q∈N*),设{an},{bn}的前n项和分别为Sn,Tn.若T2n+1=Sqn,则an=______. 5.已知数列{xn},满足(n+1)xn+1=xn+n,且x1=2,则x2 018=______. 1)证明:an 参考答案 1.A 2.D 3.A 6.证明1)易知an>0,从而 于是 进而 因此,当n≥2时, 故 an<1. an<1(其中n∈N*), 于是 an 2)当n=1时,显然成立.由an<1,知 从而 即 因此,当n≥2时, 即 故 4+4×49=200. 200+200=400, 因此 a50+b50>20. [1] 邬建云,王红权.“等差数列”习题课的教学实践[J].中国数学教育,2015(12):25-30. [2] 王红权,王凯.聚焦新特点 研究新策略——2017年浙江省数学新高考复习备考研究[J].教学月刊,2017(5):47-52. 收文日期:2017-10-30; 2017-12-02 王红权(1970-),男,浙江杭州人,中学高级教师.研究方向:数学教育. O122.4 A 1003-6407(2018)03-0037-05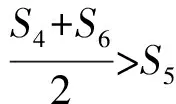
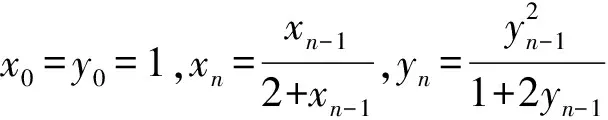
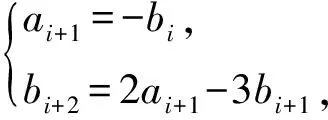
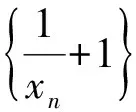
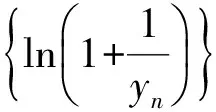


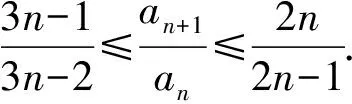
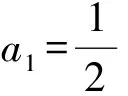
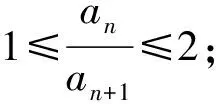
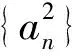
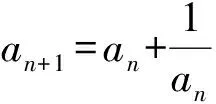
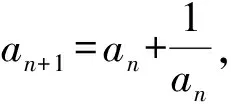
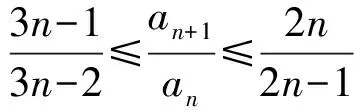
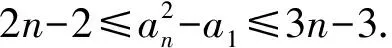

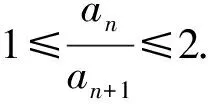

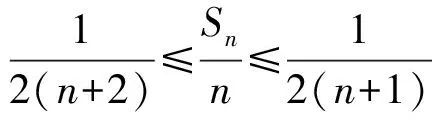
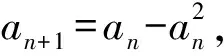
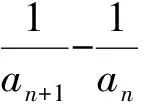
4 精题集萃