重基础 重本质 重联系
——高三复习课“当函数遇上绝对值”课堂实录与感悟
2018-03-09
●
(湖州市教育科学研究中心,浙江 湖州 313000)
●凌 红
(湖州中学,浙江 湖州 313000)
重基础重本质重联系
——高三复习课“当函数遇上绝对值”课堂实录与感悟
●王勇强
(湖州市教育科学研究中心,浙江 湖州 313000)
●凌红
(湖州中学,浙江 湖州 313000)
文章通过对2017年浙江省高中数学课堂教学评比活动中的一节评比课,给出课堂简要实录和一些观课感悟.在观课过程中感受到整堂课教学目标精要、教学设计精美、教学语言精练,并通过反思感悟到高三复习教学课堂中要重基础、重本质、重联系,以期对高三数学复习教学有所帮助.
课堂教学评比;课堂实录;重基础;重本质;重联系
历时3天的2017年浙江省高中数学课堂教学评比活动在浙江省诸暨市落下帷幕,此次评比活动主题新、内容新、形式新.本次评比的主题为“基于数学问题本质的揭示与数学思想方法理解及应用的复习教学设计和实践”,前所未有.赛课内容改变了传统开设概念课、章节起始课等的做法,首次选择开设复习课,是以2014—2017年学考、高考中的典型题目为例开设一节高二或高三的复习课.赛课课题提前两天公布,对各地市选送的参赛选手的备课及教学展示提出了非常高的要求,更真实地体现了选手的数学功底和教学水平.
本次评比活动立意新,反响强烈,吸引了500多位数学教师的积极参与,让每位参与者都感到受益匪浅.在这次评比活动中,来自湖州中学的凌红老师开设的“函数复习课”得到了专家评委和观课教师的一致好评,被评为一等奖第一名.下面给出这节评比课的课堂教学简录和观课后的感悟.
1 课堂教学过程简单实录
师:函数是高中数学的重要内容之一,在近几年的学考和高考中,含绝对值的问题是热点.那么当函数遇上绝对值时,会演绎出怎样精彩的故事呢?
1.1 复习旧知,强化概念
师:绝对值是什么?
生(众):一个数的绝对值必大于等于0.
师:绝对值有什么几何意义?
生(众):数轴上的距离.
师:今天,我们以距离为视角,来研究形如f(x)=|[ ]-( )|的函数的最值问题.
评注通过“绝对值是什么”“绝对值有什么几何意义”这两个简单的问题,让学生回忆起“绝对值”这个概念的基本内涵,从而确立本节课的复习主题.
1.2 自主探究,把握本质
例1函数f(x)=|x-1|,其中x∈[-1,1]的最大值为______.
评注通过最简单的问题,唤醒学生对于绝对值几何意义的认识,为变形做好铺垫.
变形1设函数f(x)=|x-b|,其中x∈[-1,1],b∈R.记f(x)的最大值为g(b),则当b变化时,g(b)的最小值为______.
师:|x-b|的几何意义是什么?
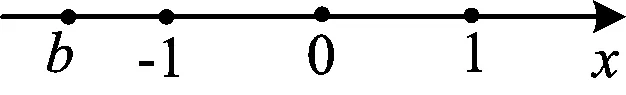
图1
生(众):数轴上表示
x
,
b
的两点间的距离(如图1).
师:当b变化时,f(x)的最大值随之变化,则f(x)为b的函数,即为g(b).那么,请同学们观察,当b为多少时,g(b)可以达到最小,此时g(b)的最小值是多少?
生(众):当b=0时,g(b)的最小值为1.
师:如果在平面直角坐标系中画出函数y=x,其中x∈[-1,1]和y=b的图像,怎样体现出距离?
生1:在函数y=x,其中x∈[-1,1]的图像上任取一点,作x轴的垂线,与y=b的交点与该点之间的竖直距离.
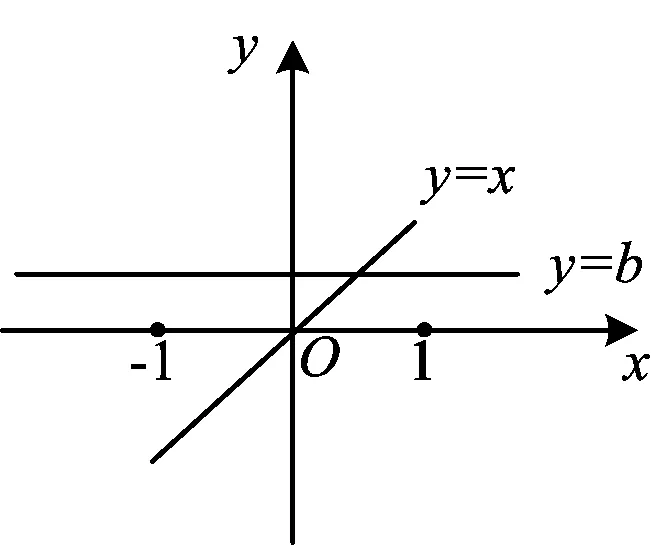
图2
师:这位同学回答得非常准确.也就是说可以将一条竖直直线水平移动,看它与两个函数交点之间的距离即可.如果y=b的图像如图2所示,f(x)的最大值在哪里取到?
生(众):在x=-1处.
师:当b变化时,函数y=b的图像上下移动,当b为何值时,最大值g(b)可以达到最小?
生(众):b=0.
师:如果直线y=b上移,那么在x=-1处,g(b)>1;当y=b下移时,在x=1处,g(b)>1,故g(b)的最小值为1.
师:对于变形1,用绝对值的本质——距离,解决了含参函数最大值的最小值问题.我们并没有求出函数最大值的具体表达式,而是直接得到了它的最小值,两步并做一步走,真可谓事半功倍!
评注从常数到参数的变化,从数轴上的距离引向两个函数之间每一个x处的竖直距离,体现了数形结合的思想.
变形2设函数f(x)=|x2-2x-b|,其中x∈[-1,1],b∈R.记f(x)的最大值为g(b),则当b变化时,g(b)的最小值为______.
师:请同学们思考一下,同桌之间可以交流,从距离的角度来看该怎么求解?
生2:先画出y=x2-2x的图像,可知该函数在[-1,1]上单调递减,且值域为[-1,3],因此当b=1时,g(b)的最小值为2.
师:这位同学在平面直角坐标系中,研究了两个函数y=x2-2x,其中x∈[-1,1]和y=b在每一个x处的竖直距离,直接得到答案.有没有同学在数轴上解决这个问题?
生3:令t=x2-2x∈[-1,3],就是变形1了.
师:这位同学利用换元法,将x2-2x看成整体,就化归为变形1了.至此,我们已经解决了任意一个函数与水平直线的“距离”问题了.
评注从一个自变量到一个代数式,体现了整体思想和转化化归的思想.
例2设函数f(x)=|x2-ax-b|,其中x∈[-1,1],a,b∈R.记f(x)的最大值为M(a,b),则M(a,b)的最小值为______.
师:这个函数研究的是什么之间的距离?
生(众):y=x2与y=ax+b之间的距离.

图3
师:在图3中如何看距离呢?
生(众):平移竖直直线,考虑与两个函数图像交点之间的距离.
师:距离的最大值与什么参数有关?
生(众):与a,b都有关系.
师:我们把函数的最大值记为M(a,b),接下来是不是找一条直线,使得最大值M(a,b)达到最小就行了?请同学们找找看,到底哪条直线符合要求.
教师请两位学生到黑板上画出自己认为符合要求的直线.
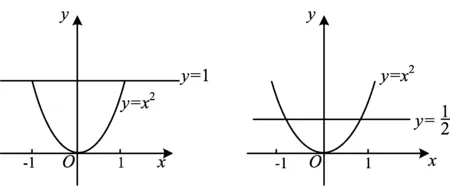
图4 图5
师:我们来分析一下,最大值的最小值分别为多少?


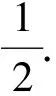
学生们纷纷表示没有找到.但是发现反例总是出现在f(-1),f(0),f(1)处.
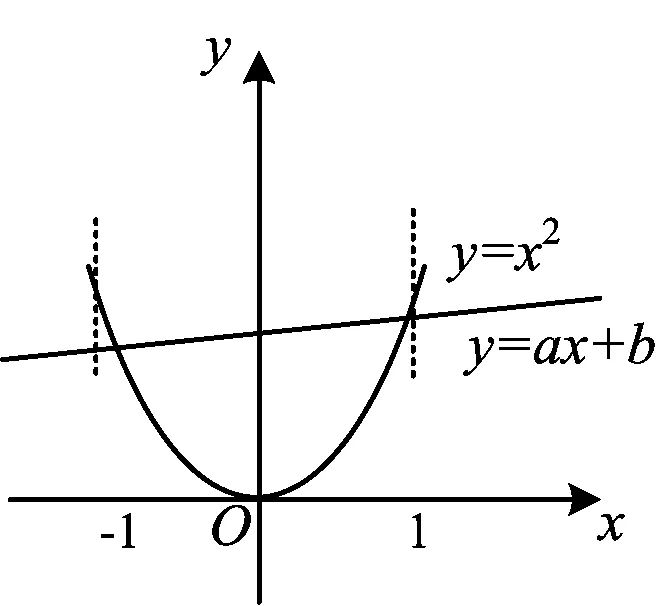
图6


评注从水平移动直线到任意转动直线的变化,揭示问题的本质不变.
变形3设函数f(x)=|x2-ax-b|,其中x∈[0,1],a,b∈R.记f(x)的最大值为M(a,b),则M(a,b)的最小值为________.
师:如果定义域为[0,1],那么答案又是多少呢?
师:有没有不同意见?
生5要求上黑板画线,如图7所示.
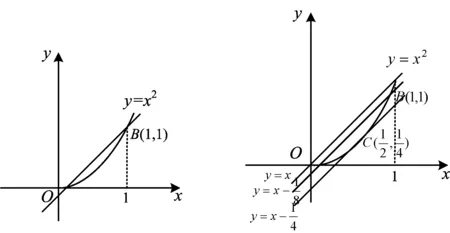
图7 图8
师:这条直线是如何确定的?比如说斜率是多少?
生6:把它平移使得直线与抛物线相切.
师:这条切线是如何确定的?是随便找一个点作为切点画出的?
生7:与直线OB平行.
师:这时,我们就知道所画直线的斜率为1了.
评注从两端点连线呈水平状态到倾斜状态的变化,隐含了一般具有凹凸性函数与任意动直线纵向距离最大值何时最小的作法.
1.3 学以致用,感悟思想

1)当a=0,b=1时,写出函数f(x)的单调区间;

3)若对任意实数a,b,总存在实数x0∈[0,4],使得不等式f(x0)≥m成立,求实数m的取值范围.
(2015年1月浙江省数学学考试题第34题)
师:请同学们运用今天学习的“以距离为视角”的方法来解决这个含绝对值的函数学考题.
1.4 课堂小结,提炼本质
这节复习课我们初识“当函数遇上绝对值”,学习了用“绝对值的本质——距离”来分析问题和解决问题.
数学问题的形式是千变万化的,但是数学概念的本质是不变的.教师在复习教学时,应该回归概念的本质,做到以不变应万变,揭示数学问题的本质,从而形成前后逻辑连贯的数学思想方法,为解决千变万化的数学问题提供帮助.
评注教师在每个环节结束时都及时地与学生一起进行小结反思,在整堂复习课的最后再次小结,对整节课的核心——绝对值的距离本质作出梳理和提炼.
2 观课感悟
2.1 观课感受,三“精”高效
1)教学目标精要.
这堂课中像例2、例3的解决方法有许多,包括利用绝对值的定义、采用分类讨论的思想方法、利用绝对值的几何意义采用数形结合的思想方法(即绝对值的距离本质来破题)、采用绝对值三角不等式和最值的定义来解答等.但笔者认为数学教学是“慢”艺术,一节课只有40分钟,如果把所有好的数学方法、好的数学思想都打包发给学生,往往会出现因空间不足而无法解压的现象.因此,教学目标的设计要符合学生的实际,并提前预测其达成度;课堂容量是教学目标的抓手,教学容量是为目标服务的,必须紧密地贴合.
整堂课凌老师的教学目标就是构建一个模型——纵向距离,来解决一个问题——绝对值函数问题.教学目标看似简单,但对学生而言却是一个全新的视角,如果40分钟能够掌握,那么将是体现“学为中心”的成功的教学实践.这堂课实践下来,凌老师做到了教学目标精要.
2)教学设计精美.
整堂课的教学设计精美,思路清晰,环节自然,过程流畅,层次分明,体现了凌老师深厚的教学功底.在教学情景创建上,从绝对值的定义出发,看似简单,却妙不可言,一则拉近了与学生的距离,降低复习课起始的入门门槛;二则揭示了“形如f(x)=|[ ]-( )|的函数的最值问题”的数学本质,为后续由浅到深、逻辑连贯、层次分明的阶梯型教学的顺利进行奠定了基础.在教学素材的选择上,从最简单的f(x)=|x-1|,其中x∈[-1,1]入手,围绕绝对值的几何意义,从一维到二维,引导学生从“水平距离”到自然构建“纵向距离”,再通过变式层层推进,强化对模型的理解与应用,凸显了数学问题的本质,非常切合本次评比活动的主题.
美中不足的是课堂上没有明确说出“纵向距离”,没有给出类似“纵向距离”这种说法,学生的体会和感悟相对会浅一些.正所谓:名不正则言不顺.
在教学策略上,并没有刻意去追求课堂氛围的热闹,而是更多的关注对学生思维的启迪,对数学思想方法的渗透.在教师的引导下,学生的思维始终处在活跃状态,少的是表面的喧闹,多的是思维的发散,所有探究出的结论都来自学生,但教师对每一个问题解决后的点评却又能再次提升学生的数学思维,整节课40分钟都让学生在绿色、生态的环境中自然地学习数学、享受数学,进而提高学生的数学核心素养.
3)教学语言精练.
整堂课凌老师教学语言精练,娓娓道来,教态优雅大方,极具亲和力,很容易起到“亲其师,信其道”的效果.板书规范科学,精炼准确;教学语言严谨,丝丝入扣;所画图形清晰工整,激发思维;课件大方清爽,突出重点.众所周知,教学语言的规范科学是对教师的最基本要求,精炼准确和生动形象是提高课堂效率的有力保障,而激发思维可以充分体现数学教学的主要目的.凌老师的教学语言虽然激情不足,但也独具特色,在40分钟的课堂教学中对教学信息的传递、对课堂纪律的管理、对学习动机的激发、对学生数学思维的促进都起着“润物细无声”的作用,使得整堂课的教学目标在不知不觉中就已经达成了.
2.2 观课感悟,复习课要三“重”同行
高三复习课要重基础.特别是第一轮复习,复习教学的重心要放低一些.俗话说:基础不牢,地动山摇.因此,在高三复习时,不能想当然地认为所讲知识是以前学过的教学内容,就对基础知识的复习走马观花,强调死记硬背或匆忙地一笔带过,急于去解题甚至是去分析难度较大的高考题,以为这样才能吸引学生、才能培养学生的思维能力.可贵的是,在本次评比活动中出现了不少重基础的课例,起到了很好的观摩示范的效果.
像前面的课例中,凌老师上课初始通过“什么是绝对值”“绝对值有什么几何意义”这两个基础的问题来复习绝对值概念,以学生为本,帮助学生打好基础,另外在后面发展思维能力的教学过程中,也是从难度较低的数学问题出发,由浅到深逐步变式,从一维到二维,从横向距离类比到纵向距离,根据学生的最近发展区,始终强调对绝对值、距离等基本概念和转化化归、数形结合等数学基本思想的理解和掌握.
高三复习课要重本质.这里的本质指的是概念的本质和思想方法的本质.高三教师要在凸显概念本质和提炼思想方法本质的教学上狠下功夫,精选例习题,向经典致敬,在解题的过程中不断回归数学概念和定义.《普通高中数学课程标准(实验)》中指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.数学课程要讲逻辑推理,更要讲道理,通过典型例子的分析和学生自主探索活动,使学生理解数学概念、结论逐步形成的过程,体会蕴涵在其中的思想方法,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态.”以上课例中引导学生通过典型问题及3个变式的分析和自主探索,使学生理解绝对值概念的本质和内涵,逐步体会蕴涵在其中的“以距离为视角”的数学思想方法,契合了《普通高中数学课程标准(实验)》中阐述的重本质的课程性质.
高三复习课要重联系.复习教学中通过主线分明的问题串将数学概念和数学思想方法联系起来,从而提高学生对数学问题整体的认识.教学过程中应该注重沟通课堂前后各部分内容(包括课后作业)之间的联系,通过对经典数学问题进行多个维度的变式探究等方式,使学生体会数学问题之间的有机联系,感受数学的整体性,进一步理解数学问题的本质,提高学生分析问题、解决问题的能力.
若教师能在高三复习教学中引导学生重基础、重本质、重联系,使学生养成良好的思考问题的习惯,以“不变”作为思考问题的出发点,凸显数学问题本质的通性通法来应对“万变”的数学题目,才能摆脱题海,事半功倍,使复习课真正能够做到轻负高效.
收文日期:2017-11-03;
2017-12-04
王勇强(1974-),男,浙江金华人,中学高级教师.研究方向:数学教育.
O123.1
A
1003-6407(2018)03-0016-04
