隧道中橡胶气囊阻漏受力分析模型及试验验证

闫澍旺，陈 静，岳长喜，孙立强，郎瑞卿

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

近年来，随着地下空间不断地开发利用，在修建地铁及隧道过程中，经常遇到易发生渗漏或者涌水突泥的地下环境，如古河道和渗透性较大的土层．这种土层可能存在于隧道经过的某一区域，由于勘察时钻孔间距较大，未能发现不利土层，故而未采取有效的防范措施，施工时就可能发生大量地下水渗漏涌入隧道的事故[1]．芝加哥、天津和上海等城市都发生过涌水进入地下隧道的情况[2-5]．大量的地下水不断涌入隧道，不仅会损害机械设备、影响正常施工，还会造成地表地下水位的降低，对周围建筑物的沉降产生不利影响，致使其开裂甚至倾斜．为减少工程损失，避免涌水面积扩大，需要尽快将涌水区隔离．当隧道发生大量漏水时，一般来不及使用堵漏剂等材料进行密封，目前工程中常用现浇混凝土坝体将水阻隔在一侧，再利用灌浆等方法进行止水．这种方法耗材多、建造及拆除费力费时，且不能及时解决问题．因此，亟需快速高效的临时性装置进行阻水，以确保生命财产安全以及工程的顺利实施．本文提出采用橡胶气囊作为隧道抢险挡水的临时性结构，如图 1所示，隧道中气囊直径 5.5,m，长度 11,m．这种方法是将气囊充气使其快速膨胀后与隧道壁贴紧，利用气囊与隧道壁之间的摩阻力来抵抗渗漏体的压力，将涌水渗漏阻隔在气囊一端(简称“阻漏”)，以保护机械设备和施工环境，并为进一步处置争取了时间．这种方法可以快速应对险情，在几小时之内便可完成橡胶气囊的充灌，及时达到阻漏效果，高效便捷且省工省时．

图1 在隧道中阻漏的橡胶气囊Fig.1 Photos of plugging rubber airbag

目前，国内外对气囊在隧道中阻漏的应用研究较少，Martinez等[6]针对隧道中突发洪水的情况，提出将一个或数个气囊安装在隧道顶部，当险情发生触动开关机制，气囊可迅速膨胀从而起到阻隔作用．Sosa等[7]进行了干、湿两种状态下气囊材料与混凝土面的摩擦系数试验，并进行小比尺模型试验，气囊在摩阻力不足情况下会产生滑移．Sosa等[8]进行了大比尺试验，将气囊安装在货运隧道人行道的上方，由于隧道形状存在较深的锐角，气囊与隧道壁不能完全贴紧，故在堵水过程中，凹凸角处有一定的漏水量，可用泵将积水抽走．我国对气囊的研究主要限于对小直径的气囊在管道中堵水堵气的应用，例如江庆海[9]、王惠英[10]根据在工程现场采用气囊封堵小直径管道的技术，证明可以取得预期的效果．靳亚兵等[11]通过多次试验，找到适于堵漏的强度高、弹性好、抗冲耐磨的气囊，提出在气囊外表增加一个固定尼龙网兜，可以增加气囊的强度．张国森等[12]介绍了气囊管内封堵法的工艺机理、设备需求、施工工序及安全措施．李明[13]提出同等内压下，气囊材料拉力与其直径成正比关系，所以直径越大对气囊材料的抗拉强度要求越高，通过气囊堵水试验说明当水压小于气囊内压时堵水有很好的效果且方便快捷．张建等[14]对半球形气枕式充气膜结构在不同外荷载作用下的受力状态进行分析，说明采用理想气体状态方程可以模拟气枕在外部荷载作用下内压的变化情况．余龙等[15]提出承压气囊的力学特性和极限承载力的计算方法，并通过算例验证方法的可行性，为船用气囊下水的安全使用提供了指导．

以上研究均未涉及气囊在隧道中受到侧压后的变形和受力，这是决定气囊能否正常工作的关键问题．因为气囊属于膜结构，其抵挡外压的大小不仅由摩阻力决定，也取决于其形状变化的特点，并且因气囊四周受隧道管壁正向力约束，其变形和失效模式也不同于常规的膜结构．尤其对于隧道中的大直径气囊，由内压产生的材料拉力和需要阻挡的侧向力远远大于普通小直径气囊，其滑移失效后的危害也更加严重，因此研究气囊在外压作用下变形、滑移的控制条件十分必要和关键，是气囊在隧道中使用的先决条件.

本文将建立弹性气囊的受力分析模型，考虑材料的拉伸特性，结合气囊在隧道中的边界条件和受力条件，对气囊一端在外压作用下的变形特性进行研究，从而得到气囊自开始变形至极限状态的过程中的变形规律和内压增长的计算公式，确定气囊保持稳定时所能够抵挡的最大外压．同时，得到气囊得以有效工作的 3个控制条件，即外压不能大于内压、外力不能大于最大静摩阻力和材料张力不能大于抗拉强度．采用伸缩性较大、变形明显的橡胶材料进行模型试验对气囊变形特性和阻漏控制条件进行验证，为气囊在实际工程中的应用提供设计依据．

1 气囊阻漏的受力分析和控制条件

1.1 基本假定

为研究气囊置于隧道中的形状变化、受力特性以及稳定工作的控制条件，做出如下假定．

(1) 隧道横截面为圆形，气囊与隧道壁完全贴合；

(2) 气囊为均质弹性材料，张力与变形关系符合胡可定律；

(3) 气囊一端的外压为均匀荷载；

(4) 气囊受压时，气囊内温度恒定，内部气体满足气体状态方程

式中：p0为气囊未受荷时的内部压强，kPa；Va为内部压强为p0时气囊的体积，m3；p1为气囊受荷之后的内部压强，kPa；Vb为内部压强为p1时气囊的体积，m3.

为分析气囊受外压后的变形过程，分别建立二维、三维模型进行研究．由于二维模型概念比三维模型更加简明扼要，计算更为便捷且结果一般偏于安全，故先研究二维模型情况下气囊的形状和受力特点，为三维模型的建立奠定基础．

1.2 二维模型研究

1.2.1 气囊一端受压后的变形过程

在隧道中，气囊受隧道壁的环向约束，径向可以在内压作用下自由变形．当左端有均匀荷载时，气囊变形过程如图 2所示，其中图 2(a)为气囊未受外压时的初始剖面形状；图 2(b)为左端受荷过程中的形状；图 2(c)为气囊在外压作用下变形至极限状态时的形状．超过极限状态后，气囊将不能保持稳定，由于滑动而阻漏失效．下面针对气囊的受力和形状变化展开研究，从而确定每个阶段气囊的准确形状和各部分的受力特性．

1.2.2 气囊初始形状及受力分析

设定隧道直径为D，气囊的初始充气压力为p0．受隧道的约束，气囊由紧贴管壁的直线段l0和两端的曲线段组成．曲线段上任意一点的受力分析如图3所示[16]．其中，θ为变形后气囊Ⅰ区圆弧段的圆心角；R为变形后气囊Ⅰ区圆弧段的半径，m；ll为变形后气囊Ⅰ区每侧增加的直线长度，m．由受力平衡关系可知

式中：T为气囊曲线段上任意一点的拉力；r(x)为纵坐标为x位置处的曲率半径；p(x)为纵坐标为x位置处的压强．

气囊内空气的质量忽略不计，故内部各点压力p(x)＝p0为定值，曲线段各点在内压和拉力作用下平衡且内压垂直于切线方向，故各点的拉力T相等，根据式(2)可得r(x)为定值，曲线段为圆弧，又因曲线段与直线段相切，故可确定曲线段为半圆形．因此气囊初始形状可以确定，由Ⅰ区、Ⅲ区两个半圆和Ⅱ区一个矩形组成，剖面图如图2(a)所示．

图2 气囊在侧压力下的变形过程Fig.2 Deformation of rubber airbag under lateral pressure

图3 气囊曲线段上一点的受力分析Fig.3 Force analysis of one point on the curve segment of rubber air-bag

取Ⅰ区中半圆为研究对象，气囊上任意一点的轴向拉力如式(3)所示，即气囊在初始状态时，各点的径向拉力都相等．由于隧道壁的约束作用，不考虑气囊的环向拉力．

1.2.3 气囊一端受压后的形状及受力分析

当气囊一端受到外荷载作用时，气囊在外荷载、内部气压力、管壁支撑力和摩阻力的共同作用下发生变形，气囊体积由Va变化到Vb，内部压强由p0变化到p1，通过对气囊变形后的受力及变形协调分析，可确定气囊的内压和形状，尤其是变形至极限状态时的内压和形状，它是确定气囊能够抵挡多大外压和是否发生滑动的关键问题．

1) 气囊受荷端的形状及受力分析

气囊受荷端Ⅰ区，曲线段外部的压力迅速增大，导致内外压差减小，其上任一点受力如式(4)所示，各点内外压差相等，而曲线段上拉力也处处相等，可得曲线段为一段圆弧，长度为ly＝Rθ，其中R为圆弧半径，θ为圆心角．由于曲线段处于卸荷状态，拉力减小，气囊为弹性材料，故Ⅰ区总长度收缩，受荷前的半圆除构成此时的圆弧ly，多出的长度变为贴壁的两条直线段长度为ll，因此变形后的气囊剖面如图2(b)所示．

式中：pw为外部压强，kPa；T1l为变形后气囊Ⅰ区圆弧的拉力，kN/m．

由式(4)可知，如果外部压强pw大于气囊内部压强p1，而气囊材料只能承受拉力不能承受压力，Ⅰ区圆弧段将内凹，此时没有外力可以平衡内凹曲线的张拉力，气囊形状不能保持，将会滑动失效．因此气囊作为膜结构，且在此约束条件下，正常工作时的外部压强不能大于气囊的内部压强，此处内部压强是指变形后的内压p1，如式(5)所示．

随着外压增大，圆弧曲率半径逐渐增大，直线段长度ll逐渐增大，当外压pw等于内压p1时，Ⅰ区气囊圆弧部分内外压差为零，气囊拉力也为零，剖面形状趋近于一条直线，如图 2(c)所示，这是气囊Ⅰ区变形的极限状态，也是气囊能保持稳定的极限状态．此时气囊Ⅰ区的极限形状确定如下：原Ⅰ区的半圆形变形收缩后可分为 3部分：长度为D的一段直线和长度为llult的两段贴壁直线．Ⅰ区收缩前长度为 πD/2，拉力为T0，受力后其中长度l′,收缩至长度D，对应的拉力为T1l＝0，根据气囊拉力变化的胡克定律，确定l′,的长度计算见式(6)～式(7)，进而可得到长度llult(见式(8))，此长度是拉力为T0状态下的长度．

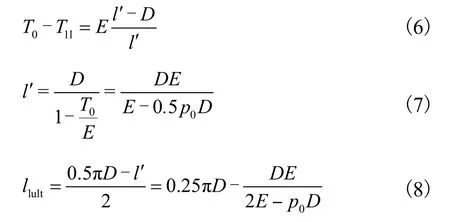
式中：l¢为对应于变形后长度为D的变形前的长度，m；llult为极限状态时Ⅰ区每侧增加的直线段长度，m.

2) 气囊自由端的形状及受力分析

在外压作用下，气囊受荷端有收缩趋势，故其整体体积减小且内压增大．自由端在内压作用下材料拉力增大，气囊伸长，Ⅲ区的半圆形拉伸为两个直线段lr和一个新的半圆形，如图 2(b)所示．极限状态时Ⅲ区每侧增加的直线长度lrult如图2(c)所示．计算过程见式(9)～式(12)．

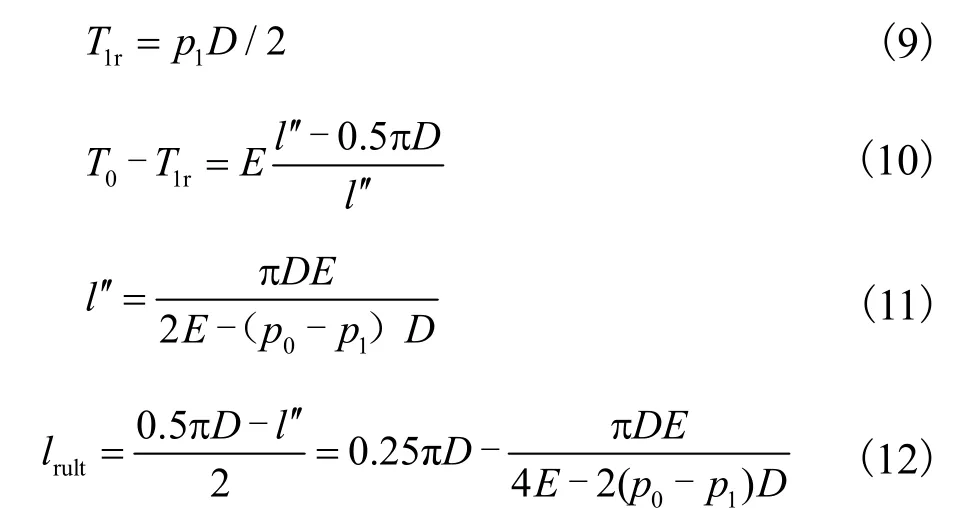
式中：T1r为气囊Ⅲ区变形后圆弧的拉力，kN/m；l¢为对应于变形后长度为 0.5,πD的变形前的长度，m；lrult为极限状态时Ⅲ区每侧增加的直线段长度，m．

通过以上对气囊受荷端和自由端的分析可知，在受外压作用后，受荷端处于卸荷状态，而自由端处于张拉状态，自由端的张拉力在极限状态时达到最大，需使材料的抗拉强度满足张拉力的需要(见式(13))，否则气囊在受荷过程中会因强度不足而发生材料破坏．

式中Ts为气囊材料的抗拉强度，kN/m．

3) 气囊直线段受力分析

气囊Ⅱ区在极限状态下的直线段长度lt由原始直线长度、受荷端和自由端在变形后增加的直线段长度共同组成(见式(14))，如图 2(c)所示，但此时的长度lt对应的张力为T0，需根据气囊实际的受力状态，确定气囊最终极限状态的直线段长度lz．极限状态下直线段的受力分析如图4所示，左端受到拉力为T1l，右端受力为T1r，并受摩阻力fs以及内压p1和隧道壁支撑力pn的作用，lt计算过程见式(14)～式(16)．

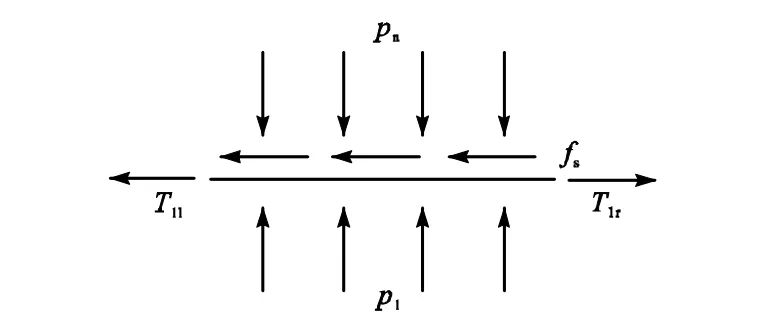
图4 气囊在极限状态时直线段的受力分析Fig.4 Force analysis of the line segment of rubber airbag in limit state

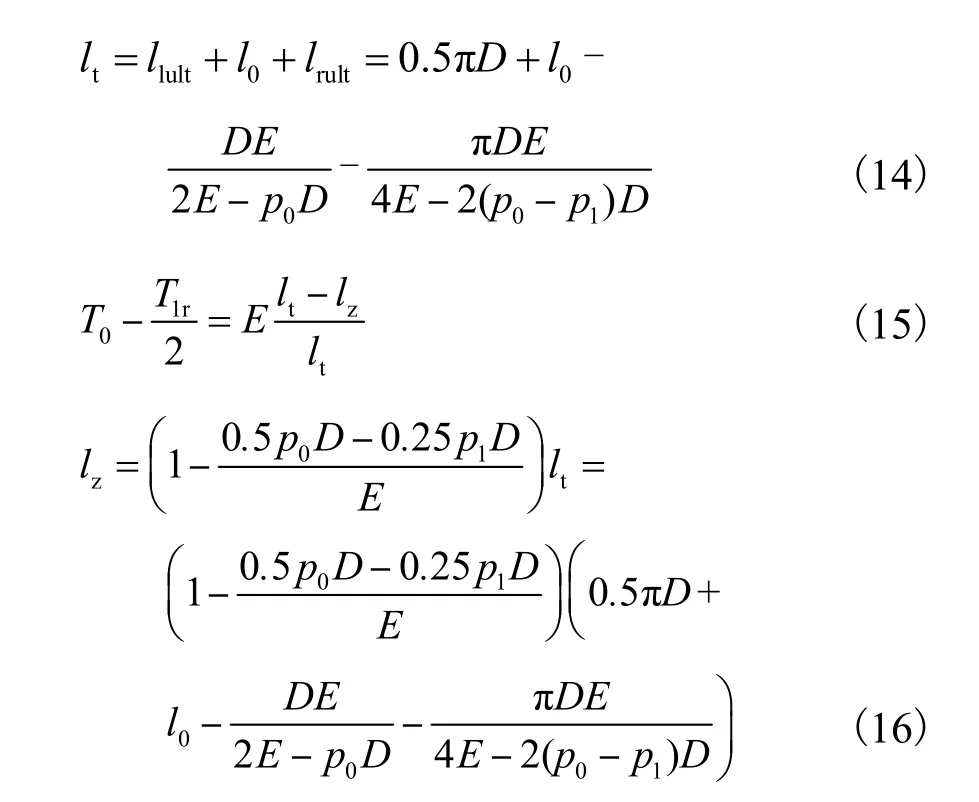
1.2.4 气囊极限状态时的内压

根据对受荷端、自由端以及直线段部分的分析，可确定气囊在极限状态的形状和受力．根据气体状态方程式(1)，与式(17)、(18)联立可求得极限状态气囊内压p1，也是气囊可承受外压的最大值，以此作为气囊设计的依据之一．

式中：V1、V1¢为初始状态、极限状态Ⅰ区的体积，m3；V2、V2¢为变初始状态、极限状态Ⅱ区的体积，m3；V3、¢为初始状态、极限状态Ⅲ区的体积，m3；Va、Vb为初始状态、极限状态的总体积，m3．

1.2.5 气囊整体受力分析

以上气囊的变形和受力分析是基于气囊与管壁不产生相对滑动为前提的，故需使气囊与管壁的最大静摩阻力大于外部荷载(见式(19))．极限状态下气囊在隧道中的水平向受力分析如图 5所示(其中fsult为气囊极限状态时最大静摩阻，kPa)，可以得到气囊能够抵挡的最大荷载pwult．

式中：Fsult为气囊极限状态时的最大静摩阻力，kN；pwult为气囊极限状态时能抵挡的最大外荷载，kPa．

图5 气囊极限状态时水平向受力分析Fig.5 Horizontal force analysis of rubber airbag in limit state

1.3 三维模型研究

1.3.1 气囊一端受压后的变形过程

三维气囊变形的过程与二维情况相同，见图6．

图6 气囊在侧压力下的变形过程Fig.6 Deformation of rubber airbag under lateral pressure

1.3.2 气囊初始形状及受力分析

将二维的推导分析思路应用于三维情况，气囊的初始充气压力为p0，左右两端(Ⅰ区、Ⅲ区)为半球形，中间部分(Ⅱ区)为圆柱体，如图6(a)所示．

以Ⅰ区半球为研究对象，根据气囊内压在水平方向上投影的合力等于气囊材料拉力，得到气囊的轴向拉力为

对比式(3)可知，根据三维模型分析，气囊拉力是二维模型所得拉力的 1/2，所以依据二维模型计算结果来选择气囊材料偏于安全．

1.3.3 气囊受压后的形状及受力分析

1) 气囊受荷端的形状及受力分析

气囊左端受均匀荷载pw，Ⅰ区气囊内外压差减小，处于卸荷状态，半球形的气囊收缩为球缺和圆柱体的组合，球缺的半径为R，圆心角为θ，收缩成的圆柱体高度为ll，即为直线段增加的长度，如图 6(b)所示．

当外压pw等于内压p1时，Ⅰ区气囊圆弧部分内外压差为 0，气囊拉力为 0，趋近于一个平面，收缩后圆柱体的高度为llult，如图 6(c)所示．Ⅰ区的半球形收缩后由圆形隧道平面S和高为llult的圆柱体侧表面组成，圆形隧道平面S是由原来半球形中的面积S¢收缩而成，半球形剩下的面积构成圆柱体的侧表面．根据胡克定律，长度llult计算过程见式(22)～式(27)．

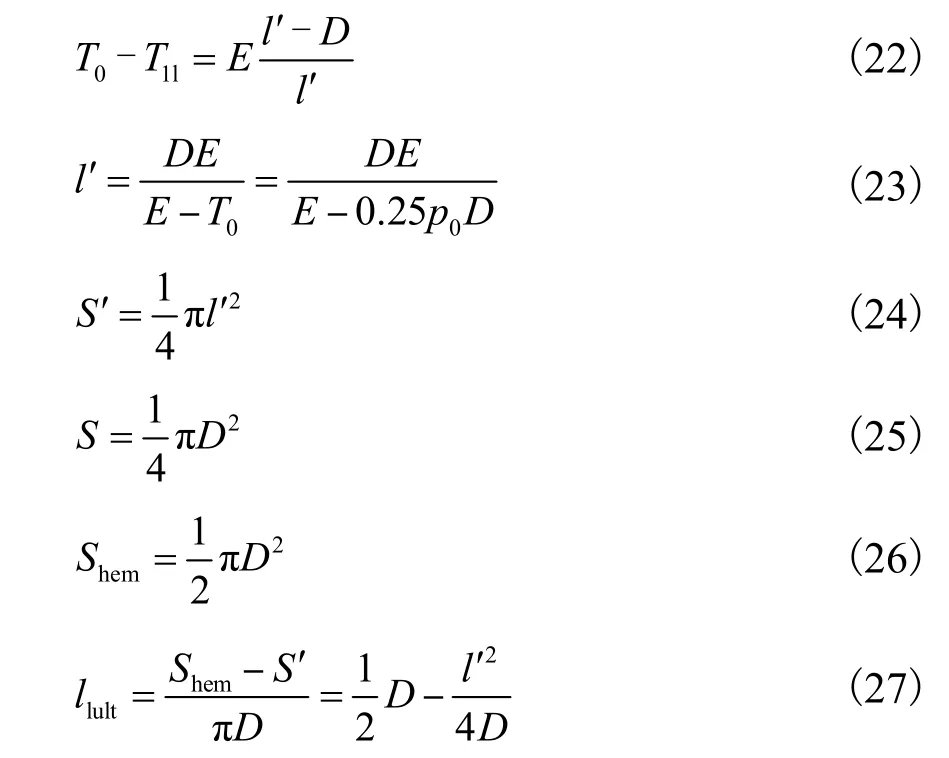
式中：S′为对应于变形为隧道平面面积S的变形前的面积，m2；S为变形后的隧道平面面积，m2；Sham为变形前Ⅰ区半球形的表面积，m2；llult为变形后袋子Ⅰ区每侧增加的贴壁直线长度，m．

2)气囊自由端的形状及受力分析

气囊受荷后，气囊自由端在内压作用下，半球形气囊拉伸成一个高为lr圆柱体的侧表面和一个新的半球体表面积，如图6(b)所示．

当外压pw等于内压p1时，自由端直线段增加量最大为lrult，如图 6(c)所示．根据胡克定律，长度lrult计算过程见式(28)～式(32)．

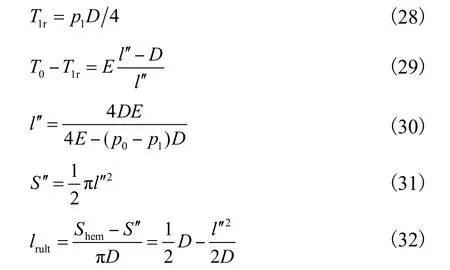
3)气囊直线段受力分析

气囊极限状态时直线段长度lz计算过程见式(33)～式(35)．

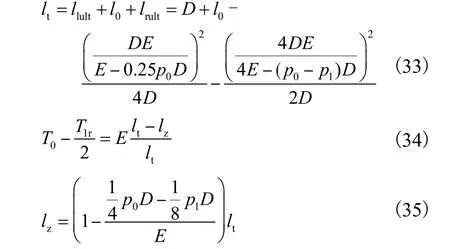
1.3.4 气囊极限状态时的内压分析

根据对三维状态下气囊受荷端、自由端以及直线段部分的分析，可确定气囊在极限状态的形状和受力．根据气体状态方程式(1)，与式(36)、(37)联立可求得极限状态气囊内压p1，也是气囊可承受外压的最大值，以此作为气囊设计的依据之一．

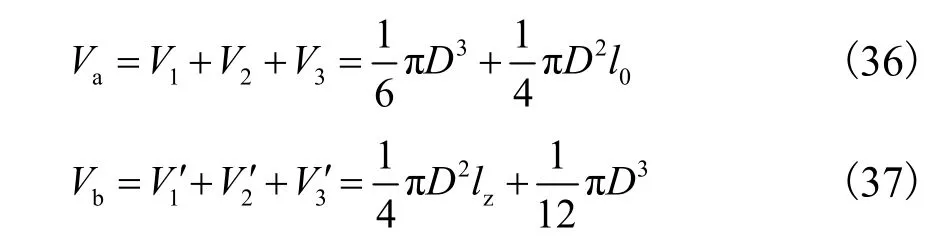
1.3.5 气囊整体受力分析

以上关于气囊的变形和受力分析是基于气囊与管壁不产生相对滑动为前提的，故需使气囊与管壁的最大静摩阻力大于外部荷载(见式(38))，极限状态时气囊在隧道中的水平向受力分析如图7所示，可以得到气囊能够抵挡的最大荷载pwult．

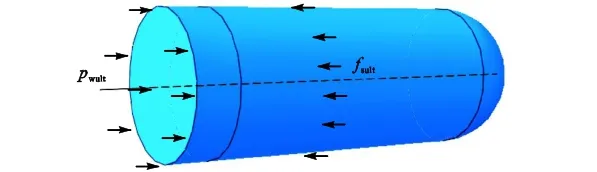
图7 气囊极限状态时的水平向受力分析Fig.7 Horizontal force analysis of rubber airbag in limit state

1.4 气囊正常工作的控制条件

根据以上对气囊在外压作用下的受力和变形分析，可知保证气囊稳定有效地工作而不发生滑动的 3个控制条件，而且必须同时满足．本文分别用二维和三维模型推演了一系列理论公式，并针对3种控制条件分析两种模型的差异和优劣，为气囊设计及应用提供依据．

(1) 外压pw不能大于气囊变形后的内压p1．变形后的内压p1的大小除了与初始内压有关，最重要的是取决于气囊变形前后的体积比，由式(17)、式(18)和式(36)、式(37)可知，当气囊长径比和初始内压相同时，二维计算出的内压p1略大于三维计算结果，达到极限状态时，能够抵挡的外压也较大．但两者差值不大，如图 8所示，当E＝3,kN/m时，差值在3%,左右，随着E增大，两种模型计算的差值逐渐减小至一个定值．

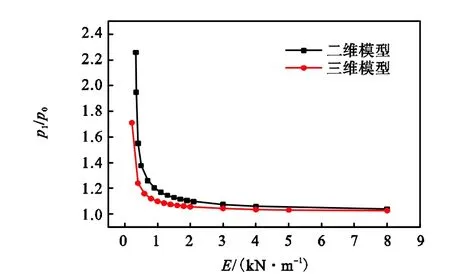
图8 p1/p0与E的关系Fig.8 Retation between p1/p0 and E

(2) 外力不能大于气囊与隧道壁的最大静摩阻力．由式(20)和式(39)可知，二维计算得到的可抵挡的最大外荷载pwult小于三维结果，接近一半左右，采用二维模型设计气囊长度时结果偏于保守．

(3) 气囊张力不能大于材料的抗拉强度．由式(9)和(28)可知，二维计算得到的气囊自由端张力大于三维结果，接近 2倍左右，用二维计算结果进行气囊材料选择时结果偏于保守．

三维工况更接近实际情况，但在气囊长度和材料强度选择时应考虑一定的安全储备，而二维的计算结果偏于保守，且计算较为简洁，两种模型可供设计人员根据不同情况选择使用．

2 气囊拉伸模量对变形的影响

本文研究的是弹性气囊在隧道中的变形及保持稳定的控制条件，气囊的拉伸模量对其伸缩性和受荷载之后的变形影响非常大，而气囊的变形直接影响变形后内压的增长值、摩擦段的长度以及材料的张拉力，从而影响气囊的阻漏能力，因此研究气囊拉伸模量的变化对气囊各形状参数和内压值的影响十分必要．

以初始直线段长度 0.5,m、直径 0.1,m、初始内压为 6,kPa的气囊为例，分别通过二维、三维模型研究当拉伸模量变化时，气囊在其极限状态时形状参数和内压的变化规律．

2.1 拉伸模量对内压p1/p0的影响

极限状态的内压p1与初始压力p0的比值p1/p0表示气囊受荷之后内压的增长值，将其与气囊材料拉伸模量E的关系绘制于图8．

由图 8可知，当拉伸模量较小时，在外压作用下气囊的内压增长值大，其极限状态能抵挡的外压也大；当模量较大时，气囊内压增长微小．故伸缩性好的气囊在同等初始内压情况下可以抵挡更大的外压，同等条件下，二维计算结果较大．

2.2 拉伸模量对llult/l0的影响

将橡胶膜拉伸模量E和受荷端增加的直线段长度llult与初始长度l0的比值llult/l0的关系绘制于图9．

图9 llult/l0与E的关系Fig.9 Relation between llult/l0 and E

由图 9可知，当拉伸模量较小时，在外压作用下气囊受荷端增加的直线段为负值，是由于初始的半圆形在卸压收缩后较短，不足以构成极限状态的形状，需初始的直线段共同参与才收缩至一条直线．当模量较大时，气囊Ⅰ区除构成极限状态的直线外，多出的部分llult增加了直线段的长度，也增大了抵抗荷载的能力．当模量处于曲线与x轴的交点时，初始的半圆形恰好构成极限状态的直线，此时直线段的增长量为 0．

2.3 拉伸模量对lrult/l0的影响

将橡胶膜拉伸模量E和自由端增加的直线段lrult与初始长度l0的比值lrult/l0的关系绘制于图10．

由图 10可知，拉伸模量越大，在相同压力下，lrult/l0的值越小；当拉伸模量趋近无穷时，lrult/l0趋近于零，即自由端保持不变形．

图10 lrult/l0与E的关系Fig.10 Relation between lrult/l0 and E

2.4 拉伸模量对lz/l0的影响

将橡胶膜拉伸模量E和最终的直线段长度lz与初始长度l0的比值lz/l0的关系绘制于图11．

图11 lz/l0与E的关系Fig.11 Relation between lz/l0 and E

由图 11可知，当拉伸模量位于曲线与x轴的交点左侧时，lz/l0＜1，即极限状态时直线段长度小于初始长度；反之，则大于初始长度，而气囊抵抗滑移的摩阻力大小与直线段长度有关，故变形后的气囊抵抗外压的能力增强．

2.5 拉伸模量对Vb/Va的影响

将橡胶膜拉伸模量E和极限状态的体积Vb与初始体积Va的比值Vb/Va的关系绘制于图12．

图12 Vb/Va与E的关系Fig.12 Relation between Vb/Va and E

由图12可知，当拉伸模量越大，Vb/Va的值越大，即体积收缩量的越小，当拉伸模量无穷大时，比值趋近于一个稳定值．

3 模型试验

3.1 试验介绍

为研究气囊在外压作用下的变形特性、气囊内压增长规律以及其阻漏失稳的控制条件，并验证上文所述理论公式的适用性，进行小比尺模型试验．试验采用透明有机玻璃管模拟隧道，选用拉伸模量较小的材料模拟气囊，使其变形更为显著，以便观察记录．隧道模型长1,m，内径0.1,m，右端封闭并与加压系统相连，以提供侧压力，左端敞口，如图 13所示．试验分别用不同长度的气囊，充气至不同的内压，进而在右侧施加外压以证明理论规律的普适性，两个压力表分别测量外压和气囊内压．

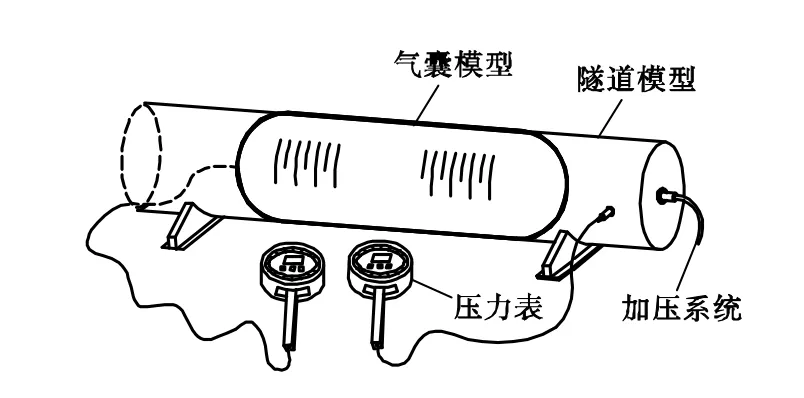
图13 弹性气囊堵气模型试验Fig.13 Model test of plugging rubber airbag

3.2 试验过程

步骤1测量气囊材料的拉伸模量E＝0.35,kN/m.

步骤 2测量气囊材料与隧道模型即有机玻璃的摩擦系数μ＝0.48．

步骤3将长度为35,cm的橡胶囊放在隧道模型中，充气加压使其初始内压为 6.47,kPa后停止加压．在气囊右侧加均匀的压力，使外压从 0逐步增大，记录其形状的变化和内外压增长的规律，直至气囊产生滑移堵气失效为止．

步骤4将上述橡胶囊初始内压充至7.28,kPa，按步骤3重复进行试验．

步骤5将长度为49,cm的橡胶囊充气使其初始内压为3.7,kPa，按步骤3进行试验．

3.3 试验结果

3.3.1 气囊内压和外压的增长规律

1) 情况 1：L＝35,cm，p0＝6.47,kPa

长度为 35,cm 的气囊，初始内压为 6.47,kPa，然后施加外压并逐步增大，将内压、外压随时间的变化曲线绘制于图14中．由图可知，在第1阶段，内压随外压增大而增大，外压由零增长至最大值 8.8,kPa，气囊内压随之由6.47,kPa增长至9.22,kPa，内压增长量Dp＝2.75,kPa，内压达到最大表明气囊处于即将滑动的极限状态．在第 2阶段，内压和外压均发生突降，这是因为气囊在外压作用下向左发生滑动，导致气囊右侧空间瞬间增大，外压迅速减小，而气囊形状也暂时得以恢复，体积有所增大，因而内压也有一定降低．在第 3阶段，由于气囊滑动在气囊与管壁之间产生微小空隙，继续加压就产生漏气现象，外压无法继续增大，故外压与内压均维持在一个较为稳定的状态，此时外压与内压之比大约维持在0.95左右，这与前文提出外压不能大于内压，当外压趋近于内压时，气囊即将产生滑动的理论，基本一致．

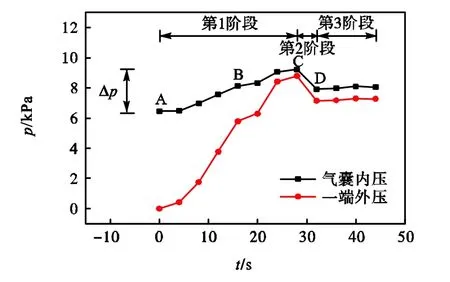
图14 情况1下气囊内压与外压随时间的变化Fig.14 Changes of inside and outside pressures of airbag with time under No.1 condition

2) 情况 2：L＝35,cm，p0＝7.28,kPa

将气囊的初始内压充至 7.28,kPa，内压和外压随时间的变化如图15所示．

由图 15可知，当初始内压不同时，气囊极限状态时能达到的最大内压p1也不同，相应能够抵挡的外压也不同，但气囊受荷变形的阶段和规律基本一致，且极限状态时内压p1的增长规律以及外压与内压的比例均符合上文的理论公式，计算值如表1所示.

图15 情况2下气囊内压与外压随时间的变化Fig.15 Changes of inside and outside pressures of airbag with time under No.2 condition

3) 情况 3：L＝49,cm，p0＝3.70,kPa

将长度为 49,cm的气囊充至 3.70,kPa，内压和外压随时间的变化如图16所示．

图16 情况3下气囊内压与外压随时间的变化Fig.16 Changes of inside and outside pressures of airbag with time under No.3 condition

由图 16可知，当材料长度不同时，气囊受荷变形的阶段和规律基本一致，且极限状态时内压p1的增长规律以及外压与内压的比例也符合上文的理论公式，计算值如表1所示．表中δ为极限状态时理论与试验内压的误差值，即

表1 气囊内压和外压的试验值和理论值Tab.1 Test and theoretical values of the inside and outside pressures of airbag

由表 1可知，当同一个气囊初始内压不相等时，初始内压越大，气囊极限状态的内压也越大．二维计算得到的极限内压比三维结果偏大，图8也能说明二维计算结果较大，当模量E增大时，两者的差别逐步缩小．两者与试验值的误差δ也都保持在10%,以内，说明利用理论公式可以较好地预测气囊内压的增长量．试验中极限状态时气囊的外压与内压之比pw/p1分别为0.954和0.901，也与理论的结论一致．

由表 1还可得，对于长度不同的气囊，内压增长规律以及内外压的增长关系是一致的，这说明理论研究对各种工况均是适用的．同时说明，当气囊长度达到一定程度时，单纯增加气囊长度并不能提高抵挡外荷载的能力．

3.3.2 气囊形状变化规律

在图14气囊内压和外压随时间变化过程中选取4个时刻(A、B、C、D)，将相应时刻气囊的形状对比于图 17中，图 17(a)～(c)与理论假设的气囊变形过程(见图6(a)～(c))一一对应．

图17 气囊形状的变化Fig.17 Change of rubber airbag shape

由图17(a)可以看出，气囊在A时刻，外压为0，在内压的作用下两端呈半球形；随着外压增长，气囊右侧受荷端半圆球逐渐被挤扁，即曲率半径逐渐变大，圆弧顶点向左移动，气囊Ⅱ区部分基本保持不动，气囊左侧自由端半圆球向左移动，如图 17(b)所示．C时刻对应于气囊内压达到最大值的时刻，气囊右端十分扁平，近似接近于平面，气囊左端向左突出明显，此为气囊受荷的极限状态．从 A时刻到 C时刻，气囊的形状发生变化，但其直线段部分未发生滑动，超过 C时刻后，气囊在外压作用下不能保持形状，产生滑动，图17(d)为滑动后的位置和形状，气囊整体向左运动明显．因此，由图 17可知，气囊形状变化规律与前文理论分析有很好的一致性，气囊受荷端由半球形逐渐被挤压至扁平，自由端始终保持半球形，但顶点向左移动明显，当外压接近内压时，气囊堵气失效产生滑动．

根据式(38)可知，此模型试验气囊与管壁间的最大静摩阻力远远大于气囊滑动时受到的外力，气囊滑动失效的原因在于外压接近内压导致形状不能保持，即第1个控制条件不能满足导致的滑动失效．

4 结 论

气囊在隧道中受到外压作用后，其变形特性和保持稳定的控制条件是解决其应用问题的核心．本文考虑材料的拉伸特性，建立了弹性气囊的受力分析模型，从而得到气囊自开始变形至极限状态的过程中变形规律和内压增长的计算公式．同时，进行理论分析得到气囊保持稳定的3个控制条件．采用模型试验对气囊变形特性和阻漏控制条件进行验证，试验结果与理论分析得到的规律有很好的一致性．主要结论有以下4点．

(1) 本文建立的气囊受力分析模型可以很好地体现气囊在隧道中受到外力作用后的形状变化以及变形特性．受荷端处于卸荷呈扁平状态，自由端处于加荷呈鼓胀状态．

(2) 隧道中气囊由于自身特性和约束条件限制，其失效的机理不同于一般结构，气囊保持稳定不滑动、不损坏的控制条件有 3个：外部侧压不能大于气囊变形后的内部压力；外力不能大于气囊与管壁间的最大静摩阻力；材料张力不能大于气囊材料的抗拉强度．

(3) 模型试验中气囊形状的变化以及内外压关系与理论模型一致，证明理论分析的正确性．在模型试验中气囊是外压接近内压导致的形状不能保持而滑动失效．

(4) 气囊材料的拉伸模量对气囊变形影响较大．气囊材料拉伸模量越小，气囊体积的变化量越大，极限状态时能达到更大的内压，对提高抵抗外压的能力有益，但同时气囊直线段长度大大减小，气囊可提供的摩阻力减小，对抵抗外压不利，需根据具体工程选择适当的材料，以达到阻漏的最佳效果．

［1］ 王遇国. 岩溶隧道突水灾害与防治研究[D]. 北京：中国铁道科学研究院，2010.Wang Yuguo. Study on Scourge and Prevention of Karst Tunnel Water Inrush[D]. Beijing: Scientific Research on Chinese Railways，2010(in Chinese).

［2］ Inouye R R，Jacobazzi J D. Great Chicago flood of 1992[J].Civil Engineering—ASCE，1992，62(11)：52-55.

［3］ 王军辉，周宏磊，韩 煊，等. 北京市地下空间运营期主要水灾水害问题分析[J]. 地下空间与工程学报，2010，6(2)：224-229.Wang Junhui，Zhou Honglei，Han Xuan，et al. Analysis of the primary water disasters and water harms in Beijing underground space during operation period[J].Chinese Journal of Underground Space and Engineering，2010，6(2)：224-229(in Chinese).

［4］ 侯贵保. 太原市地铁 2号线工程对地下水环境的影响分析[D]. 太原：太原理工大学，2016.Hou Guibao. Analysis on the Effect of the Groundwater Environment of Taiyuan Metro Line No.2 Project[D].Taiyuan：Taiyuan University of Technology，2016(in Chinese).

［5］ 魏兴萍，张 虹，苏程烜. 重庆南山隧道工程涌水隐患研究[J]. 中国岩溶，2016，35(1)：74-80.Wei Xingping，Zhang Hong，Su Chengxuan. Chongqing Nanshan tunnel water gushing hazard research[J].Carsologica Sinica，2016，35(1)：74-80(in Chinese).

［6］ Martinez X，Davalos J，Barbero E J，et al. In fl atable plug for threat mitigation in transportation tunnels[C]//Proceedings of the Society for the Advancement of Material and Process Engineering Conference.Baltimore，Maryland，USA，2012：21-24.

［7］ Sosa E M，Thompson G J，Barbero E J，et al. Friction characteristics of confined inflatable structures[J].Friction，2014，2(4)：365-390.

［8］ Sosa E M，Thompson G J，Barbero E J. Testing of fullscale inflatable plug for flood mitigation in tunnels[J].Transportation Research Record：Journal of the Transportation Research Board，2014，2407：59-67.

［9］ 江庆海. 地下管道施工及疏通维修工程气囊封堵施工技术[J]. 黑龙江科技信息，2013(22)：258.Jiang Qinghai. Airbag plugging construction technology of underground pipeline construction and dredging maintenance engineering[J].Heilongjiang Science and Technology Information，2013(22)：258(in Chinese).

［10］ 王惠英. 带压封堵技术在大孔径管线上的应用[J]. 石油化工技术与经济，2010，26(1)：41-43.Wang Huiying. Application of in-line plugging technique in large aperture pipelines[J].Technology & Economics in Petrochemicals，2010，26(1)：41-43(in Chinese).

［11］ 靳亚兵，卢立文. 充气式橡胶堵漏器在水利工程堵漏中的应用[J]. 科技视界，2012(28)：429-430.Jin Yabing，Lu Liwen. Application of inflatable rubber stopper in hydraulic engineering[J].Science & Technology Vision，2012(28)：429-430(in Chinese).

［12］ 张国森，钟振利，金敏康，等. 气囊封堵法在排水管道施工及维修工程中的应用[J]. 市政技术，2011，29(3)：72-74.Zhang Guosen，Zhong Zhenli，Jin Minkang，et al. Application of air-bag occlusion method in construction and maintenance of drainage pipeline[J].Municipal Engineering Technology，2011，29(3)：72-74(in Chinese).

［13］ 李 明. 关于气囊堵水技术在超大口径给排水管中的应用探讨[J]. 广东科技，2012(3)：108-109.Li Ming. Application of plugging gasbag in large diameter pipeline[J].Guangdong Science & Technology，2012(3)：108-109(in Chinese).

［14］ 张 建，杨庆山，李 波. 气枕式充气膜结构形态与受力分析[J]. 哈尔滨工业大学学报，2008，40(12)：2020-2023.Zhang Jian，Yang Qingshan，Li Bo. Form-state and loading analysis of air-flated cushion membrane structures[J].Journal of Harbin Institute of Technology，2008，40(12)：2020-2023(in Chinese).

［15］ 余 龙，李 尧，夏利娟，等. 船用气囊力学特性及极限承载力分析[J]. 上海交通大学学报，2014，48(8)：1072-1077.Yu Long，Li Yao，Xia Lijuan，et al. Mechanical property and ultimate bearing capacity of ship airbags[J].Journal of Shanghai Jiao Tong University，2014，48(8)：1072-1077(in Chinese).

［16］ Yan S W，Chen J，Sun L Q. Methods for designing partially inflated geotubes[J].Journal of Marine Science& Technology，2016，24(1)：1-9.