基于差别矩阵的属性集求核算法
2018-03-08张贤勇
杨 涛, 张贤勇,2, 冯 山
(1.四川师范大学 数学与软件科学学院 四川 成都 610066;2.四川师范大学 智能信息与量子信息研究所 四川 成都 610066)
0 引言
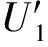
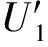
1 基本概念

定义1[4]决策表信息系统S=(U,C,D,V,F)中,b∈C,如果POSC(D)=POSC-{b}(D),则称b为C中相对D不必要的;否则,称b为C中相对D必要的.C中所有必要属性的集合称为C相对D的核,记为coreC(D).
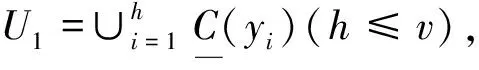
命题1coreC(D)={α(α∈C)∧(∃mij((mij∈IDM)∧(mij={α})∧mij=1))}.
定义2表明,差别矩阵算法求不相容决策表信息系统中核属性时,首先将论域U中所有对象分为完全相容子论域U1与完全不相容子论域U2,其次将U1中对象两两比较,并将U1中的对象与U2中的对象两两比较,最后根据命题1从差别矩阵中找出简单属性(单个属性).
2 基于差别矩阵的属性集求核算法
2.1 差别矩阵的空值
根据定义2可知,差别矩阵求解核属性时会出现空值,这些空值元素的出现会占用大量存储空间,使得求核属性浪费了大量计算时间.因此,提出一种压缩差别矩阵的构造方法.
定理1(空值优化) 在决策表信息系统S=(U,C,D,V,F)中,记相容子论域U1={x1,x2,…,xk}.当∀xi,xj∈U1∧F(xi,D)=F(xj,D)时,则忽略对象xi,xj的比较运算.
证明因∀xi,xj∈U1(1≤i≠j≤k),所以信息系统S中,∀b∈C存在如下关系:①F(xi,b)=F(xj,b);②F(xi,b)≠F(xj,b).由定义2知,当∀xi,xj∈U1,F(xi,d)≠F(xj,d)时,mij={b∈CF(xi,b)≠F(xj,b)},否则,mij=∅.因此,差别矩阵中的空值与条件属性值的取值无关;显然,当∀xi,xj∈U1∧F(xi,D)=F(xj,D)时,忽略对象xi,xj的比较运算.
算法1空值优化执行过程.
输入: 决策表S=(U,C,D,V,F);输出: 可以忽略比较的对象.
步骤1 得到完全相容子论域U1与完全不相容子论域U2,记U1={x1,x2,…,xU1};
步骤2 L=∅;//L用于收集U1中可以忽略比较的对象;
步骤3 for (i=1;i for (j=2;j≤U1;j++) if(F( xi,D)=F(xj,D)) L=L∪{xi,xj}; 步骤4 输出L. 算法1以决策表信息系统中的决策属性值D为划分依据,将论域U划分成相容子论域U1与不相容子论域U2,然后对U1中的对象按照决策属性值的不同划分成多个对象集,进而减少当决策属性值相同时的不必要计算,同时也压缩了差别矩阵中空值元素.一般情形下,算法1的时间复杂度为O(U12).在实际应用中,上述算法虽然有2个循环,但是内循环在循环过程中,当对象xi与xj可以忽略比较,对象xi与xk(k≠j)可以忽略比较时,由传递性可得对象xj与xk可以忽略比较.因此,算法在执行过程中减少了内循环次数,即算法1的时间复杂度为O(U1). 在决策表信息系统S中,若∀b∈C,xi,xj∈U1,F(xi,b)=F(xj,b)∧F(xi,D)=F(xj,D)成立,或∀b∈C,xi,xj∈U2,F(xi,b)=F(xj,b)∧F(xi,D)≠F(xj,D)成立,则利用差别矩阵算法求得的属性集相同,这不但占用大量存储空间,而且也浪费了大量计算时间. 定义3(决策表化简) 在决策表信息系统S=(U,C,D,V,F)中,定义新决策表S′=(U′,C,D,V′,F′).信息函数F′满足:F′(xi,C)=F(xi,C),d∈D且 进而,F′自然确定U′与V′. 根据定义2可知,当∀xi∈U1,xj∈U2时,mij≠∅.当∃xk∈U2∧F(xk,C)=F(xj,C)∧F(xi,d)≠F(xj,d)成立,则mij=mik.又因xj,xk∈U2,根据定义2可知mjk=∅.故在利用差别矩阵求解核属性时,当∀xj,xk∈U2时,将U2中具有“相同条件属性值但不同决策属性值”的对象进行合并不影响核属性的求解结果.在决策表S′中,∀xi,xj∈U′,b∈C,均有mij 定理2当mik⊂mjk∧mjk-mik=1∧{(xi,xj)F(xi,b)≠F(xj,b)}=∅,∀b∈mik时,mij=mjk-mik∧mij=1. 根据定理2可知,当mik∩mjk=∅时,显然mij={mik∪mjk}∧mij≥2.定理2揭示了核属性集的关系,即在对象xi,xj比较之前,先判定属性集mik与mjk是否满足数量之差为1.若为1,则判定mik⊂mjk是否成立.因mik,mjk中的属性集合是有序的,因此判断mik⊂mjk时,其时间复杂度为max(O(mjk)). 其中:“—”表示无需考虑比较的对象. 算法2基于差别矩阵的属性集求核算法. 输入:决策表信息系统S=(U,C,D,V,F);输出:决策表信息系统的核coreC(D). 步骤1 执行算法1; 步骤2 根据定义3创建新的决策表S′; 步骤3 coreC(D)=∅,core1C(D)=∅,core2C(D)=∅; for (r=1;r≤C;r++) if (F(xi,cr)≠F(xj,cr)) 执行定理2; 步骤7 coreC(D)=core1C(D)∪core2C(D); 步骤8 输出coreC(D). 通过比较可知,本文算法的时间和空间复杂度均低于文献[6]和文献[7]所提算法的时间和空间复杂度. 表1 决策表S 表2 化简后的决策表S′Tab.2 Simplified decision table S′ 在表2基础上,根据定义4方法构建差别矩阵SIDM,如表3所示.分析差别矩阵SIDM可知coreC(D)={c1,c2}. 如果采用文献[6]方法创建差别矩阵IDM为5×8规模,如表4所示,共有40个元素;如果采用文献[7]方法创建差别矩阵IDM′为4×5规模,如表5所示,共有20个元素.采用本文方法创建的差别矩阵SIDM为2×4规模,实际存储的元素为7个.可见采用本文方法既减少了样本对象的个数,又降低了差别矩阵的空间占用,从而减少了数据的处理量,提高了求核效率.事实上,基于表1和表2,“表4→表5→表3”的改变过程清楚地体现了“文献[6]→文献[7]→本文”3种算法的差别矩阵改进过程. 表3 差别矩阵SIDM 表4 差别矩阵IDM 表5 差别矩阵IDM′ 采用文献[7]中使用的UCI数据集(http://archive.ics.uci.edu/ml/datasets.html),在Intel(R) Core(TM) i5-2400 CPU @ 3.10 GHz、RAM 2 GB环境下,对文献[6]、文献[7]与本文算法进行了比较.UCI数据集及其特征如表6所示,其中U/C表示按照条件属性集C划分后等价类的数目;IDM、IDM′、SIDM分别表示文献[6]、文献[7]以及本文算法差别矩阵实际存储元素的个数.可以看出,本文算法创建的简化差别矩阵中所存储的元素数目SIDM要少于文献[6]和文献[7]差别矩阵中存储的元素个数. 表6 UCI数据集及其特征 图1与图2分别给出3种算法在4种UCI数据集上执行时间与执行空间的比较.基于图1,本文求核算法的执行效率要优于文献[6]和文献[7]的求核算法,并且随着样本对象的增加,该算法效率更加明显.基于图2,对于不相容决策表(如Patient与Car)和包含重复元素比较多的决策表(如Cancer),本文求核算法在执行过程中对存储空间的需求小于文献[6]和文献[7]. 图1 3种算法执行时间比较Fig.1 Comparison on execution time of 3 algorithms 图2 3种算法执行空间比较Fig.2 Comparison on execution space of 3 algorithms 文献[4]的求核算法不能处理不相容决策表,存在一定的局限性.文献[5]提出了改进算法,并解决了文献[4]算法不能处理不相容决策表的问题,但该算法的时空效率并不太理想.文献[7]则在文献[6]的基础上,对决策表中相同对象合并来提高求核效率.研究发现,利用差别矩阵求解核属性的算法效率还能得到进一步的提高.因此,本文提出了一种基于差别矩阵的属性集求核算法.该算法首先将决策表划分成相容与不相容部分;其次运用定理1找到可以忽略比较的对象,运用定义3化简决策表.算法2给出了基于差别矩阵的属性集求核算法伪码,由此设计的算法的时间与空间复杂度均低于文献[6]和文献[7]的时间与空间复杂度,实验结果表明该算法是有效的. [1] ZHANG C S,RUAN J,TAN Y H. An improved incremental updating algorithm for core based on positive region[J]. Journal of computational information systems,2011,7(9):3127-3133. [2] 钱文彬, 杨炳儒, 徐章艳,等. 基于信息熵的核属性增量式高效更新算法[J]. 模式识别与人工智能, 2013, 26(1): 42-49. [3] 李少年, 吴良刚. 基于邻域信息熵度量数值属性快速约简算法[J]. 计算机工程与科学, 2016, 38(2):350-355. [4] HU X, CERCONE N. Learning in relational databases: a rough set approach[J]. Computational intelligence, 2010, 11(2): 323-338. [5] 叶东毅, 陈昭炯. 一个新的差别矩阵及其求核方法[J]. 电子学报, 2002, 30(7): 1086-1088. [6] 杨明, 孙志挥. 改进的差别矩阵及其求核方法[J]. 复旦学报(自然科学版), 2004, 43(5): 865-868. [7] 杨传健, 姚光顺,马丽生. 改进的差别矩阵及其快速求核算法[J].计算机工程与科学, 2010, 32(3): 78-81.2.2 差别矩阵的属性集求核机理

2.3 属性集求核算法描述
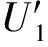
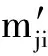
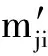
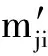
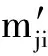
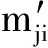
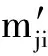
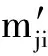
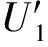
3 实例分析
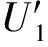




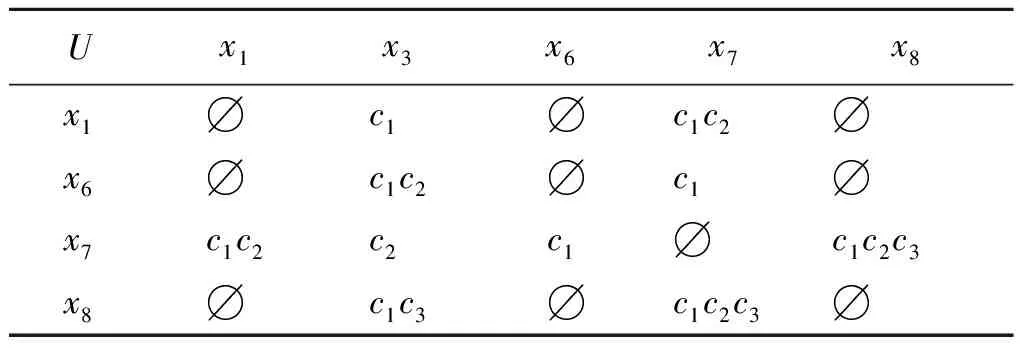
4 实验结果

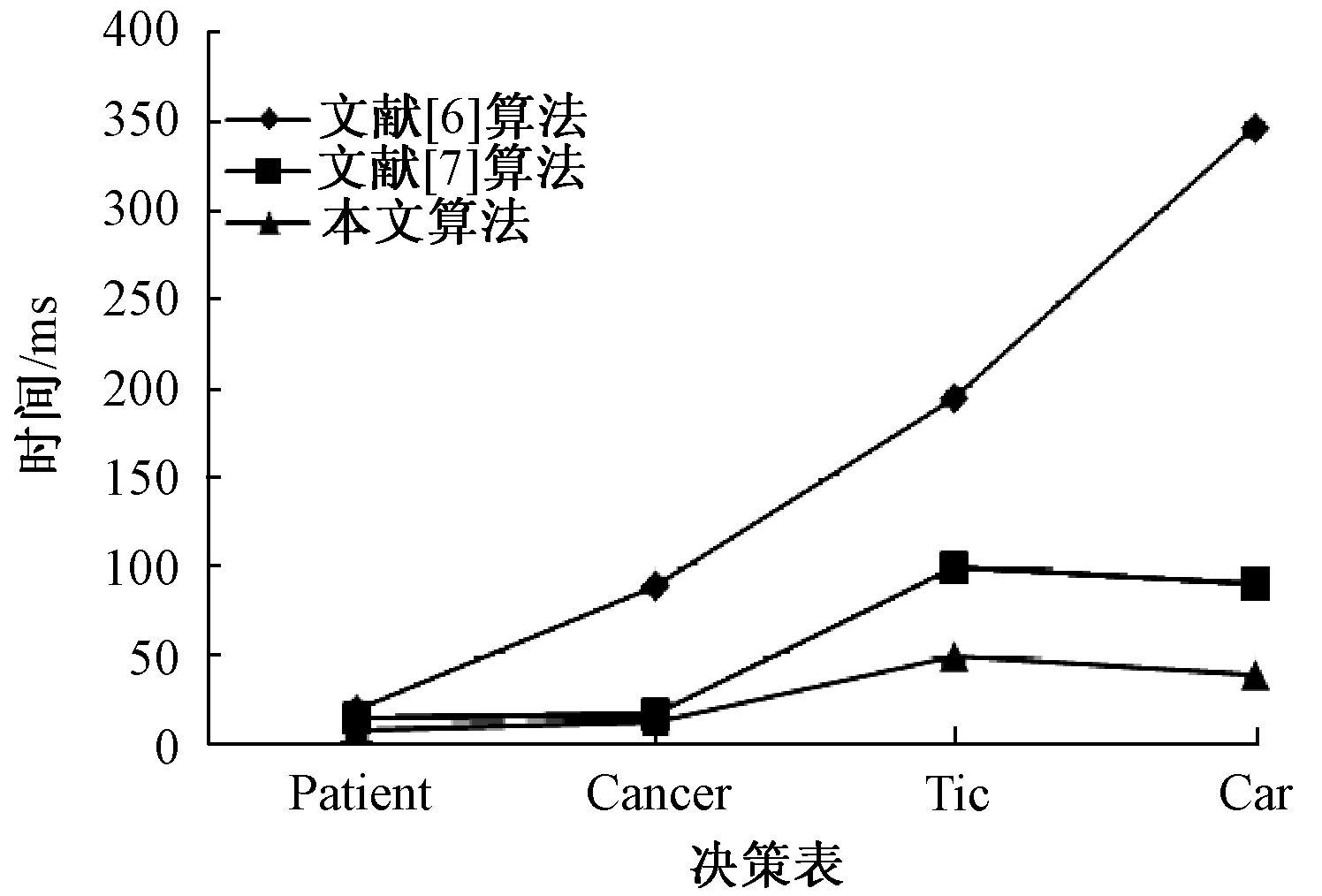
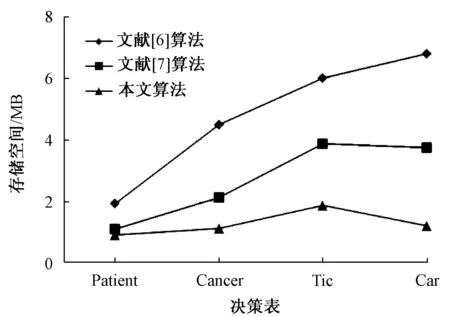
5 结束语
