钢筋笼分料盘链轮轴瞬态动力学分析

王德民，刘荣帅，吴红刚，王鹏宇



钢筋笼分料盘链轮轴瞬态动力学分析

王德民，刘荣帅，吴红刚，王鹏宇

（长春理工大学 机电工程学院，吉林 长春 130022）

钢筋笼分料盘自身惯量大、启动时间短，减速机末端的链轮轴受力复杂，在启动时会承受强大的冲击载荷。利用CATIA软件建立链轮轴的三维模型，并测量分料盘的转动惯量，将计算的动力矩作为瞬态动力学分析的载荷条件，联合ANSYS WorkBench对分料盘链轮轴在启动阶段承受载荷情况有限元分析，得到应力－应变曲线。结果表明链轮轴的强度符合设计要求。

链轮轴；冲击载荷；ANSYS WorkBench；瞬态动力学

钢筋笼具有固聚流质、提高强度的作用，广泛应用于桥梁、高铁及大型建筑物的建造[1]。钢筋笼在焊接过程中，分料盘起到辅助成型、辅助支撑的作用。一套钢筋笼成型机需要1台主动分料盘以及数台随动分料盘设备，主动分料盘通过传动轴带动所有分料盘旋转运动，图1为钢筋笼成型机布局图。考虑到分料盘自身惯量、钢筋重量以及摩擦阻力因素，需要强大的驱动力矩才能使分料盘启动。当焊接工序启动时，会对减速机末端的链轮轴施加瞬间的驱动转矩，使其足以带动所有分料盘的旋转[2]。链轮轴在启动瞬间，要求分料盘在短时间内达到规定的转速，在强大的启动力矩作用下，会对链轮轴产生巨大的瞬间载荷，若链轮轴的强度不足，必然对钢筋笼的焊接质量产生影响，并且造成系统元器件的损坏[3]。利用三维软件CATIA以及有限元仿真软件WorkBench对链轮轴进行瞬间载荷作用下的瞬态动力学分析，保证齿轮轴的强度符合要求，并对后期链轮轴的疲劳寿命分析提供理论参考。

图1 钢筋笼成型机布局图

减速机末端的链轮轴通过键条连接链轮，链轮的齿圈与链轮毂螺栓连接，通过链轮齿圈与链条啮合来传递转矩，链轮布置三个；链条位于铅锤面内，中心线水平，与分料盘轮盘周边轮齿啮合传动转矩[4]，传动示意如图2所示。

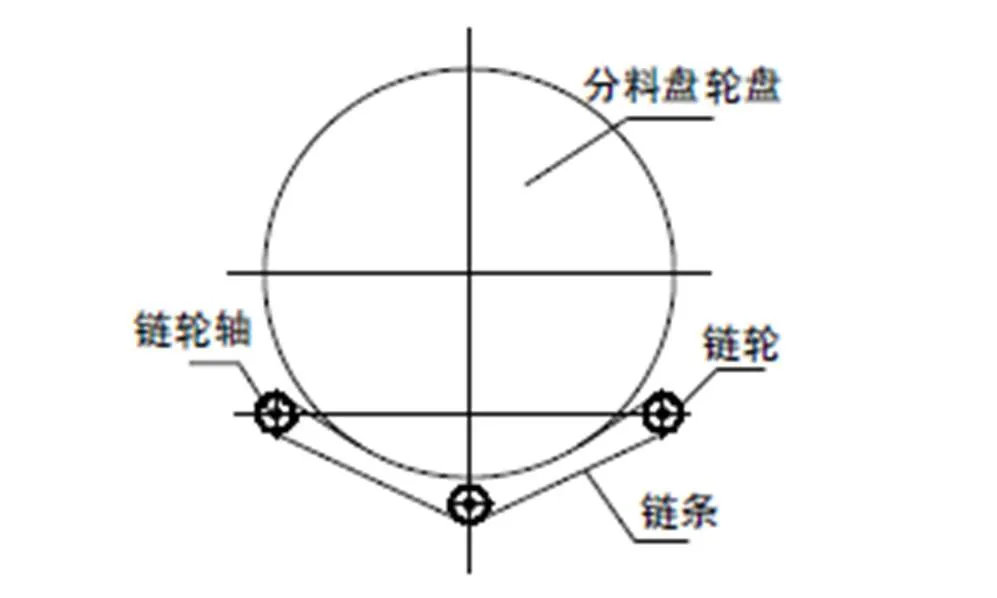
图2 分料盘链传动示意图

1 分料盘启动力矩计算

分料盘轮盘形状呈圆形，但质量分布不均，利用传统数学公式计算繁琐、效率低。本文采用CATIA软件自动计算轮盘的相关参数。首先建立三维模型，加载材料的属性，然后就可测得轮盘的质量及转动惯量等参数。将其作为已知数据即可求相关力矩。

分料盘启动时外界对轮盘产生的阻力矩大，因此在启动时要考虑系统的转动惯量和摩擦力矩，包括转动惯量产生的力矩以及转动时的摩擦力矩[5]。

式中：为启动力矩；M为滚动摩擦力矩；M为转盘以及钢筋转动惯量产生的力矩。

（1）转动惯量包括分料盘轮盘以及轮盘上的钢筋，轮盘的转动惯量直接由CATIA测得为433.65 kg·m2，钢筋的转动惯量计算得37.1 kg·m2，因此转动惯量产生的力矩为：

式中：为轮盘与钢筋的转动惯量之和；为角加速度，其值为0.5 m/s2。

代入参数得：M＝235.375 N·m

（2）摩擦力矩为：

式中：1为分料盘轮盘重量，测得值6838.6 N；2为轮盘上钢筋重量，1644 N；为滚动动摩擦系数，取0.1；为摩擦力作用点距轴心的力臂长。

代入参数得：M＝848.26 N·m

通过CATIA辅助计算，得到一个分料盘的启动力矩为1083.635 N·m，由于主动分料盘带动三个从动分料盘旋转，故总力矩4334.54 N·m。

2 瞬态动力学分析

2.1 瞬态动力学方程

瞬态动力学分析（也称时间－历程分析）用于确定结构承受随时间变化载荷时的动力学响应，使用这种分析方法可得出变载荷作用下结构内部随时间变化的位移云图和应力云图。瞬态分析不同于静态分析，瞬态动力分析主要考虑随时间变化载荷及阻尼和惯性的影响[6]。瞬态动力学分析中求解的运动方程如下：

式中：[]为质量矩阵；[]为阻尼矩阵；[]为刚度矩阵；{}为位移矢量；{()}为力矢量；{}为速度矢量；{}为加速度矢量。

2.2 模型的建立及材料属性设置

利用CATIA建立链轮轴的三维模型，将其保存为IGS格式导入WorkBench 16.0中，如图3所示。链轮轴所用材料为40Cr，杨氏模量206 GPa，泊松比0.3，密度7820 kg/m3，强度极限980 MPa，屈服极限785 MPa。

图3 链轮轴三维模型

2.3 瞬态动力学设置

网格划分的质量对有限元分析结果有较大影响，由于轴的键槽结构，自动划分的方法会在边界产生较多的节点，难以保证计算精度，故采取以六面体为主的划分方法。得到节点数126572个，单元数35968个，如图4所示。

图4 链轮轴网格划分

网格划分完成后，对链轮轴添加约束与载荷。系统启动时，装有链轮的一端是固定的，故加载fix support固定约束；链轮轴另一端受到瞬间力矩，故在另一端的键槽处加载moment力矩载荷[7]。主动分料盘与3个从动分料盘在加速启动阶段的总力矩为4334.54 N·m，由链轮与分料盘轮盘的齿数比17/192可知，加载到键槽处的转矩为383.8 N·m。

齿轮轴瞬态动力学分析的关键是初始时间步长及加载约束的设置。其中时间步长反映了每次求解的叠加时间，决定了求解精度。最小时间步长设置为0.01 s，设置钢筋笼分料盘加速启动的时间为2 s，5 s之后达到钢筋笼正常工作状态（匀速转动）。

2.4 瞬态动力学结果后处理

经仿真分析，链轮轴在启动阶段受到的最大等效应力为490.8 MPa，最大变形量为0.13 mm。应力值并没有达到轴的屈服应力，表明链轮轴强度满足要求，应力图中显示轴肩以及键槽处应力较大，在键槽圆角半径处应力最大。说明过渡圆角处在交变载荷作用下易产生应力集中，应对此位置进行强化处理。由图5和图6中可以看出，在启动瞬间链轮轴要承受分料盘转动惯量以及转动摩擦产生的全部力矩，应力值瞬间达到666.7 MPa。并且由于瞬间载荷，在0.1 s时刻链轮轴瞬间承受转矩增加了66 MPa，随后趋于稳定。

图5 等效应力云图

图6 应力曲线图

3 结论

（1）基于CATIA软件对分料盘链轮轴进行了三维建模，并借助内设工具测得分料盘的转动惯量等参数，进而计算链轮轴受到的驱动力矩，并利用WorkBench 16.0进行瞬态动力学分析。结果表明，链轮轴满足强度要求。

（2）链轮轴在启动瞬间，要求分料盘在短时间内达到规定转速，在自身转动惯量以及摩擦力矩影响下，对链轮轴产生巨大的瞬间载荷，严重影响链轮轴的强度和寿命。因此，在生产要求允许的情况下适当的增加启动时间，减小链轮轴承受的应力，从而更好地保证设备的使用寿命。

[1]叶杨. 钢筋笼盘箍机在建筑工程中的应用[J]. 施工技术，2015（5）：44-46.

[2]石立，张国旺，肖骁，等. 立式螺旋搅拌磨机的启动力矩研究[J]. 矿山机械，2013（7）：68-71.

[3]蓝才武，唐贤明，刁海林. 软启动皮带轮的研究与试验[J]. 广西大学学报（自然科学版），2003（S1）：67-69.

[4]邱宣怀. 机械设计[M]. 北京：高等教育出版社，1997.

[5]任学平，孙百袆，杨松涛，等. 基于SolidWorks与workbench的转炉齿轮轴制动阶段瞬态动力学分析[J]. 机械传动，2014，11（3）：136-139.

[6]任爱华，龚青山，常治斌，郑方炎. 弧面分度凸轮机构瞬态动力学分析[J]. 机械设计与制造，2012（5）：205-207.

[7]许进峰，等. ANSYS Workbench完全自学一本通[M]. 北京：电子工业出版社，2014：140-200.

Transient Dynamics Analysis of Chain Wheel Shaft in Reinforcing Cage Lining Plate

WANG Demin，LIU Rongshuai，WU Honggang，WANG Pengyu

( School of Mechanical and Electrical Engineering, Changchun University of Science and Technology, Changchun 130022, China )

The lining plate of the reinforcing cage is characterized by large inertia and short starting time. The chain wheel shaft at the end of the reducer is complex in force and will bear a strong impact load at the start. This paper established 3D model of chain wheel shaft using CATIA software, measured the moment of inertia of the lining plate and regarded the dynamic torque calculation as the loading condition of transient dynamic analysis, then finite element analysis is carried out to obtain the stress-strain curve of the joint ANSYS WorkBench chain wheel in the starting stage. The results show that the strength of the sprocket shaft meets the design requirements.

chain wheel shaft；impact loading；ANSYS WorkBench；transient dynamics

TH69

A

10.3969/j.issn.1006-0316.2018.02.006

1006－0316 (2018) 02－0023－04

2017－06－16

王德民（1961－），男，辽宁西丰人，本科，副研究员，硕士研究生导师，主要研究方向为机电系统控制与技术。