基于WorkBench的油嘴圆锥螺旋弹簧优化设计
2018-03-07李红艳李东岳
李红艳,李东岳
基于WorkBench的油嘴圆锥螺旋弹簧优化设计
李红艳,李东岳*
(青岛科技大学 机电工程学院,山东 青岛 266061)
根据现有弹簧设计理论以及对弹簧的工作性能要求,利用CAD技术建立合理的弹簧模型。然后利用WorkBench与CAD的无缝对接将弹簧模型导入WorkBench之后对其进行材料定义、网格划分、支反力分析、切应力分析及屈曲分析。通过WorkBench自带的参数设计模块,以弹簧有效长度、弹簧螺距及支反力为变量进行优化设计,将所得结果与传统公式计算结果作对比,最后通过实验验证计算的正确性。
有限元;屈曲分析;圆锥螺旋弹簧
在某些特定的工作状况下对锥形螺旋弹簧的接触压力、并圈压力、屈曲极限等一些工作性能的要求越来越精确,同时,螺旋弹簧的工作条件趋向复杂化,无论是弹簧的轻量化设计,还是在局部的最小化空间的设计,都需要弹簧的优化设计[1],利用WorkBench对其参数进行设计,简单易行,结果合理。
1 三维模型的建立
ANSYS WorkBench自带建模平台Design modeler,还可导入SolidWorks等CAD软件,本文所用锥形弹簧模型是SolidWorks所建,弹簧的大端1圈并圈、小端2圈并圈,利用SolidWorks与ANSYS WorkBench的无缝连接接口,将圆锥螺旋弹簧的数学模型导入ANSYS WorkBench,如图1所示,参数如表1所示。

图1 锥形弹簧模型

表1 弹簧几何参数
材料为70号钢,弹性模量206 GPa,泊松比0.304,切变模量78988 MPa,屈服极限420 MPa。
2 锥形螺旋弹簧的力学计算
圆锥螺旋弹簧的特性如图2所示。当承受载荷后,特性线的段是直线,载荷继续增加时,弹簧从大圈开始逐圈接触,其工作圈数逐渐减少,刚度则逐渐增大,直到所有弹簧压并为止,特性线的段是渐增型,有利于防止共振的发生[2]。

图2 弹簧特性曲线
对图1所示的圆锥螺旋弹簧进行打压实验,如图3所示。对弹簧的实验结果表明,流入打开压力(2~3 MPa)情况下,钢珠能顶开弹簧,使润滑油顺利流入;当打开压力为28 MPa时,弹簧不会破坏或者发生失稳。对弹簧的实验表明,弹簧在线性阶段的刚度为1.83 N/mm。

图3 弹簧油压实验
2.1 理论解
在弹簧圈开始接触前弹簧变形量与弹簧弹力的关系式为:

将模型的参数代入式(1),可以得到在弹簧压缩量为2 mm时弹簧受力为3.668 N,弹簧的刚度为1.834 N/mm。和实验比较发现,计算刚度和实验刚度相对误差为0.2%,所以建立的模型是正确的。
弹簧的切应力为:

计算得到弹簧的切应力为320.27 MPa。
2.2 仿真分析
在使用WorkBench计算分析时,对弹簧小端施加方向2 mm的压缩位移载荷,另一端施加固定约束[3],可以计算得到弹簧支反力,轴向支反力3.562 N,弹簧刚度为1.781 N/mm。
对弹簧施加压缩位移载荷后,弹簧的切应力分布如图4。圆锥螺旋弹簧是扭转和剪切组合变形,弹簧受到压缩作用,压缩产生的切应力沿轴向压缩方向;扭转产生的切应力沿径向线性分布,内侧与压缩方向一致,外侧与压缩方向相反,因此弹簧内侧为应力较大的位置。图4(a)给出轴向压缩2 mm时的切应力分布,最大值为314.71 MPa,位于弹簧内侧,图4(b)为临界并圈时的应力分布情况,两种情况的应力分布规律类似。将仿真结果与解析解比较发现,通过WorkBench计算的结果合理并准确。
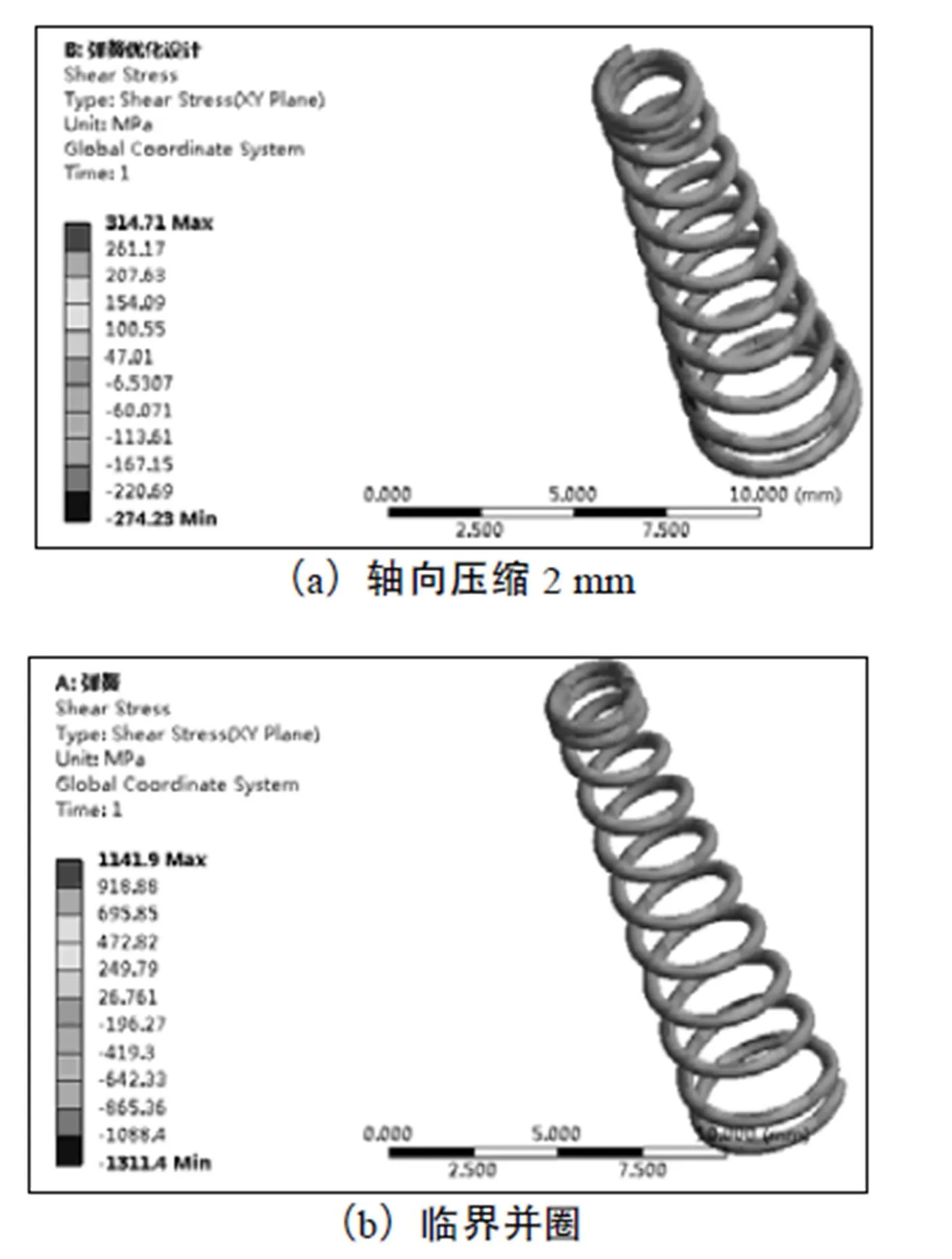
图4 圆锥弹簧的切应力分布(MPa)
3 锥形螺旋弹簧的屈曲分析
压缩螺旋弹簧的侧向屈曲问题在机械工程设计中具有实际意义。细长的螺旋压缩弹簧沿轴向受载时,在加载过程中,当达到某一负荷时,便产生横向变形,即纵向弯曲现象,称为屈曲[4]。线性屈曲分析又被称为特征值屈曲分析,结构的力与位移的表达式为:

式中:[K]为结构刚度矩阵;[K]为几何刚度矩阵;{}为位移向量;{}为载荷向量。
在扰度较小的情况下,[K]与{}为线性关系,{}增加倍时,[K]也增加倍[5],则平衡方程表示为:

假设结构屈曲时达到平衡的虚位移为Δ,则平衡方程变为:

在同时满足式(4)与式(5)情况时有:

由式(6)可推出屈曲判断准则为:

由上可得屈曲分析求解的对象是特征值,得到稳定安全系数即的最小值,临界载荷为0,0为初始载荷。
在WorkBench中有专门的屈曲分析模块,大大简化了屈曲分析的计算。如图5所示。

图5 屈曲分析模块
通过对弹簧施加单位位移载荷可以得到如图6所示结果。

图6 屈曲分析
其中稳定安全系数的最小值为7.606,施加的初始载荷为单位位移载荷,初始载荷产生的支反力0为1.84 N,所以弹簧的屈曲力0为14 N。
4 锥形弹簧的优化设计
设计锥形螺旋弹簧时,除选择材料及规定热处理要求外,主要是根据最大工作载荷、最大变形以及结构要求等来确定弹簧的钢丝直径、有效圈数、节距、螺旋角和高度等参数[6]。通常取、和为优化设计变量。本文通过WorkBench中的优化设计模块以弹簧的有效长度与弹簧螺距为设计变量进行计算。得到结果如表2所示,将计算结果生成3D图如图7所示。
通过图7可以得到弹簧支反力与弹簧有效圈数及弹簧自由高度的关系图,从而进行下一步的参数选取。同样也可以将WorkBench的优化计算应用于弹簧其它参数的计算中。
5 结论
(1)WorkBench计算结果与传统公式计算结果对比表明,有限元仿真技术可以作为弹簧设计人员的设计工具和验证手段,给弹簧设计提供极大的方便,提高设计准确性和效率。
(2)弹簧的稳定性分析是一个比较复杂的力学过程,可以通过WorkBench对弹簧进行屈曲分析,大大减少计算量,后期实验表明计算结果准确。
(3)对于不同的要求,可以将弹簧设计与WorkBench结合起来,利用WorkBench中的优化设计模块进行弹簧参数的计算,快速得到弹簧参数与弹簧弹力的关系,从而选择合适参数。

表2 优化计算

图7 优化计算3D图
[1]孙君钧. 悬架弹簧有限元仿真分析[J]. 金属制品,2015(1):47-49.
[2]机械设计手册编委会. 机械设计手册(第3版)[M]. 北京:机械工业出版社,2004.
[3]杨平辉,何云峰,何志兵. 一种收口螺旋弹簧设计方法[J]. 汽车零部件,2015(5):67-69.
[4]王思年,李清芳. 圆柱螺旋弹簧的屈曲分析[J]. 机械设计与研究,1994(4):13-16.
[5]余娟,余明友,金建伟,宋若愚. 基于ANSYS的天线杆屈曲分析[J]. 计算机与数字工程,2013(9):1523-1524.
[6]石丽娜,曾红,刘淑芬. 基于ANSYS的变刚度螺旋弹簧优化设计[J]. 辽宁工业大学学报(自然科学版),2009(1):44-47.
Optimum Design of Oil Tip Conical Spiral Spring Based on WorkBench
LI Hongyan,LI Dongyue
( Electromechanical Engineering College, Qingdao University of Science and Technology, Qingdao266061, China )
According to the existing spring design theory and our requirements on the performance of the spring, a reasonable spring model is established by using CAD technology. Then, the spring model is introduced into WorkBench by the seamless connection between WorkBench and CAD. Then the material definition, meshing, support force analysis, shear stress analysis and buckling analysis are carried out. And through the WorkBench parameters design module, the optimum design is carried out with the effective length of the spring, the pitch of the spring and the reaction force as the variables. The results obtained are compared with the results of the traditional formula. Finally, the correctness of the calculation is verified by experiments.
finite element;buckling analysis;conical spiral spring
TH135+.1
A
10.3969/j.issn.1006-0316.2018.02.009
1006-0316 (2018) 02-0035-04
2017-06-13
李红艳(1975-),女,山东聊城人,博士,副教授,主要研究方向为有限元分析及应用。
通讯作者:李东岳(1993-),男,山东济宁人,硕士研究生,主要研究方向为有限元分析及应用。
