一种改进的组合定权的指纹定位算法
2018-03-07曹晓祥陈国良
曹晓祥,陈国良,2
(1. 中国矿业大学,江苏 徐州 221116; 2. 国土环境与灾害监测国家测绘地理信息局重点实验室,江苏 徐州 221116)
当前,室外位置服务随着全球导航卫星系统[1](GNSS)的发展日趋成熟,然而对于室内场景,由于GNSS信号衰减与遮挡,GNSS难以满足室内定位需求,因此,对室内定位技术的研究日益受到重视。
许多国内外研究机构、学者基于蓝牙[2]、地磁[3]、射频识别、超宽带[4]、WLAN、计算机视觉[5]和可见光通信[6]等技术在室内定位技术研究上取得诸多成果。这其中WiFi定位技术由于成本低、定位结果可靠,成为研究热点。WiFi定位技术主要包括特殊AP点定位、信号传播模型法、信号指纹定位法。而其中信号指纹定位法由于具有较高的定位精度而被广大学者所关注,大多数在算法简单、易于实现的基于信号空间K最邻近法的WiFi指纹定位算法上进行研究。如刘少伟[7]研究了邻近点K值选取对指纹定位精度的影响;吴赟等[8]利用点位间信号强度余弦相似度作为匹配特性并以此对邻近点进行定权求解坐标,有效解决了终端差异性问题;毕京学等[9]考虑到欧氏距离较小或为0的情况,提出了基于高斯函数定权的KNN室内定位算法;陈国良等[10]通过引入聚类分析方法,对指纹点进行分类预处理,极大地缩短了定位时间;王培重等[11]利用点位间AP的MAC匹配度,提出了一种动态设定K值的定位算法;刘春燕等[12]提出了针对信号不稳定的以几何信息改进基于指纹库的KNN(信号空间K最近邻算法)定位算法。
但是,诸多算法[13-15]均面临同样一个问题:室内WiFi信号的不稳定性,可能会使邻近点匹配出现偏差,一旦匹配出现偏差,将直接影响定位结果,同时也忽视了对邻近点的分布结构的分析,理论上邻近点中心与待定点几何位置具有相关关系。本文就此提出一种改进的组合定权的指纹定位算法,在邻近点匹配结束后,对邻近点几何结构进行分析,剔除偏离邻近点中心较远的点后,再利用选择后的邻近点与其中心点的几何距离、待定点与指纹点欧氏距离组合定权,加权求取坐标,以提高定位精度。
1 WiFi指纹定位算法原理
WiFi指纹定位分为离线指纹点采集和在线定位两个阶段。其中,离线指纹点采集主要工作是采集设计的指纹点处接入点的RSSI信号特征值,通过采集大量指纹点数据构建指纹数据库,其中指纹数据库包含有指纹点位置与该点RSSI序列的映射关系;在线定位阶段将未知点采集的RSSI序列与指纹库中指纹点存储的数据进行匹配,借助相关定位算法,解算得到未知点的位置坐标。其具体内容如图1所示。

图1 WiFi指纹定位原理
当前部分基于最近邻法的WiFi指纹定位算法原理与优缺点比较见表1。

表1 不同WiFi指纹定位算法原理与优缺点
2 改进的基于组合定权指纹定位算法
本文提出的基于邻近点二次选择的指纹定位算法是对WKNN定位算法的改进,对依据待定点与指纹点欧氏距离匹配得到的K邻近点的几何结构进行分析,剔除其中偏离邻近点中心较远的点位后,再将待定点与邻近点欧氏距离、邻近点与K个邻近点中心距离倒数组合,利用WKNN算法中定权方法,使用两个距离倒数之和加权,计算定位结果。具体包括以下几个步骤:
(1) 欧氏距离计算。首先将定位终端扫描的待定点的AP信号强度值与指纹库中每个指纹点的存储数据进行欧氏距离计算,利用欧氏距离确定待定点与指纹点匹配程度,其中欧氏距离计算公式为
(1)
式中,i=1,2,…,n;di表示待定点与指纹库中第i个指纹点之间的欧氏距离;n1表示待定点扫描的AP中与第i个指纹点存储的AP相同的个数;RSSIj为待定点扫描到的第j个AP的信号强度;RSSIij为第i个指纹点扫描到的第j个指纹点的信号强度值;n表示指纹库中指纹点的个数。
(2) 初始邻近点选择。各个指纹点与待定点欧氏距离计算完成后,对距离序列进行排序,得到K个与待定点距离最近的指纹点,即初始K个邻近点。其中K值设定借助试验手段,判断最优K值的选取,一般在单个房间内,K取值为5~8个,或动态地对K值进行判断,选取最优K值。
(3) 初始邻近点几何结构分析。借助式(2)、式(3)分析初始邻近点的几何结构,依据AP发射的信号传播规律,原则上匹配的邻近点应环绕分布于待定点周围,以待定点为中心呈放射状分布,因此可以通过式(3)计算每个邻近点与初始K个邻近点中心的距离,剔除偏离邻近点中心较远的点位,其中具体剔除个数也需借助试验进行动态分析,一般为了保持邻近点的几何结构,剔除个数通常设置为1~2个,另外初始邻近点中心利用式(2)进行计算。
(2)
(3)
式中,xcenter,ycenter,zcenter、(xi,yi,zi)分别表示初始邻近点的中心点坐标和第i个邻近点的坐标;lic表示第i个邻近点与初始邻近点中心的几何距离。
(4) 初始邻近点二次选择。各个邻近点与中心点距离计算完成后,对距离序列进行排序,得到K′个与中心点距离最近的邻近点,K′值的确定由初始邻近点个数K和邻近点剔除个数共同决定。
(5) 距离组合定权。由无线信号传播规律可知,邻近点与待定点的欧氏距离越小,邻近点几何位置与待定点的几何位置关系越大;同样,二次选择后邻近点理论上环绕分布于待定点四周,二次选择后邻近点中心理论上近似与待定点重合。因此,邻近点到中心点的距离在一定程度上反映了其对待定点位置的影响,该邻近点距离邻近点中心越小,其对待定点几何位置影响越大。因此,可结合以上两种距离对待定点位置的影响规律进行组合定权。具体定权方式为
(4)
式中,i=1,2,3,…,K′;pi表示第i个邻近点对定位结果影响权值;K′为邻近点二次选择后的个数。
(6) 加权均值。利用式(4)求得的权值及K′个邻近点坐标,依照下式加权求均值
(5)

3 算法试验及分析
3.1 试验环境
试验场设置在中国矿业大学环境与测绘学院楼四楼A409,其中测试楼道与房间均布设有所需AP,在7 m×9 m房间按1.2 m×1.2 m(由于室内有办公桌椅,并不是严格按照1.2 m间隔取点)格网均匀布置36个参考点,如图2所示。

图2 室内指纹点与测试点分布图
离线指纹点采集阶段,利用自主开发的WiFi指纹点采集与定位软件进行数据采集与定位工作,采集定位界面如图3所示。每个指纹点间隔6 s采集AP信号强度,采集10次,取平均值存入指纹库。如图2所示,在测试房间内选取37个测试点进行静态测试,并建立相对坐标系,用于点位误差检核。

图3 WiFi指纹点采集与定位软件
3.2 试验结果与分析
图4给出某一测试点连续进行60次信号强度采集后,任选其中扫描的4个AP信号强度变化。由图可以看出,室内环境复杂多变,引起AP信号强度变化起伏,在利用邻近点算法时,极易造成邻近点匹配出现偏差,影响定位结果。

图4 某测试点任选4个AP信号强度变化
对30个静态测试点进行定位计算时,初始匹配邻近点个数K设置为7[7],对30个点的扫描结果分别利用KNN算法、WKNN算法及本文改进算法进行处理,比较定位结果并进行分析。
表2是对初始邻近点K值取值进行试验分析的结果,分别对K=3,4,5,…,8的定位效果进行统计。结果表明,当K=5时,误差小于3 m的概率达到94.4%,因此,试验中设计初始邻近点个数为7个,设计邻近点二次选择中剔除个数为2。
图5分别从37个测试点中随机选取23个点,对每个点位利用WKNN算法和本文改进算法得到的定位结果在X轴、Y轴上的误差进行描述,可以看出,不论是X轴,还是Y轴上的定位误差,本文改进算法的误差均小于WKNN算法产生的误差(由于人员走动频繁,个别点位结果较差)。图6则是对两种算法点位误差进行描述,同样,本文改进算法定位效果均优于WKNN算法。

表2 初始邻近点个数K值定位误差概率统计 (%)

图5 WKNN算法与本文改进算法在X、Y轴方向上的误差比较(任选23个测试点)
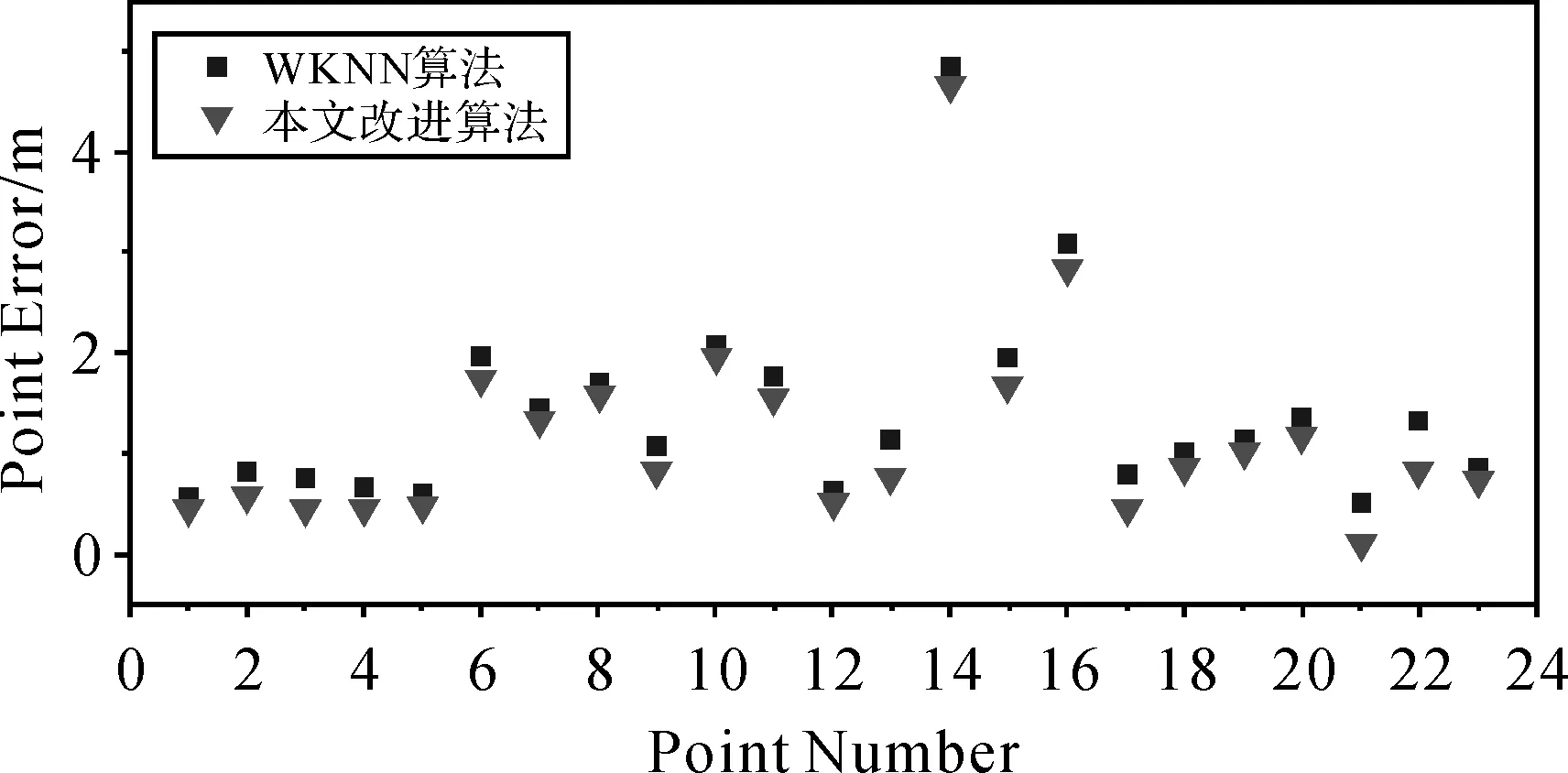
图6 WKNN算法与本文改进算法点位误差比较(任选23个测试点)
从图7可以看出,本文改进算法定位精度优于3 m的概率达到94.6%;另外,WKNN算法和本文改进算法定位精度优于1 m的概率分别为45.9%和56.8%。

图7 定位误差累积概率分布
从表3可以看出,KNN算法、WKNN算法和本文改进算法误差最大值均高于5.3 m,该测试点位于房间边缘,且桌椅遮挡严重,从而导致较大误差。从定位误差均值来看,本文改进算法的定位误差较小,定位效果要优于KNN算法和WKNN算法。
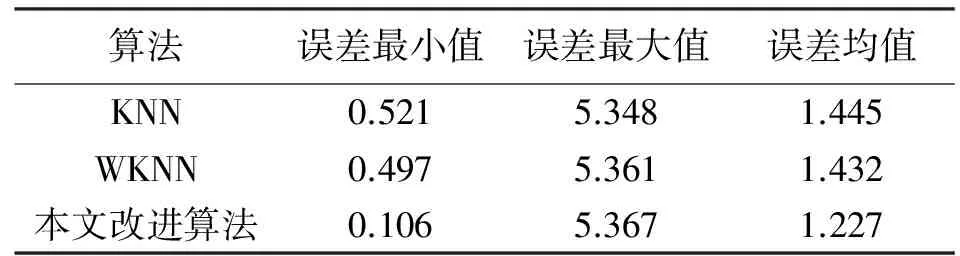
表3 定位误差对比 m
由以上可知,本文改进的基于邻近点二次选择算法相较于KNN算法和WKNN算法虽然增加了部分计算量,但是其定位效果和定位稳定性均有提升。
4 结 语
本文改进的几何距离与欧氏距离组合定权的指纹定位算法是在WKNN基础上,对利用指纹点与待定点欧氏距离匹配得到的K个邻近点几何结构进行分析,剔除邻近点中偏离邻近点中心较远的点位,得到K′个邻近点后,再将待定点与邻近点欧氏距离、邻近点与K个邻近点中心距离倒数组合,利用WKNN算法中定权方法,使用两个距离倒数之和加权求均值。与KNN算法和WKNN算法相比,本文改进算法避免在定位计算中使用匹配出现偏差的点位,提升了定位稳定性和精度。指纹库几何位置边缘定位误差还需进一步研究。
[1] 宁津生,姚宜斌,张小红.全球导航卫星系统发展综述[J].导航定位学报,2013,1(1):3-8.
[2] ZHOU S,POLLARD J K.Position Measurement Using Bluetooth[J].IEEE Transactions on Consumer Electronics,2006,52(2):555-558.
[3] INDOORATLAS.Ambient Magnetic Field-based Indoor Location Technology:Bringing the Compass to the Next Level[EB/OL].2017-09-08.www.doc88.com/p-1187544632856.html.
[4] ZAPATER A,KYAMAKYA K.A UWB-based Indoor Positioning Concept: Problem Formulation,System Design and Feasibility Analysis[C]∥International Conference on Wireless Networks.Las Vegas:[s.n.],2003:114-118.
[5] YAN L,XU Z.Quality Analysis of Vehicle-based Sequence Images Relative Orientation Based on Computer Vision[J].ISPRS-International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2012(XXXIX-B3):443-446.
[6] YOSHINO M,HARUYAMA S,NAKAGAWA M.High-accuracy Positioning System Using Visible LED Lights and Image Sensor[C]∥2008 IEEE Radio and Wireless Symposium.Orlando:IEEE,2008:439-442.
[7] 刘少伟,花向红,邱卫宁,等.WiFi指纹定位中AP个数对定位精度的影响[J].测绘工程,2017,26(2):33-36.
[8] 吴赟,蒋新华,齐雁飞,等.基于加权余弦相似度的WiFi指纹室内定位[J].上海师范大学学报(自然科学版),2017,46(1):124-128.
[9] 毕京学,甄杰,汪云甲,等.高斯函数定权的改进KNN室内定位方法[J].测绘通报,2017(6):9-12.
[10] 陈国良,张言哲,汪云甲,等.WiFi-PDR室内组合定位的无迹卡尔曼滤波算法[J].测绘学报,2015,44(12):1314-1321.
[11] 王培重,郑南山,张言哲.基于动态K值及AP MAC地址筛选的室内定位算法[J].计算机科学,2016,43(1):163-165.
[12] 刘春燕,王坚.基于几何聚类指纹库的约束KNN室内定位模型[J].武汉大学学报(信息科学版),2014,39(11):1287-1292.
[13] GE X,QU Z.Optimization WiFi Indoor Positioning KNN Algorithm Location-based Fingerprint[C]∥2016 7th IEEE International Conference on Software Engineering and Service Science.Beijing:IEEE,2016.
[14] LI D,ZHANG B,LI C.A Feature-scaling-based S|kS|-Nearest Neighbor Algorithm for Indoor Positioning Systems[J].IEEE Internet of Things Journal,2016,3(4):590-597.
[15] LU X,QIU Y,YUAN W,et al.An Improved Dynamic Prediction Fingerprint Localization Algorithm Based on KNN[C]∥2016 Sixth International Conference on Instrumentation & Measurement,Computer,Communication and Control.Harbin:IEEE,2016.
