自动推算室内接入点坐标算法

郑加柱，高业何敏

(南京林业大学土木工程学院，江苏 南京 210037)

突发事件是指突然发生造成或可能造成严重社会危害，需要采取应急处置措施予以应对的自然灾害、事故灾难、公共卫生事件和社会安全事件，具有突发性、危险性、紧迫性和不确定性等特点[1]。在突发事件处理过程中，位置信息是必不可少的，因此基于位置的服务(location based service，LBS)在此过程中起到极为重要的作用[2]。当前，基于位置的服务从服务区域来看主要分为室外定位和室内定位两大部分。有关室外定位的研究已有较长的历史，相关技术(如GPS、北斗等)较为成熟，精度也相对较高[3]。室内定位技术虽起步较晚但也发展迅猛。目前常用的室内定位技术主要有WiFi定位技术、超宽带定位技术、蓝牙定位技术等。综合考虑成本、精度及设备等因素，WiFi定位技术在室内定位领域应用得最为广泛[4]。

目前基于WiFi的室内定位技术主要有两种方式[5-8]：第一种是利用接收的信号强度指示(received signal strength indication，RSSI)值的指纹数据库实现定位；第二种是通过测量待定点与多个WiFi 接入点(access point，AP)之间的RSSI值，通过距离交会定位算法进行定位。而无论哪一种WiFi定位技术，都需要预先知道室内AP的坐标信息。当突发事件发生时，并不是所有的室内场景都满足这样的条件以便迅速处理突发事件，而且预先获得室内AP的坐标信息这一工作增加了人力物力，未从根本上实现自动化。因此，本文针对这一问题，提出了一种基于M估计的自动推算室内AP坐标的算法。该方法只需在室内外交界处同时获取卫星定位信息和WiFi 信号的RSSI值，再利用优化后的RSSI测距算法和距离交会算法，即可快速、较准确地获得WiFi 接入点AP坐标。

1 理论基础

1.1 RSSI基本测距理论

基于RSSI的测距是一种廉价的测距技术，一般情况下，接收的平均功率随着距离的增加而成指数衰减，可用对数路径损耗模型描述[9]。

P=P0+10×n×lg(d/d0)

(1)

式中，P0为在距离AP为d0处接收到的RSSI值，一般情况下取d0为1 m；P为在距离AP为d处接收到的RSSI值；n为与环境相关的路径逸散系数，环境不同，n值不同。

这种测距技术精度较低，需要通过算法的改进，以获得更高的测距精度。

1.2 距离交会定位原理

距离交会定位是常用的定位方法[10-11]，设在室内外交界处有1、2、3这3个位置，在这3个位置上分别获取这3个位置的坐标及与同一个AP之间的距离，其信息集合为(X1,Y1,Z1,d1a)、(X2,Y2,Z2,d2a)、(X3,Y3,Z3,d3a)，再设AP点的坐标为(Xa,Ya,Za)，则可组成下列方程组求解AP点坐标

(2)

实际应用此原理定位时，为确保获得较高点位精度，需要在每个位置上多次获取该点坐标，采用最小二乘算法，求解待测点坐标。但当测量结果中含有粗差时，最小二乘解将不是最优解，因此也需要对该原理的算法进行改进。

2 算法改进

2.1 基于均值滤波的RSSI测距算法改进

在绝对理想的条件下，接收器接收AP的平均功率随着距离的增加而成指数衰减，但实际情况下，由于环境及收发器本身的干扰非常多，如收发天线的类型和方向、信号衰减和多路径影响、任何电器产生的电磁噪声等，这些因素都会对RSSI值的测量产生影响[12]，这导致了实测RSSI值与距离并不完全满足理论上的函数关系，因此，需要对RSSI测距算法进行适当的改进。为此，选定距AP点1 m、2 m、…、12 m这12个位置，在每个位置上测定100次RSSI值，绘制成折线图如图1所示。

根据实际观测的RSSI值，利用式(1)和经验数据，可确定取d0=1 m时，P0=-46；n取1.5，从而得到RSSI与距离d之间的关系为

P=-46-16×lgd

(3)

(4)

图1 实际RSSI测量值折线图

由于WiFi 信号易受外界条件影响，其稳定性差，这样采用RSSI观测值的众数计算出的距离值比平均值计算出的距离值精度更高，可靠性更好[13]，因此求出12个位置处的RSSI观测值众数分别代入式(4)，计算出12个位置与AP的距离。将观测的距离减去实际距离定义为RSSI测距误差，其结果见表1。

表1 实测RSSI值众数及测距误差

由表1可以看出，当观测距离增加时，RSSI测距误差剧烈增加，这是由于观测距离增加时，由于环境干扰因素增多、信号衰减剧烈增加，路径逸散增大，为减小这种影响，本文采用分段RSSI测距算法，即利用分段函数对不同的RSSI观测值采用不同的路径逸散系数为

(5)

当观测到的RSSI值小于等于阈值-70时，采用较大的路径逸散系数，当观测到的RSSI值大于阈值-70时，采用较小的路径逸散系数。将上述试验观测得到的RSSI值众数代入式(5)，解算出RSSI测距误差，其结果列入表2。改进后的RSSI测距算法与原RSSI测距算法，测距误差比较如图2所示。

表2 实测RSSI值众数及分段测距误差

图2 两种算法误差比较

由表2和图2可以看到，运用分段RSSI测距算法大大降低了远距离处的测距误差。

2.2 残差绝对和最小的M估计

考虑室内定位技术的普及需要在移动终端上使用，因此本文利用手机自带的GPS和WiFi功能，同时获取某点三维坐标以及其到AP点的RSSI信号强度值。由于手机定位精度有限，粗差不可避免地存在于GPS观测数据中，而且由图1可以看出手机测得的RSSI值浮动较大，偏离正常值较大的观测值也可被认为是粗差。如果利用最小二乘处理这种包含了粗差的观测数据，即使粗差个数不多，仍将严重歪曲参数的最小二乘值，影响成果的质量。

稳健估计的基本思想是：在粗差不可避免的情况下，选择适当的估计方法，使参数的估值尽可能避免粗差的影响，得到正常模式下的最佳估值。M估计又称为极大似然估计，是稳健估计在测量界应用最为广泛的一种[14-16]。

(6)

用ρ( )代替-ln f( )，则M估计准则可改写为

(7)

由此可见，有一个ρ函数就定义了一个M估计。残差绝对和最小的M估计，其ρ函数为

ρ(u)=u

(8)

本文采用残差绝对和最小的M估计对推算的AP坐标进行稳健估计处理，以抵抗GPS观测过程中可能存在的粗差，提高推算的AP坐标精度。

3 试验与分析

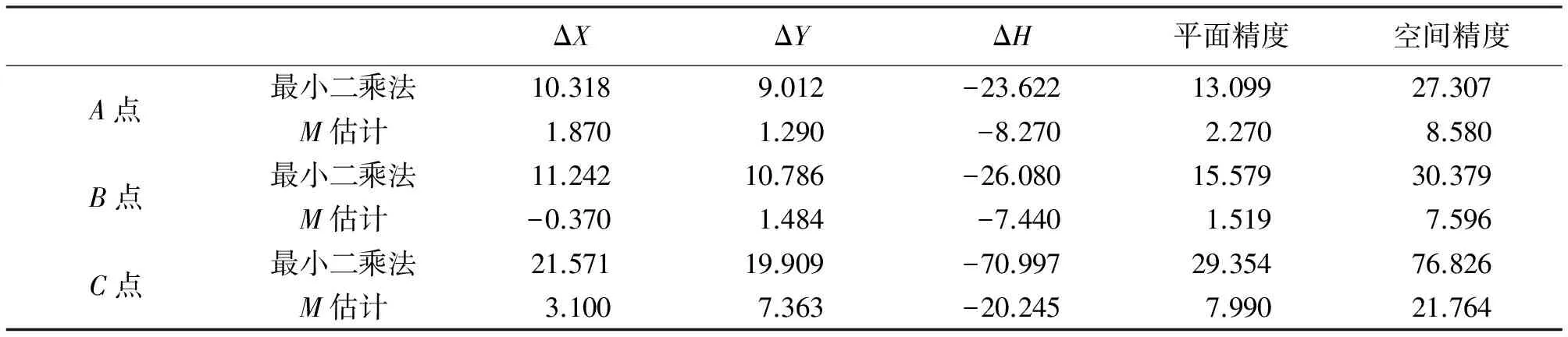
如图3所示，2-A、A-B、B-C分别相距4 m，在室外1、2、3已知点处分别以每秒一次的频率获取10次坐标信息及与A、B、C3处AP之间的RSSI信号强度值信息。对获取的RSSI值利用式(5)进行分段RSSI测距处理。利用解算得到的距离值及观测得到的坐标信息，根据式(2)采用最小二乘法求出室内区域内A、B、C这3点的坐标，再对三点的坐标值进行残差绝对和最小的M估计处理。处理后的结果及其精度对比见表3。

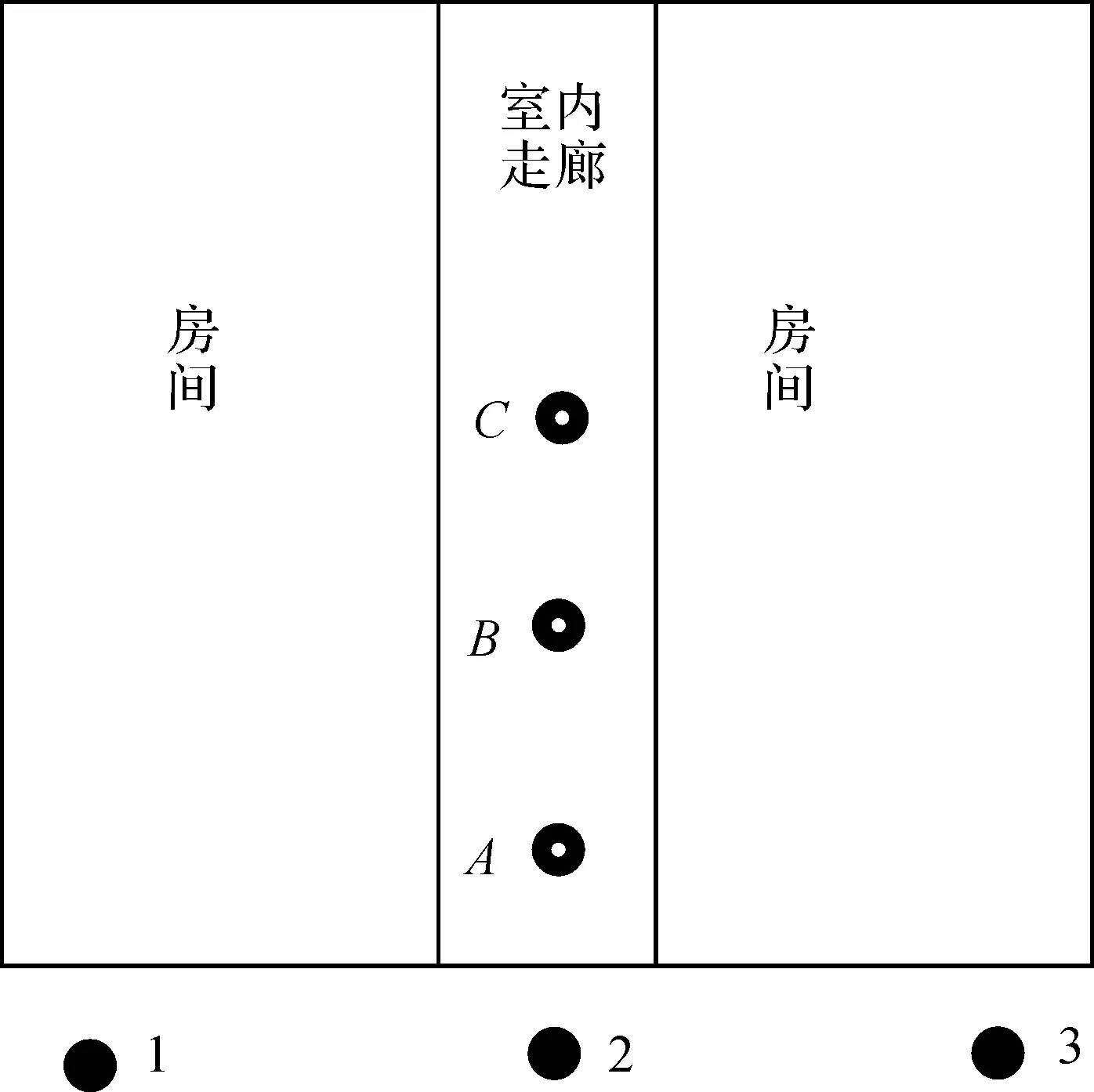
图3 试验场景示意图

m

由表3可见，在距离室外2号点4 m处的A点，经残差绝对和最小的M估计解算后得到的平面精度和空间精度分别为2.27和8.58 m，相比于同位置处最小二乘算法解算出的坐标，精度分别提高了82.6%和68.6%；在距离室外2号点8 m处的B点，经残差绝对和最小的M估计解算后得到的平面精度和空间精度分别为1.519和7.596 m，相比于同位置处最小二乘算法解算出的坐标，精度分别提高了90.2%和75.0%；距离室外2号点12 m处的C点，经残差绝对和最小的M估计解算后得到的平面精度和空间精度分别为7.99和21.764 m，相比于同位置处最小二乘算法解算出的坐标，精度分别提高了72.8%和55.1%。

4 总结与展望

本文提出了将分段RSSI测距与基于M估计改进的距离交会定位结合进行室内AP坐标推算的算法，弥补了长距离情况下由于环境干扰多、信号衰减快等原因导致的RSSI测距误差急剧增大的缺点；利用残差绝对和最小的M估计对手机获取GPS坐标可能存在粗差及RSSI值变化不稳定进行处理，有效减小粗差及RSSI值不稳定对推算坐标的影响，从而进一步提高坐标推算精度。试验证明，基于M估计的室内AP坐标推算算法能够有效地推算出三维坐标，对于室内较远处的AP，其推算精度也较好。但目前该算法对于高程推算方面精度略低，未来将着重研究提高高程的精度。

[1] 李岳德,张禹.突发事件应对法立法的若干问题[J].行政法学研究,2007(4):69-75.

[2] 党安荣,王丹,梁军,等.中国智慧城市建设进展与发展趋势[J].地理信息世界,2015，22(4):1-7.

[3] 庄春华,赵治华,张益青,等.卫星导航定位技术综述[J].导航定位学报,2014，2(1):34-40.

[4] 裴凌，刘东辉，钱久超.室内定位技术与应用综述[J].导航定位与授时,2017，4(3):1-10.

[5] 陈斌涛,刘任任,陈益强,等.动态环境中的WiFi指纹自适应室内定位方法[J].传感技术学报,2015，28(5):729-738.

[6] 蔡炒晖,夏溪,胡波,等.室内信号强度指纹定位算法改进[J].计算机科学,2014，41(11):178-181.

[7] CHAN E C L，BACIU G，MAK S C.Using Wi-Fi Signal Strength to Localize in Wireless Sensor Networks[C]∥Communications and Mobile Computing，WRI International Conference on.[S.l.]：IEEE，2009.

[8] 靳超，邱冬炜.基于WiFi信号室内定位技术的研究[J].测绘通报,2017(5):21-25.

[9] 万国峰,钟俊,杨成慧.改进的RSSI测距和定位算法[J].计算机应用研究,2012,29(11):4156-4158.

[10] 彭雪生,花向红,邱卫宁,等.一种WiFi距离交会加权融合定位算法[J].测绘工程,2017,26(2):72-75.

[11] 李桢,黄劲松.基于RSSI抗差滤波的WiFi定位[J].武汉大学学报(信息科学版),2016,41(3):361-366.

[12] 方震,赵湛,郭鹏,等.基于RSSI测距分析[J].传感技术学报,2007,20(11):2526-2530.

[13] 陈国良，张言哲，汪云甲，等．WiFi-PDA室内组合定位的无迹卡尔曼滤波算法[J]．测绘学报，2015，44(12)：1314-1321.

[14] MUKHOPADHYAY B，SARANGI S，KAR S.Novel RSSI Evaluation Models for Accurate Indoor Localization with Sensor Networks[C]∥Communications(NCC)，2014 Twentieth National Conference on.[S.l.]：IEEE，2014：1-6.

[15] 邱卫宁,陶本藻,姚宜彬,等.测量数据处理理论与方法[M].武汉:武汉大学出版社,2008.

[16] 沈云中,陶本藻.实用测量数据处理方法[M].北京:测绘出版社，2012.