基于ODR-BADASYN-SVM的中小企业信用风险评估

2018-03-07孟杰李田苑泽明

金融发展研究 2018年1期

孟杰李田苑泽明

（天津财经大学商学院，天津300222）

一、引言

融资难一直制约着中小企业的发展。中小企业在初始成长阶段无法积累足够的内部留存，加之多层次的资本市场尚未形成，使得信贷融资成为中小企业早期获得资本支持的主要途径。然而，信息不对称、有效抵押品不足等，致使银行为规避风险而考量的贷款条件极为“苛刻”，从而导致信贷配给；特别是在信贷市场以大型银行为主导的我国，中小企业融资难这一世界性难题就显得格外突出（郭娜，2013）。对中小企业信用风险进行评估，能够使外部投资者了解企业实际信用状况，避免由于道德风险与逆向选择造成的损失，以进一步优化融资环境。

近年来，随着人工智能与数据挖掘技术的发展，具有较高准确性与适用性的机器学习模型被用于企业信用风险评估。支持向量机（Support Vector Mechine，以下简称SVM）作为其中一种基于统计学习理论的机器学习方法，由于在处理小样本、高维度以及非线性数据时优点突出，逐渐被用于信用风险的评估。

本文采用文献调研与问卷调查相结合的方法，构建中小企业信用评估的指标体系；在此基础上，选取A股上市非金融公司中的中小企业数据作为研究样本，利用SVM模型对中小企业信用风险进行评估；为解决非平衡样本对模型性能的影响这一问题，利用ODR-BADASYN方法对模型进行改进，并以非均衡样本分类的Gmean和Fmeasure指标对模型性能进行评价，利用T检验对模型间性能的差异性进行检验。评估结果发现，改进后的SVM模型在中小企业信用风险评估方面具有较高稳定性和预测能力，能够为投资者判断中小企业信用风险进而开展贷款决策提供依据。

二、文献回顾

（一）信用风险评估及其方法

信用风险评估是指对待评估主体可能引起信用风险的各种定性、定量的指标进行分析或计算，从而测度借款人违约的概率，为贷款与否提供决策依据（张目等，2009）。信用风险评估是信用风险管理的基础和关键。

自Beaver（1966）首次提出以单一财务比率评价公司信用风险以来，信用风险评估方法随着技术进步日益丰富，目前可以分为因素分析法和模型分析法（沈凤武等，2012）。

因素分析法主要基于企业的财务因素或信用要素。其中，财务因素分析法的考察内容较为单一，主要包括比率分析法、趋势分析法及比较分析法等。信用要素分析法在财务因素的基础上，将影响企业信用的要素纳入指标体系，主要包括“5C”、“5W”和“5P”等方法。尽管信用要素分析法在一定程度上弥补了前者指标单一的不足，但由于存在内容接近、判断主观、结果受主客观影响明显等问题（张玲等，2000），应用程度尚不及模型分析法。

随着统计知识在经济学科的深入应用，模型分析法得到逐步发展和广泛引用，多元线性模型、Logit模型、KMV模型及以神经网络模型为代表的非参数机器学习模型等（丁欣等，2002）均属于该范畴。Altman等（1968）利用美国破产企业与非破产企业的财务指标，构建风险判别函数，率先使用多元判别分析方法进行风险评估；其后不断完善评价指标，建立了Zate信用评分模型（Altman等，1977），但由于应用条件较为苛刻（如要求数据本身服从正态分布且满足协方差矩阵相等），限制了模型在实际应用中的效果。Ohlson等（1981）构建了以Logistic函数为基础的Logit判别模型，在对企业违约概率进行实际验证的基础上，证明了其结果优于多元线性模型。该模型随后与主成分分析相结合，以探索最佳主成分指标的选取（Aguilera等，2006），提升模型的评价能力。Dong G等（2010）在比较不同模型的作用后，分析了Logit模型的优点，同时为提高模型精度加入随机系数，实现了对信贷风险的有效管理。考虑到各财务指标之间存在错综复杂的网络结构关系，方匡南等（2016）构建了基于网络结构的Logit模型，并应用于企业信用风险预警。然而，囿于样本量需求大以及财务指标之间的多重共线性问题，Logit模型的应用也受到局限。

KMV模型在上市公司信用风险评价中的应用得到肯定（蒋彧等，2015；牛晓健等，2012）。结合中国金融市场的特点，蒋彧等（2015）对KMV方法进行了修正，并运用于我国上市公司的信用风险评估，认为修正后的KMV在特定条件下具有较好的评估能力。但由于该模型假设评估指标严格服从正态分布，并且只有通过对比分析才能得出企业违约的概率，影响了模型准确性，KMV模型在中小企业信用风险评估中的应用受到局限。

以神经网络为代表的非参数有监督学习模型是随着人工智能技术发展而出现的一类模型评价方法。吴德胜等（2004）在研究中引入遗传算法和BP神经网络构建GA-BP模型，评估我国商业企业信用风险，以克服传统网络训练中局部极小的缺点，但这种BP神经网络模型在处理小样本、高维度数据时，精确度往往有所降低。

（二）SVM模型原理及其改进

SVM由Vapnik和Corinna Cortes于1995年首先提出，是一种基于Mercer定理、以结构风险最小化为原则的机器学习模型。相对其他模式识别方法，SVM结合了理论驱动、易于分析的统计方法与数据驱动、灵活的机器学习方法的优点（Viaene S等，2002），能很好地解决样本数量少、维数高及非线性等实际问题（Yu L等，2005；Mitsdorffer R等，2008）。在样本量小的情况下，SVM方法分类的准确性优于多元判别法，进而为银行等投资者判断信用风险提供依据（唐建荣等，2010）。并且在这种情况下，SVM方法能够得出特征空间的最优解，通过分类准确率这一指标评价模型性能，发现其与神经网络方法相比更优，在信用风险评估中的作用更显著（Viaene S等，2002；杨毓等，2006；李云飞，2008）。

然而，相对正常企业的数量，实际存在信用风险的企业数量少，两类样本间的不平衡性会影响SVM的预测结果，使得SVM预测准确率降低，且降低幅度会随样本不平衡性的增加而增加（李扬等，2016）。提升SVM对不平衡样本预测性能，可通过样本的过采样和欠采样，进行数据层面的改进。其中，针对少数类样本过采样的SMOTE方法，可以通过人工生成一定量的少数类样本来提高SVM模型的分类能力（Gong M G等，2006；Chawla N等，2002；王超学等，2014）。但SMOTE方法忽视了少数类样本的分布特点，容易造成样本重叠，且存在无法处理多数类样本的缺点（林宇等，2016）；由此，林宇等（2016）提出自适应抽样合成方法（ADASYN）与逐级优化的欠采样方法（ODR）来改进SVM模型。此外，针对ADASYN方法合成的新样本分布分散、不能抵抗孤立样本和噪声样本干扰等问题，洪铭等（2017）提出了改进的BADASYN算法，只对处于边界区域的少数类样本进行自适应合成。

（三）文献述评

现有研究表明，相对于因素分析法而言，模型分析法的评估结果更加客观、有效；而模型分析法中，SVM在评估企业信用风险方面具有显著优势。此外，针对研究样本存在的不平衡性，可以通过数据层面的方法改进，有效克服样本处理中的缺陷，提高模型的性能。借鉴已有研究，本文在利用文献调研和问卷调查构建风险评估指标体系的基础上，首次提出采用ODR与BADASYN相结合的方法，对SVM模型进行性能改进，并率先将该模型应用于中小企业信用风险评估，为中小企业的贷款决策提供依据。

三、模型设计

（一）SVM模型

SVM的本质是一种算法，基本思路是求解最优分类面，即在特定空间求解能够将样本准确分类，并使得不同样本间的分类间隔最大的最优分类面。具体来说，在样本线性可分时，SVM在样本空间求解最优分类面；在样本线性不可分时，SVM便通过内积核函数对样本进行内积运算，将其投射到高维空间模拟线性可分的情形求解最优分类面。距离最优分类面最近的训练样本被定义为支持向量，其他训练样本对定义分类界面无关（Cristianini N.等，2000；Gunn S R，1998）。

对于中小企业来说，信用状况的评价可以分为正常企业和违约企业两类。设yi∈{1，-1}为指标变量，定义当yi=1时，第i个企业为正常企业；当yi=-1时，第i个企业为违约企业。同时定义xi=(xi1,xi2,…,xin)为测度第i个企业违约与否的特征变量，最终得出由特征变量与指标变量共同构成的样本点(xi，yi)0≤i≤N。在样本点()xi，yi线性可分时，样本空间判别函数的一般形式为f(x)=w*x+b，可以得出相应分类面方程w*x+b=0，其中w是可调权值向量即分类超平面的法向量，b为分类阈值。对f(x)进行归一化处理，使得对于任意xi都满足||f(xi)≥1，求出两类支持向量间的分类间隔为2/‖w‖。SVM求解最优分类面以使‖w‖最小的问题就可以转化为有约束条件的优化问题：

在样本点线性不可分时，SVM引入松弛变量ξi构建软间隔，允许误判样本的存在。同时引入惩罚因子C以使2/‖w‖尽可能大，尽可能小，进而使分类尽可能准确，这时有约束条件的优化问题转化为如下形式：

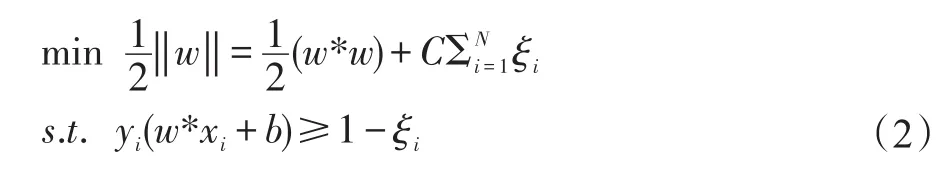
同时，当样本点线性不可分时，可以通过运用内积函数将样本空间投射到高维空间，在高维空间求解最优分类面。利用拉格朗日乘子将上述求解最优分类面的问题转化为对偶问题

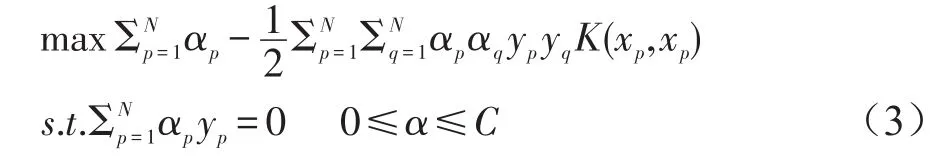
这里α是拉格朗日乘子，K(xp,xp)是引入的内积核函数。通过对此二次规划问题求解，可以得出最优分类函数为：

（二）提升SVM性能的ODR-BADASYN方法

本文引入ODR和BADASYN算法，通过对正常企业样本逐级优化欠采样和违约企业边界样本过采样，提升SVM在不平衡数据样本的中小企业信用风险评估中的性能。

定义训练样本集为T，其中多数类正常企业样本集为N，少数类违约企业样本集为P，n表示正常企业样本集N中的样本，p为违约企业样本集P中的样本，并定义某一样本关联集为样本集中该样本的K个最邻近样本和该样本本身组成的样本集。流程中步骤1—6是ODR算法，重点在于删除正常企业中的噪声样本；步骤7—12是BADASYN算法，重点在于合成违约企业边界样本。算法最终调整原非均衡数据，为SVM提供平衡的训练样本，提升模型的预测性能（见表1）。

（三）模型评价指标

本文所讨论的中小企业信用风险评估模型是建立在非均衡样本基础上的分类器，用以判断平衡样本分类结果的分类准确率难以科学地评价模型预测能力，尤其是对违约企业样本的预测性能（李扬等，2016）。在实际工作中，违约企业被错分的代价往往大于正常企业被错分的代价。因此，本文采用评判模型对于非均衡样本分类性能的指标，即几何平均正确率Gmean（以下简写为G）和少数类的Fmeasure（以下简写为F）来评价模型的性能。指标具体构建过程如下：

定义|TN|和|FN|分别为被正确划分为正常企业和被错误划分为正常企业的样本数量，|TP|和|FP|分别为被正确划分为违约企业和被错误划分为违约企业的样本数量。由此得出违约企业样本正确率（灵敏度）SE、正常企业样本正确率（特异度）SP、违约样本企业查准率P：

表1：算法流程描述

其中，G权衡了多数类正常企业样本和少数类违约企业样本对模型性能的影响，对于其中任何一类有所偏移的最优分类面都会影响另一类样本的分类结果及准确率，使得G变小；相反，如果模型对于两类样本的预测精度高，则G会变大。少数类的F指标则将少数类违约企业样本灵敏度与查准率相结合，衡量对违约企业的预测效果，F越大则预测效果越好，模型性能越优。

四、样本选择及指标选取

（一）样本选择

本文参考梁琪（2014）的做法，以A股上市非金融公司中的中小企业数据作为研究样本，中小企业划分标准按照工业和信息化部等四部委《中小企业划型标准规定》和国家统计局《统计上大中小微型企业划分办法》。将财务失败与否作为评判企业是否存在信用风险的标准，选取了2007—2015年首次被证监会实施特殊处理（ST）的中小企业样本，剔除数据缺失样本后剩余113家。同时以年份、行业为基础，以从业人员、资产规模与营业收入三个维度为标准，选取配对非ST中小企业样本共387家，样本不平衡度为3.42：1。

（二）指标选取

在信用风险评估中，对能够甄别企业存在信用风险与否的指标的确定起着重要作用。基于现有研究，本文设计并向科研机构、高校、金融机构等发放问卷415份，回收有效问卷354份，以确定用于企业信用风险评估的财务业绩与非财务业绩两大指标体系（见表2）。

1.财务业绩指标。本文选取了企业偿债能力、营运能力、盈利能力、成长性、资本结构和财务杠杆、现金流状况以及资本市场表现等7个方面的33个财务业绩指标。为保证财务业绩指标能够较好地预测企业信用风险，也为了区分两类样本（正常企业与违约企业）的特征，对两类样本财务业绩指标做了独立样本T检验，得出两类不同样本指标在5%水平上差异显著的共21个。

2.非财务业绩指标。本文基于国内外学者关于企业信用风险与财务失败等方面的文献检索，从多个角度分析了表征企业信用风险的要素，即通过实际控制人类型、董事会特征、股权结构和市场指标等4个方面的信息来衡量非财务业绩的指标对企业信用风险的影响。

（1）实际控制人。Friedman等（2003）将企业的利益传输分为向上传输的隧道效应与向下传输的支持效应，其中隧道效应是指企业的最终控制人通过各种方式侵占企业利益的行为。梁琪等人（2009）研究了企业财务失败预警中实际控制人的控制权与所有权因素的影响，认为控制权与所有权水平高的控制人会通过影响公司治理或者财务业绩进而对企业财务预警结果造成影响。本文选取所有权性质指标描述实际控制人类型。

（2）董事会特征。Chen等（2006）认为董事会规模与企业财务业绩存在正相关的关系。于东智等（2004）也同样认为董事会规模影响公司业绩。胡奕明等（2008）、韩立岩等（2009）和江向才等（2006）指出独立董事比例、董事长和总经理是否合一对上市企业公司治理与财务业绩有显著影响。本文选择代表企业董事会特征的指标变量包括：董事会规模、独立董事比例、监事会规模、CEO两职状态等。

（3）股权结构。Shleifer等（1986）在早期的研究中发现，股权集中度越高的企业，股东通过公司治理机制影响经理层经营的能力越强，能有效减少经理人员的机会主义倾向。徐莉萍等（2006）的研究表明股权集中度越高企业业绩越好，但刘银国（2010）认为股权集中度与企业业绩存在反向变动的关系。

（4）市场指标。市场指标反映企业的流动性。钱苹等（2015）研究发现，股票换手率这一指标能够反映企业正常经营与否，并指出非正常企业的股票交易不如正常企业活跃。Wang等（2013）也指出，相对于其他反映企业经营情况的市场指标，股票换手率对企业业绩的反映更为灵敏。因此，在使用一般市场指标的前提下，本文加入股票换手率这一指标作为衡量企业信用风险的市场指标，具体指标见表3。

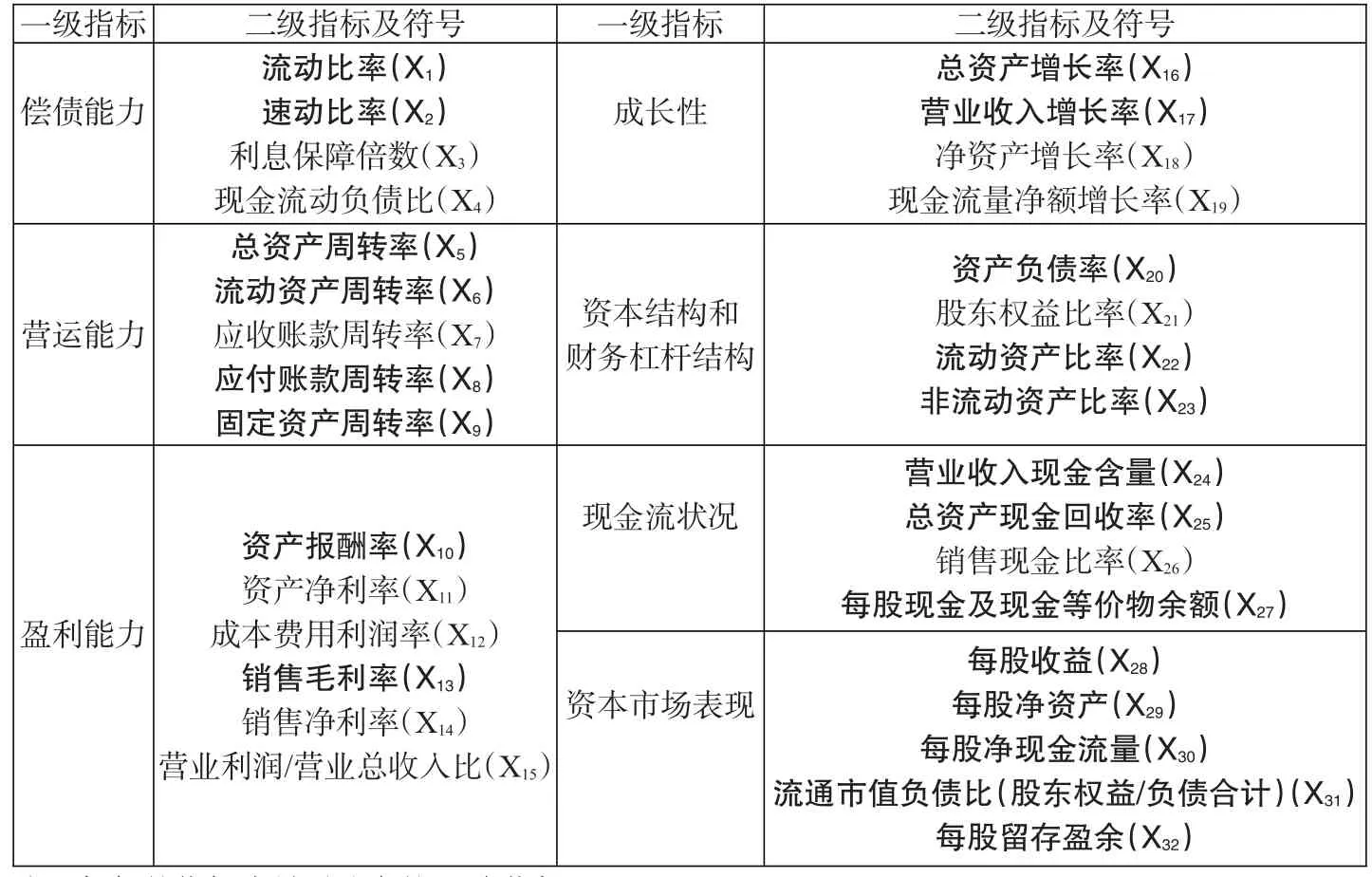
表2：财务业绩指标

为了选择最能够体现评估企业信用风险的指标，同时考虑到已列指标之间存在的多重共线性，本文选择逐步回归法筛选特征变量，设置进入模型以及被删除的概率分别为5%和10%，选出对企业信用风险影响显著的指标，构建评价中小企业信用风险状况的指标体系，结果见表4。

五、模型构建与检验

设置RBF为SVM的核函数，反复试验选择惩罚参数C为0.5，核函数中的g为5，KNN算法中K值为5。研究通过十折交叉验证选择使得模型性能最优的ODR参数β。本文编程部分通过matlab2012a实现，统计分析部分通过SPSS22.0实现。

（一）最优ODR-BADASYN-SVM模型的构建

在不平衡样本的分类中，对ODR中参数β的选择直接影响着模型的性能。我们采用十折交叉验证法描述参数β在区间[0，1]上的不同取值对于模型分类性能的影响（见图1）。

从图1中能够看出，在β=0处，模型中ODR未参与抽样，未删除正常企业样本，模型性能低。当β=0.1时，ODR算法对正常企业样本进行了欠采样，删除了正常企业中一定比例的噪声样本，再通过BADASYN算法对少数类样本进行合成，整个模型的性能较第一阶段有了较大提高。在此后的过程中，随着β数值的不断增大，ODR算法对多数类样本的删除比例也逐渐增加，模型G性能与F性能都比较平稳。当β=0.8时，模型G性能达到峰值，且F性能也处在较高水平。当β临近1时，模型的G性能较之前有所降低，F性能降低幅度明显。原因是ODR算法过多地删除了多数类样本，损失了部分有效信息，模型性能尤其是对少数类样本的分类性能降低。

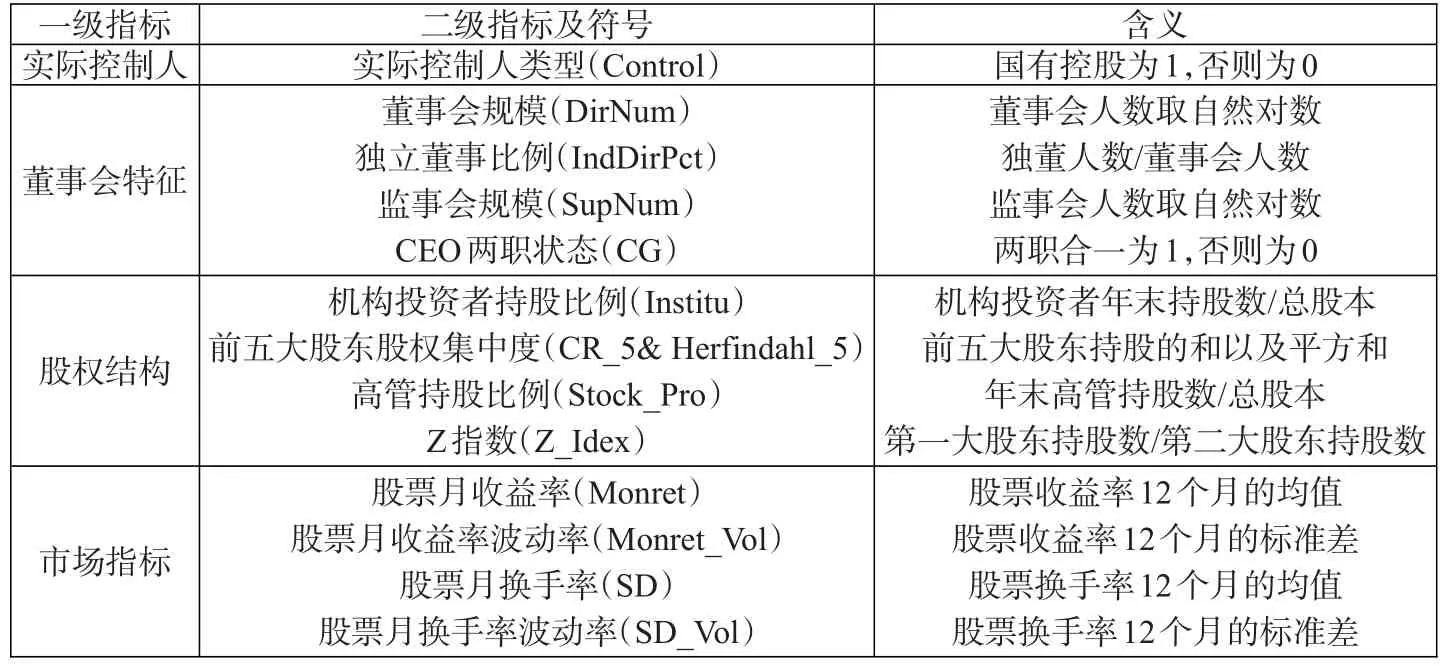
表3：非财务业绩指标

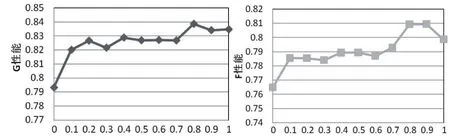
图1：不同β值对模型分类性能的影响

综合以上分析，本文认为当β=0.8时，ODR-BADASYN-SVM模型能够较为均衡地处理多数类噪声样本与边界少数类样本，模型性能达到最优。

（二）最优ODR-BADASYN-SVM模型与其他SVM模型的性能比对

在以上分析中，我们得出了能使ODR-BADASYNSVM模型性能最优的β系数。但该模型是否能够有效提升SVM模型，需进一步验证。为此，本文对最优ODR-BADASYN-SVM模型与SVM、ODR-SVM和BADASYN-SVM模型分类性能的差异进行了研究。

为比较不同模型性能，设置使ODR-BADASYNSVM模型性能最优的参数β值为0.8，ODR模型中的参数β值为1。其余模型参数与之前分析保持一致，同样采用十折交叉验证法，得出不同模型性能，结果见表5。

从表5可以看出，样本不平衡时SVM模型的分类性能最差，G性能和F性能均处在最低的水平，在运行过程中SVM模型将少数类违约企业样本错分为正常企业样本数量较多。由此，本文认为未做改进的SVM模型在不平衡样本数量下无法有效预测中小企业的信用风险。从表中还可以看出，最优ODR-BADASYN-SVM模型的G性能和F性能均高于ODRSVM和BADASYN-SVM模型，说明最优ODR-BADASYN-SVM在预测精准度上高于ODR-SVM和BADASYN-SVM模型。

为了使实证结果更具客观性，同时更为科学地说明以上四种模型对不平衡样本数量下对企业信用风险预测性能的差异，本文对各个模型预测结果进行了配对样本T检验，结果如表6。

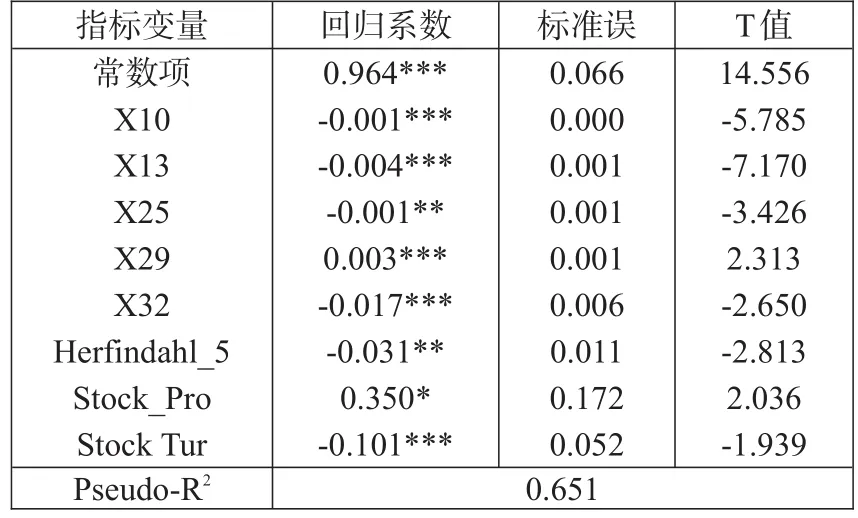
表4：指标回归结果

表5：模型性能对比

从表6可以看出，不做任何改进的SVM模型G性能和F性能与其他三个模型都是在1%的水平上存在显著性差异，能够看出在对不平衡数据的信用风险评价中，SVM模型的预测性能显著低于ODR-SVM、BADASYN-SVM和ODR-BADASYN-SVM模型，也由此肯定了与SVM相结合的ODR、BADASYN和ODR-BADASYN对SVM模型在不平衡数据分类中的改进作用。

从表6也可以看出，BADASYN-SVM模型性能与ODR-BADASYN-SVM模型的性能各在1%的水平上存在显著差异。在运算过程中，BADASYN算法重点在对于违约企业边界样本的合成，没有关注正常企业样本中信息含量少的噪声样本，模型在分类过程中对于两类企业的错分均比较多，致使BADASYN-SVM模型的G性能和F性能较低。这表明，在3.42：1的样本不均衡程度下仅将BADASYN与SVM模型相结合只对违约企业边界样本进行合成而不处理正常企业噪声样本的方法相对于其他两类方法对SVM模型性能的提升贡献能力有限。

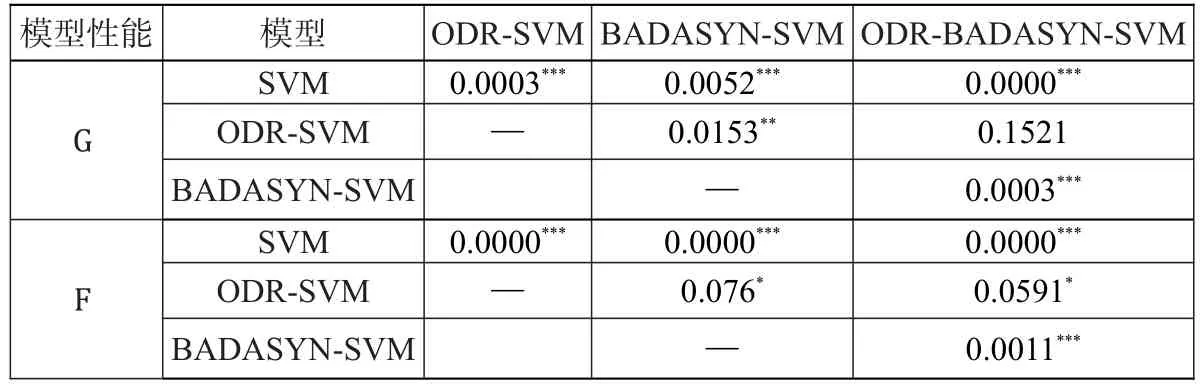
表6：模型性能差异对比

对比ODR-SVM和ODR-BADASYN-SVM模型性能的差异程度，两者F值在10%的水平上拒绝0假设，结合模型预测性能精度表可以看出，ODR-BADASYN-SVM模型的F性能显著优于ODR-SVM模型的F性能。原因是在分类过程中，相对于ODR算法关注点在对正常企业样本的删除上，ODR与BADASYN相结合的算法能够兼顾对正常企业样本中的噪声样本的删除以及少数类违约企业边界样本的合成。而且通过观察两个模型G性能的均值和标准差大小，能够看出ODR-BADASYN-SVM模型的G性能均值大于ODR-SVM的G性能，而且前者的标准差小于后者，说明前者的G性能较后者稳定。再结合ODR-BADASYN-SVM模型判断少数类违约企业的F性能显著优于ODR-SVM模型，本文认为ODR-BADASYNSVM模型在判断不平衡样本时对SVM模型的提升能力高于ODR-SVM模型。

由此能够看出，将ODR和BADASYN算法相结合的SVM模型，既能通过逐级优化递减的方法对多数类正常企业样本进行欠采样，又能对少数类违约企业的边界样本进行合成，能够克服SVM模型不适用与不平衡数据分类的问题，有效提升SVM模型的分类性能。

综合以上分析，在将ODR与BADASYN算法相结合的SVM模型中，对于ODR算法中参数β的选择对于模型性能影响较大。β=0.8时，ODR-BADASYN-SVM性能达到最优，该最优ODR-BADASYN-SVM信用风险评估模型在G性能与F性能上均显著优于不做任何改进的SVM模型和只处理违约企业样本的BADASYN-SVM模型。同时最优ODRBADASYN-SVM模型F性能显著高于ODR-SVM的F性能，G性能相对较高且分类性能稳定。可以看出，ODR与BADASYN算法相结合的SVM模型性能高于单独使用ODR或者BADASYN算法的性能，并且能够显著提高SVM模型在不平衡数据分类中的性能。因此，结合了ODR与BADASYN算法的SVM模型能够较为科学地预测中小企业信用风险存在与否，能够使外部投资者更好地了解中小企业信用状况，为更好开展中小企业质押融资提供依据。

六、结论与不足

本文选取2007—2015年我国A股非金融上市公司中的中小企业为研究对象，将财务失败与否作为判断企业存在信用风险与否的标准，构建了3.42：1的正常企业与违约企业的样本集。在文献法、调研法的基础上，通过统计检验和逐步回归法确定了评价企业信用风险的指标体系。在SVM中，引入ODR算法对正常企业样本中噪声样本进行删除，引入BADASYN算法合成违约企业边界样本，通过参数β的选择构建了最优ODR-BADASYN-SVM模型用以评价中小企业信用风险。研究结果表明，最优ODR-BADASYN-SVM模型的预测性能显著优于SVM和BADASYN-SVM模型，并且较ODR-SVM模型具有较高的F性能以及更为稳定的G性能，说明ODR-BADASYN结合的方法有效提高了SVM在不平衡数据中的分类性能，能够在中小企业信用风险评价过程中发挥作用。

本文通过构建ODR-BADASYN-SVM模型对中小企业信用风险进行评估，能够帮助银行等外部投资者了解企业实际信用状况，降低信息不对称性以及由此造成的损失，从而为更好开展对于中小企业的贷款业务提供数据支撑。然而，本文所构建的信用风险评估结果仅能呈现一种二分的预测，即只能判断出企业是正常企业或者违约企业，却不能对于企业存在的信用风险的大小程度给出度量。因此，如何改进所构建的不平衡样本分类算法，以获得中小企业信用风险程度的测量，还有待于进一步研究。

[1]Stiglitz J E，Weiss A.1981.Credit Rationing in Markets with Imperfect Information[J].The American Economic Review，71（3）.

[2]Beaver W H.1966.Financial ratios as predictors of failure[J].Journal of Accounting Research，4（1）.

[3]Altman E I.Financial Rations，Financial Ratios，Discriminant Analysis and the Prediction of Corporate Bankruptcy.The Journal of Finance，23（4）.

[4]Ohlson J A.1981.Financial Ratios and the Probabi-listic Prediction of Bankruptcy[J].Journal of Accounting Research，18（1）.

[5]Aguilera A M，Escabias M，Valderrama M J.2006.Using principal components for estimating logistic regression with high-dimensional multicollinear data[J].Computational Statistics&Data Analysis，50（8）.

[6]Dong G，Lai K K，Yen J.2010.Credit scorecard based on logistic regression with random coefficients[J].Procedia Computer Science，1（1）.

[7]Cortes C，Vapnik V.1995.Support-vector networks[J].Machine Learning，20（3）.

[8]Vapnik V N.1995.The nature of statistical learning theory[M].NewYork：Springer.

[9]Gong M G，Du H F，Jiao L C.2006.Optimal approximation of linear systems by artificial immune response[J].Science in China，49（1）.

[10]Chawla N V，Bowyer K W，Hall L O，et al.2002.SMOTE：synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research，16（1）.

[11]Gunn S R.1998.Support vector machines for classification and regression[J].ISIS technical report，14.

[12]Friedman E，Johnson S，Mitton T.2003.Propping and tunneling[J].Nber Working Papers，31（4）.

[13]中国的选择：抓住5万亿美元的生产力机遇[R].麦肯锡全球研究院，2016，6.

[14]赵岳，谭之博.电子商务、银行信贷与中小企业融资——一个基于信息经济学的理论模型[J].经济研究，2012，（7）.

[15]郭娜.政府?市场?谁更有效——中小企业融资难解决机制有效性研究[J].金融研究，2013，（3）.

[16]张目，周宗放.基于多目标规划和支持向量机的企业信用评估模型[J].中国软科学，2009，（4）.

[17]丁欣.国外信用风险评估方法的发展现状[J].湖南大学学报社会科学版，2002，（s1）.