力学中自锁现象的应用实例分析

李建军

自锁现象是力学中的一种特有现象，当自锁条件满足时，无论施以多大的力都不可能让一个物体与另一个物体之间发生相对运动。本节通过实例谈谈这种现象在生产和生活中的应用。

例1 1999年，中国首次北极科学考察队乘坐我国自行研制的“雪龙”号科学考察船对北极地区海域进行了全方位的卓有成效的科学考察。这次考察获得了圆满的成功，并取得一大批极为珍贵的资料。“雪龙”号科学考察船不仅采用特殊的材料，而且船体的结构也满足一定的条件，以对付北极地区的冰块和冰层。它是靠自身的重力压碎周围的冰块，同时又将碎冰挤向船底。如果碎冰块仍挤在冰层与船体之间，船体由于受巨大的侧压力，而可能解体，如图1所示。为此，船壁与竖直平面之间必须有一个恰当的倾斜角θ，设船壁与冰块间的动摩擦因数为μ，试问为使压碎的冰块能被挤向船底，θ角应满足什么条件。

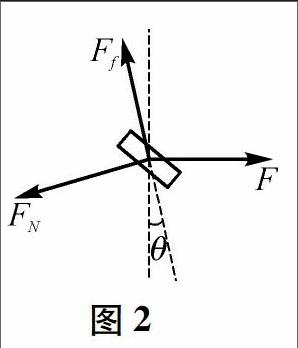
解析 首先让我们来定性分析这个问题。压碎以后的冰块怎样才能够挤向船底呢？必须使冰块所受合力沿船体壁向下（即指向船底）。选取碎冰块作为研究对象，其所受作用力分别为：船体对它的垂直于船壁向外的弹力F_N，冰层对它的水平方向的挤压力F，船壁与碎冰块之间的摩擦力F_f，要使冰块向船底运动，摩擦力的方向必沿船壁向上。此外，碎冰块还受到自身重力与水对它的浮力作用，由于这两个力的合力与前面分析的三个力相比很小，为研究问题方便，可忽略不计，这是中学物理常用的一种理想化思维方法，故冰块的受力如图2所示。从碎冰块的受力图可见，F沿船壁向下的分力越大，摩擦力F_f越小，碎冰块就越容易被挤向船底。实际上，如果假设冰层对冰块的挤压力F是一个定值，则F沿船壁向下的分力越大，摩擦力F_f也一定越小。而θ角越大，F沿船壁向下的分力亦越大，故θ角一定要大于某一临界值，才能够使压碎的冰块被挤向船底。

设碎冰块恰能被挤向船底，将冰块所受的力分解到沿船壁方向与垂直于船壁方向，由物体的平衡条件，得

Fcosθ-F_N=0

Fsinθ-F_f=0

又F_f=μF_n

即得tanθ=μ

故θ角必須满足

θ>arctanμ。

例2 螺丝钉

螺丝钉是机械中不可缺少的零件，如图3所示。当用它紧固机器零件时，会在螺杆、螺帽间产生巨大的压力，螺帽尽管受到很大的压力，仍然不会移动，试分析其原理。 解析 螺丝钉是利用斜面自锁原理制成的。螺帽受压不会移动，则螺杆半径与螺距之间必须满足一定的关系。螺杆的外表面展开是一个斜面，如图4所示。设螺杆、螺帽间动摩擦因数为μ，螺杆半径为r，斜面的高为螺距h，底为圆周长2πr，其倾角的正切值tanθ=h/2πr。根据斜面自锁条件μ≥tanθ得μ≥h/2πr，则h≤2πημ。

例3 自锁起重吊钩

如图5（a）所示，由两根短杆组成的一个自领起重吊构，将它放入被吊的空罐内，使其张开一定的夹角压紧在罐壁上，其内部结构如图5（b）所示。当钢绳勾速向上提起时，两杆对罐壁越压越紧，若摩擦力足够大，就能将重物提升起来，罐越重，短杆提供的压力足够大，称为“自锁定机构”，若罐重力为G，短杆与整直方向夹角为θ=60°，求吊起该重物时，短杆对罐壁的压力（短杆的质量不计）。

解析 如图6所示，对0点受力分析。两根短杆沿杆的弹力F的合力与钢绳的拉力T（T=G）等大反向，故

2Fcosθ=G

如图7所示，短杆对罐壁的作用力又可以分解为对壁的压力F_N和竖直向上的静摩擦力F_f，则

F_N=Fsinθ=√3/2G.

这是一个借助巧妙的机械装置达到自锁的模型。由分析可见，当自锁机构的两边与罐接触后，产生弹力和摩擦力托起罐，如果不发生相对滑动，θ有增大的趋势，θ越大，F_N就越大，即所谓越挤越紧，因而可提供的最大静摩擦力就越大，重物更不容易滑脱。这种机械装置自锁的应用在日常生活中是比较普遍的。

例4 门锁的自锁现象一般教室门上都安装一种暗锁，如图8

本题通过控制摩擦因数μ达到的自锁，故要消除自锁，一方面可以减少摩擦，即在锁舌的表面涂润滑油或滑石粉。另一方面可将锁舌与锁槽接触的那一面用钢锉锉掉一些，使锁舌顶角θ增大一些，则N在使弹簧压缩方向上产生的效果大一些，都可以消除自锁现象。endprint