例谈“机械能守恒定律”的复习方法

吴含章

复习不仅仅是简单的“温故”，也不能把一章的知识面面倶到地再重新学习一遍，而是要根据一章知识的掌握情况有所侧重，针对性地进行复习以达成目标，笔者倾向于采用“以问题为中心”的方法和一题多解进行复习。

—、以问题为中心

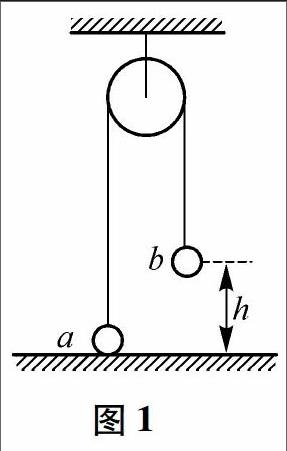
问题情境1：如图1，一根长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球a和b，a球质量为m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧，从静止开始释放b，a可能达到的最大高度为多大？

有一位学生是这样解的：取a、b两球为系统，b球减小的重力势能等于两球增加的动能和a球增加的重力势能。

列出表达式：

针对这类典型错误，我们不妨分层设问，在文中探求答案：

问题1：b从释放到着地，重力对b所做的功多大？

解析 ：

问题2：b着地瞬间的速度大小？

解析 ：a、b两球为系统机械能守恒：

问题3：a球可能达到的最大高度为多大？

解析 ：

相对于地面a可能达到的最大高度H=h+ha=1.5h

【点评】这类问题有不少学生仍习惯用牛顿运动定律来求解。機械能守恒定律这章先从能量的概念认识到根据牛顿运动规律推导出动能定理；再由动能定理推导出机械能守恒定律；再由功能关系总结得出能量守恒定律。所体现的物理思想是培养学生能够以能量为一条主线贯穿学习整章内容，因此，在解决此题时，我们不能只满足于解出来，而要注意培养从能量角度去认识问题、分析问题、解决物理问题的科学思维。 问题4：从静止开始释放b到a上升至最大高度，a球机械能如何变化？b球机械能如何变化？a、b系统的机械能是否守恒？

解析 ：a球机械能先增加后不变，b球机械能先减小后着地瞬间损失为零，a、b系统的机械能先守恒后减小。 【点评】通过以上分层设问，既囊括了做功、动能定理、机械能守恒定律的条件和应用等知识点，又浅入深出地理解了这类问题。

二、一题多解，重构知识体系

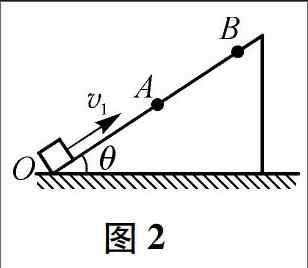
问题情境2：如图2，一木箱从倾角为θ的固定斜面底端依靠惯性以速率ν₁向上运动，回到出发点时，它的速率为ν₂，且ν₂<ν₁，假设木箱由斜面底端回到出发点的中点为A，且斜面底端的重力势能为零。则向上运动的过程中，动能和势能相等点位置应在中点A的上方还是下方？

解法1：常规的定量分析法

如图2所示，假设木箱质量为m，其运动过程中的摩擦力为f，由最低点O向上运动到达最高点B的最大距离为L，两者的中点为A，木箱由最低点向上运动到最高点，依功能关系可知：

依题意，地面势能为零，设动能和势能相等点的位置在D，则：

其中L_D为O、D两点间的距离，ν_D是通过D点的速度，从O到D点由功能关系得：

联立以上三式可得

所以由以上定量分析可见，木箱向上运动的过程中，动能和势能相等点的位置应在中点A的上方某处。 解法2：图象分析法

由功能关系，木箱在离开出发点O向上运动的过程中，上滑位移x时的动能为，重力势能为 。显然两种机械能随x线性变化。因为有摩擦力，所以上滑至最远点B的机械能较初始点O点的机械能小，即 。在同一坐标系中作出Ek、Ep随x的变化图象a和b，如图3所示。由图可得当木箱运动至x=L/2处有E_Pk；，因此，木箱向上运动的过程中，动能和势能相等点的位置必在中点A的上方。

解法3：特殊位置法

当木箱上滑至中点A时，有E_Pt=1/2E_Pb。假设木箱在A点有E_ka=E_Pt，则木箱此处的动能仅可以满足从A到B重力势能的增加量，而没有多余的动能来克服滑动摩擦力做功，故假设不成立。因此，木箱在A点应该余下更多的动能才能满足AB段运动的需要，即在A点满足E_ka>E_Pt，所以木箱只有到达A点上方的某处时才会出现动能等于势能的情况。

【点评】从本题的三种解题方法可以看出，机械能问题的处理方法很多，视角不同，往往会有不同的效果，图象分析法形象直观易懂，有时可带来别具洞天的解题功效。

复习的作用，不仅仅是为了巩固知识，还应有积极的推进作用，温故而知新，我们在复习中要注重学习过程中知识网络的构建，对于典型题目通过问题解决重构知识体系、探索其多种解法、构建知识框架以开阔思路、发展思维能力和综合分析问题能力，同时注意知识的灵活运用，真正提高物理学习的素养和能力。