求解直线问题有窍门
2018-03-06熊杰
熊杰

直线是解析几何所研究的基本对象之一,我们就以与直线相关的问题为例,谈谈解题中的注意点及方法选择,助你掌握此类问题的解题窍门.
一、选哪种形式好
直线方程有五种形式,各有各的特点,在使用的时候要根据条件合理选择,同时还不能忽略各种形式的适用范围.
例1 求过点A(1,2)且在两坐标轴上截距相等的直线.
错解 由直线在两坐标轴上截距相等,設直线方程为想x/a+y/a=1,代人点A(l,2),得a=3,直线方程为y=-x+3.
此处使用截距式看似简单直接,其实隐含了一个不能忽略的要点,即直线方程的截距式在使用时是有限制的,它所表示的直线不能垂直于坐标轴,也不能过原点.因此本题在求解时应该对这两种情况进行单独讨论.
解答补充 当截距为0时,直线过原点,满足题意,直线方程为y=2x,
所以直线方程为y=2x或y=-x+3.
当然本题还可以用另一类直线方程求解,因为所求直线上一点已经明确,因此为了减少未知参数,我们可以采用点斜式来求解.但在使用点斜式时要注意是否有直线斜率不存在的特殊情况.
另解 由题意,直线斜率存在,设直线方程为y-2=k(x-1),
当x=0时,y=2-k,当y=0时,x=1-2/k
2-k=1-2/k,解得k=2或-1
所以直线方程为V=2r或y=-x+3.
此两种方法均为代数法解答,即为设直线方程并求参数的基本方法,区别仅在于运用了不同形式的直线方程进行运算,两种方法各有特点,同学们要仔细体会,当然,如果你看出了本题的几何背景,那么也可以用几何解法求解,
变式 已知直线l过(0,1),且点A(-3,-4),B(6,3)到直线l的距离相等,求直线l的方程.
鉴于几何图形的直观特点,本题很多同学想要用几何的方法来解题,但同时也出现了很多问题.
几何解法分析:
如图1,本题的直线l存在两种情况,它既可以是一条平行于AB的直线,也可以是一条过AB中点的直线,在分析过程中,有一些同学出现了漏解的情况,有的只注意到平行于AB的直线,有的只想到过AB中点的直线,思考不全面让他们失分.而直接用代数的方法求解则可避免这种失误,也就是说解析法可能更加适合这类问题.二、不能忽略图形
例2 已知直线z经过直线l1:2x+y5=0与l2:x-2y=O的交点.
(1)若点A(5,O)到l的距离为3,求l的方程;
(2)求点A(5,O)到l的距离的最大值.
), 解 (1)由2x+y-5=0,x-2y=0解得交点P(2,1),
当直线斜率k不存在时,直线l:x=2,此时l到点A距离为3;
当直线斜率k存在时,设直线方程y
(2)由交点P(2,1),如图2,过P作任一直线l,设d为点A到l的距离,则d≤PA(当l⊥PA时等号成立).
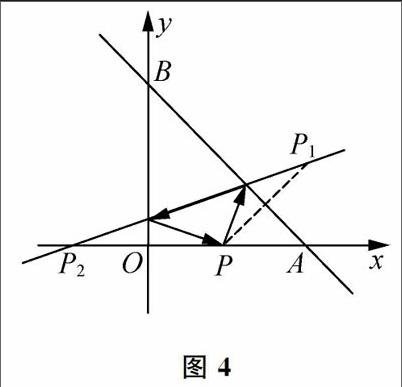
例3 如图3所示,已知两点A(4,o),B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,求光线所经过的路程.
本题若想分别计算三段光线的长度显然是不合理的,由光学作图中的对称性原理可知做出如下的图形即可很便利地求解光线所经过的路程,
常见的作图有如下两种情况,
如图4所示,做P关于直线AB的对称点P1,再做p关于y轴的对称点P2,P1P2长度即为所求路程.
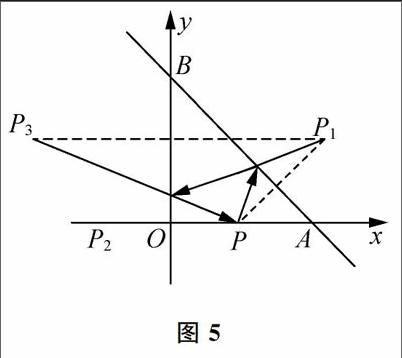
如图5所示,做P关于直线AB的对称点P1,再做P1关于y轴的对称点P3。,P3P长度即为所求路程.
两种作图方法均利用了图形对称性的原理将原本不在一条直线上的三段路程转化到一条直线上求解,
后续的问题就只要求出相应的对称点坐标即可,首先我们利用线段P1P被直线AB垂直平分的特点,先求出P1的坐标.
解 设P1(x0,y0),lAB:y=-x+4,
由直线AB垂直且平分线段PP1,得y0/x0-2)×(-1)=-1 y0/2=-(2+y0)/2+4解得P.(4,2),关于y轴的对称点很特殊,很快可得P2(-2,0),P。(-4,2).
除了点的对称问题我们还会碰到直线的对称问题,其实只要关注直线上的一些特殊点,这种对称问题的本质也可以转化到点的对称上来求解.
笛卡儿曾经说过:“我想寻求一种新的,包含两门学科的好处,而义没有它们缺点的方法.”解析几何包含了两门学科的优点,我们所要做的就是找出这些优点,让它们为我所用.endprint
