水平与微倾斜管内气液两相流长气泡形状实验和模型研究
2018-03-06吴志成熊珍琴顾汉洋
吴志成, 熊珍琴, 顾汉洋
(上海交通大学 核科学与工程学院, 上海 200240)
符号说明:
L——气泡长度,m
D——管道内径,m
θ——管道倾角,(°)
USL——液体流速,m/s
αl——液相相含率
αg——气相相含率
h2——水跃面中点x2处液膜厚度,m
h3——水跃面中点x3处液膜厚度,m
hl——液膜高度,m
τl——液相与壁面间剪切应力,N/m2
τg——气相与壁面间剪切应力,N/m2
τi——气液两相间剪切应力,N/m2
Sl——液相表面湿周, m
Sg——气相表面湿周,m
Si——气液两相相界面表面湿周,m
fl0——摩擦因子
Rel——液相雷诺数
Hl——液膜厚度无量纲数
pl——液相平均压力,Pa
pg——气相平均压力,Pa
b——截面宽度,m
A——横截面积,m2
ρl——液相密度,kg/m3
ρg——气相密度,kg/m3
αx1——点x1处液相相含率
ul——相对Vb下的液相瞬时平均速度,m/s
ug——相对Vb下的气相瞬时平均速度,m/s
ξ——气弹区长度无量纲数
Vb——气弹移动速度,m/s
Fp,x2——点x2处由重力引起的水压,N
Fp,x3——点x3处由重力引起的水压,N
Fw——水跃面中液相与管壁面的阻力,N
Ux2——水跃面中点x2处的平均液相速度,m/s
Ux3——水跃面中点x3处的平均液相速度,m/s
pin——水跃面中点x2处平均液相速度与气弹移动速度差引起的水压,N
pout——水跃面中点x3处平均液相速度与气弹移动速度差引起的水压,N
段塞流是工业领域包括石油工业和核工业领域十分常见的流型.由于其随机性和间歇性,因此结构十分复杂,其中气弹是形成段塞流复杂结构的主要原因.最早Dukler等[1]提出了等效段塞单元的概念,其将气弹假设为等长度的气弹,在其模型中假设气弹充分发展,液膜厚度不随气弹体长度变化.而后大量的理论模型都采用这种假设(Nicholson等[2],Kokal等[3],Taitel等[4]).然而大量的水平管和倾斜管中的实验结果表明,气弹区中任一横截面的液膜厚度均随着距离气弹区头部的长度变化而发生变化.Mazza 等[5]对液膜模型进行了分析,发现假定液膜高度一致的段塞流模型将会导致气弹区含气率的预测值偏高.
在水平管和倾斜管中,受重力影响,位于管道上半部分的长气弹区和下半部分的液膜之间存在一个明显的交界面,因而形成各种形态的长气泡结构.不同的研究者采用电导或者电容的方法对其结构进行了测量(Roitberg等[6],Barnea等[7]).
Netto等[8]用位于水平管中部的电容探针测出掠过探针的长气弹体的气液交界面,得到了单气泡的形态特征,同时结合实验结果将气弹区分为气弹头、气弹体、气弹水跃面和气弹体尾部4个区域,分别建立了气弹形状的计算模型.但该模型仅能对水平管中的气液段塞流中的长气泡进行计算.
笔者针对不同内径的水平管和倾斜管内气液段塞流中长气泡的形态进行了实验研究,获得了不同参数(如气泡长度、液体流速、管径和管道倾角)对气泡形状的影响.同时,基于Netto等[8]的理论模型提出了一个适合水平管和倾斜管道内气弹形状预测的模型,并将该模型的预测结果与实验结果进行了对比验证.
1 实验系统及测量方法
Grenier[9]和Woods等[10]的实验结果表明,段塞流气弹区的形态只取决于气液混合速度,而与气液各相速度无关.为了消除气液连续流动在实验管道出口液量的间隙性引入的间隙性压力扰动以及便于控制气弹的长度,笔者在连续液相流动中注入单气泡进行实验,获得段塞流气弹区长气泡的形状.此时,气液混合速度等于液体流速.
单气泡实验系统如图1所示,实验系统由气水输送、液体计量、仪表测量和数据采集处理等部分组成,实验介质为空气-水.水经离心泵加压后由电磁流量计计量,进入管长为14.0 m,内径分别为D=0.025 m和D=0.05 m的透明有机玻璃管段内形成稳定的液相连续流,然后回到开口水箱.空气经过螺杆压缩机压缩后进入储气罐,通过开启和关闭三通管上游的闸阀V以及通过控制开启和关闭阀门之间的时间控制,向实验管道的连续液相流注入单气泡,并控制气泡的长度.为了尽量减少气泡注入时对液相连续流的扰动,同时保证气体速度近似为0,将储气罐的压力控制在比实验管道段入口压力p2高30 000~40 000 Pa的范围.实验的液体流速为0.20~1.82 m/s,气泡长度为0.26~10.9 m,实验管段倾角为水平和下倾1°.有机玻璃管段内沿流动方向布置了3组双平行探针,以测量单气泡的气液相界面,分别位于实验段入口 10.0 m、 11.8 m和12.0 m处(图1中W1、W2和W3处).每组双平行探针由直径为0.15 mm的不锈钢丝制成,间距为2.0 mm,如图2所示.实验前对每组探针进行了细致的标定,由于单气泡掠过探针之前和之后探针的输出信号为满管水的电导率值,实验中将各自得到的满管水的电导率作为参考值,对探针标定曲线进行无量纲化,以消除实验过程中水温变化对探针输出信号的影响.

图1 实验系统原理图

图3给出了液体流速为0.30 m/s时W2和W3处探针得到的气泡形状.两气泡界面重合良好,说明在实验范围内W2和W3处得到的气泡形状已经充分发展.

图3 低流速下W2、W3处得到的气泡形状
Fig.3 Shapes of bubbles obtained at pointsW2andW3under low velocity conditions
2 实验结果与分析
实验结果表明,长气泡的形状受气泡的长度、液体流速、管道倾角以及管径的影响.图4(a)给出了在相同的液体流速条件下,不同气泡长度的气泡形状.由图4(a)可知,气泡长度对气泡的头部以及气泡体并无影响,但在低流量下对气泡尾部的影响却十分显著.随着气泡长度的增加,阶梯状尾部结构的水跃面逐渐升高,而气泡尾的长度迅速缩短,最终气泡尾部消失,而只出现水跃面.
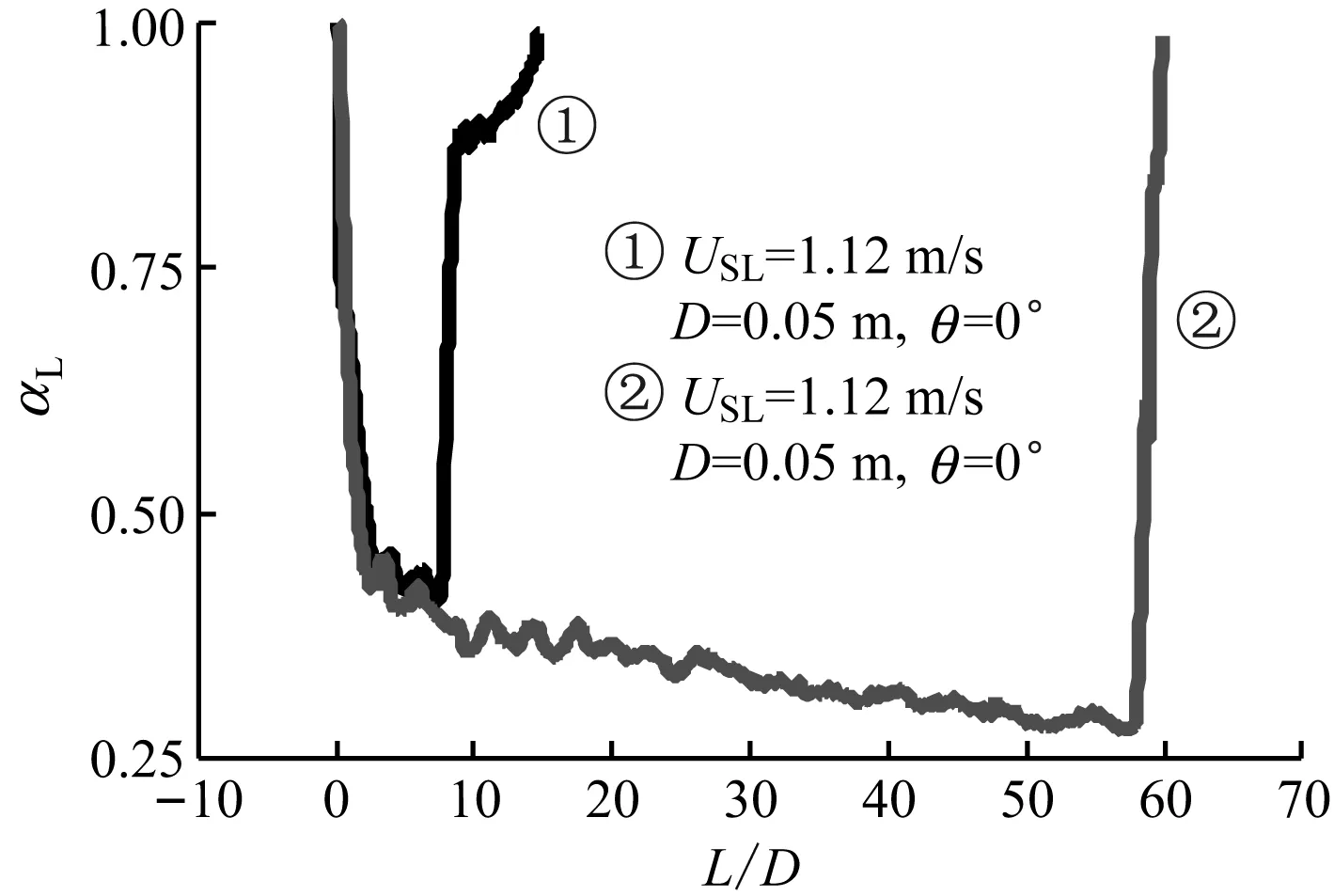
(a) 不同气泡长度下气泡界面特征

(b) 不同液体流速下气泡界面特征
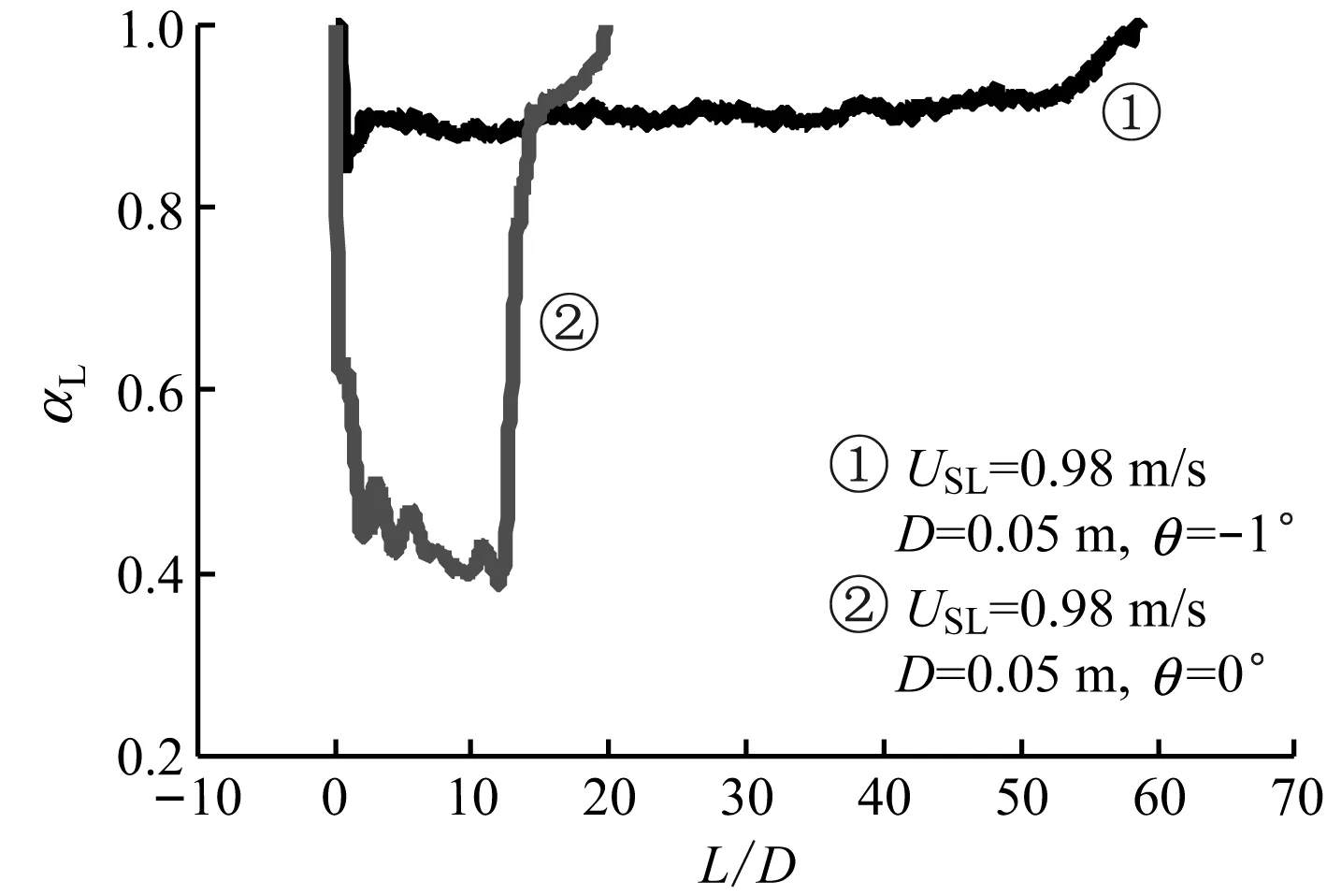
(c) 不同管道倾角下气泡界面特征

(d) 不同管径下气泡界面特征
气泡形状随液体流速的变化如图4(b)所示,在水平管气液段塞流中,当液体流速较小时,气液两相交界面上存在十分规则的二维界面波,其波幅沿着气泡长度方向逐渐衰减,气泡尾部呈阶梯状结构.随着液体流速逐渐增大,气液界面上的界面波逐渐消失,界面变得光滑,而水跃面升高,气泡尾缩短,最后消失,水跃面直接到达上壁面.
图4(c) 给出了在相同液体流速条件下管道倾角对气泡形状的影响.由图4(c)可知,下倾角1°管内气泡与水平管内气泡相比,气液界面明显升高,气泡尾部明显拉长.
图4(d)给出了不同管径对气泡形状特征的影响.由图4(d)可知,在相同液体流速条件下小管径内的长气泡气液界面更低,但气泡尾部的水跃现象更剧烈.
3 气弹区界面结构数理模型
根据气弹区相界面结构特征,将气弹区分为气弹头、气弹体、气弹水跃面和气弹尾,如图5所示,并根据每部分的界面结构特征分别进行模化,建立适用任意倾斜角的管内气液段塞流气弹区相界面结构的一维数学模型.

图5 气弹区界面结构示意图
对于气弹头,采用与Fragunde等模型相同的方法,即采用Benjamin的势流方程,其解用二次多项式来近似:
αl=1.0-0.775(L/D)+0.345(L/D)2
(1)
用式(1)来描述气弹头部形状.对于气弹体,Cook等[11]提出了一维全耦合的水动力模型,并利用实验数据进行了验证,该模型的示意图如图6所示.使用Cook等的模型来计算气弹体的形状,气弹体液膜高度随气弹长度方向的变化由式(2)计算得到:
(2)
气弹体的液膜高度与液相相含率的关系由几何关系通过式(3)计算得到:

(3)
(4)
气弹区水跃面模型示意图如图7所示,假设控制容积x2-x3区域的气相压力为常数,液相的流动为一维,并且气弹水跃面内的液体不含弥散小气泡,对x2-x3区域的液相建立动量守恒方程:

(a) 气弹体示意图(纵剖面)
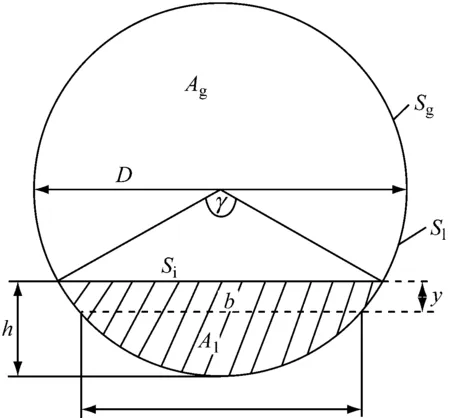
(b) 气弹体示意图(横剖面)
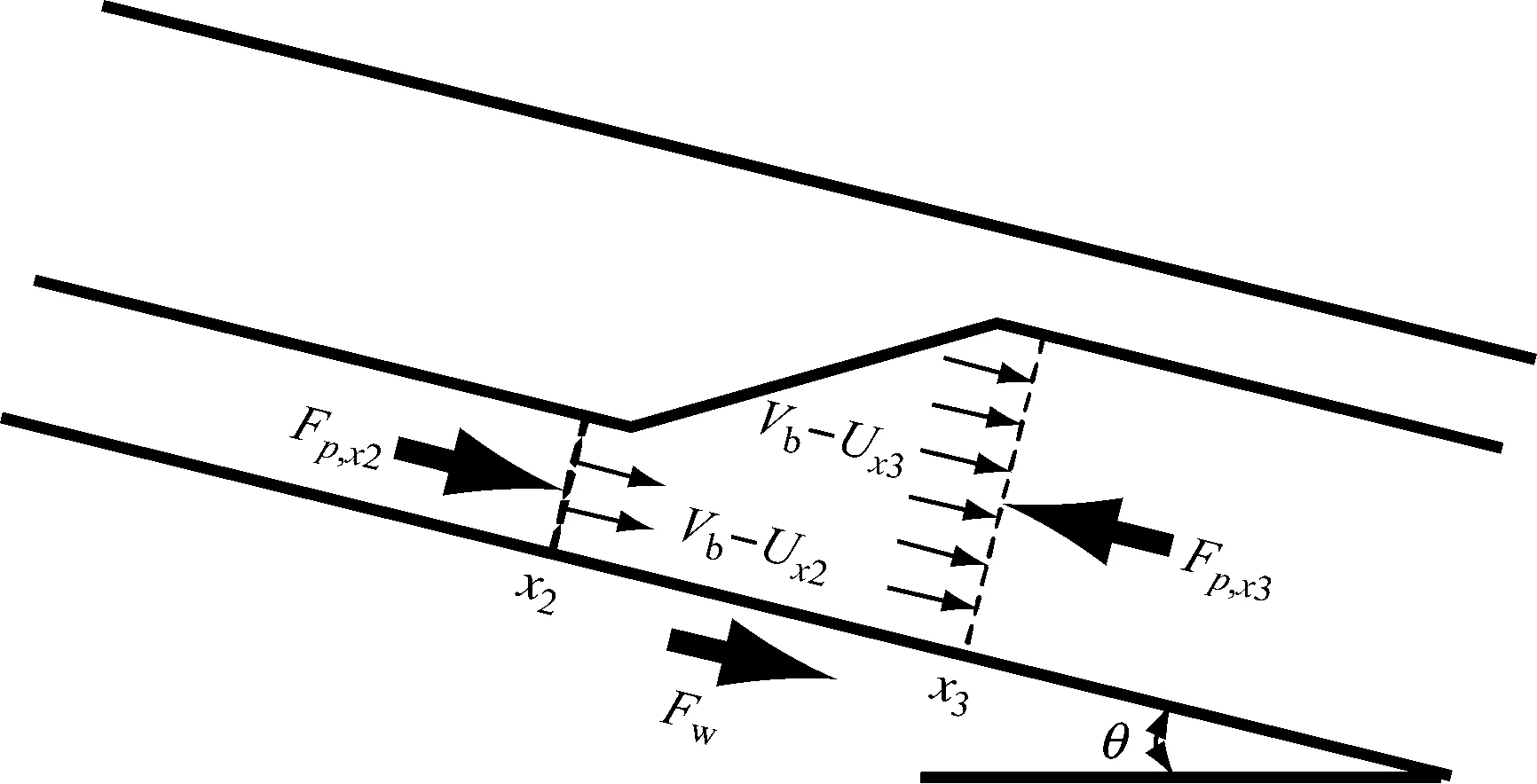
图7 水跃面区示意图
pout-pin=Fp,x2-Fp,x3+Fw
(5)
代入具体表达式得:

(6)
x2,x3点之间的壁面给液体的阻力Fw由式(7)计算:
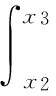
(7)
气弹尾部模型借鉴Fragunde (1999) 等模型,同时考虑管道倾斜的情况,获得气泡尾部的计算式:
(8)
采用Blasius关系式计算fl0,即:
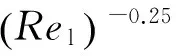
(9)
4 模型预测结果与实验结果的对比
计算时以实验中得到的气弹长度和气弹移动速度作为已知条件来确定气弹界面结构.图8给出了D=0.025 m和D=0.05 m 2种内径的水平管道内不同液体流速条件下不同气弹长度的气弹界面结构的模型预测结果(实线)和实验结果(虚线).由于所建立的一维模型是基于准稳态假设的,不能模拟气弹体气液界面上的界面波动特征,但由模型计算得到的气弹界面结构的轮廓与实验结果能很好地吻合.当液体流速较低时,气泡头部液位下降十分迅速、气泡头部影响区较小,距气泡头较近的水跃面的水跃现象较弱,气泡尾部长度较大,如图8(a)所示.随着气泡长度的增大,气泡尾部越来越短,直至消失,如图8(b)所示.当液体流速较大时,气泡头部影响区增大,气泡体液位下降增快,水跃现象加强,气泡贴近壁面的长尾消失,如图8(c)所示.当气泡长度相同,气泡尾部长度随着液体流速的增大而逐渐减小,最后消失,如图8(c)所示.在相同流速条件下,小管径下气泡水跃面现象更为显著,更不易形成长气泡尾,如图8(d)所示.当液体流速相同时,下倾角1°管内气泡较水平管内气泡液位下降减慢,水跃现象减弱,更容易形成长气泡尾,如图8(e)所示.下倾角过大时,气泡将呈现头尾倒置状态,而计算模型无法得到该状态下的界面结构轮廓.

(a) 低液体流速下不同长度下气泡形状

(b) 高液体流速下不同长度下气泡形状

(c) 不同液体流速下气泡形状
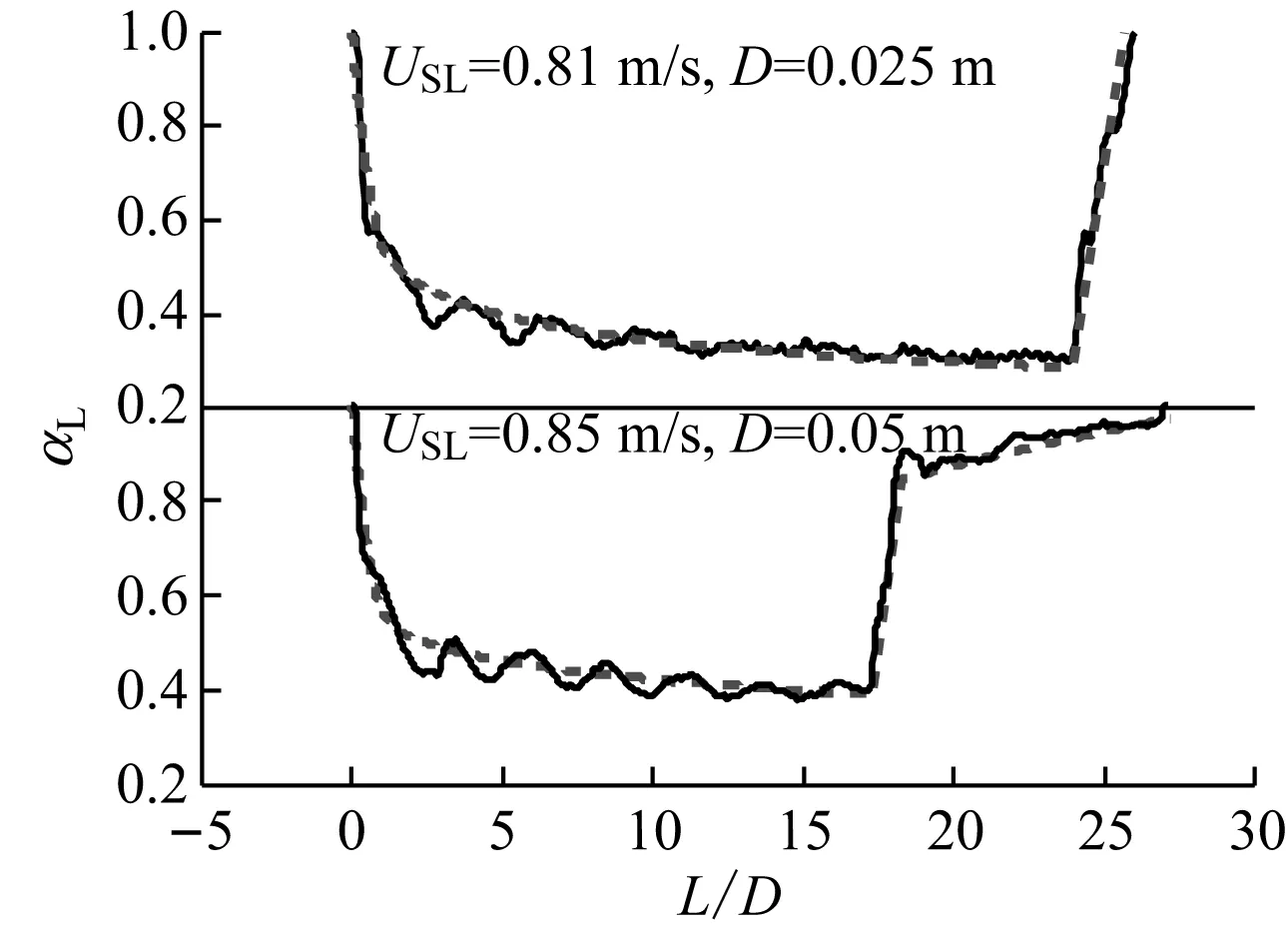
(d) 不同管径下气泡形状
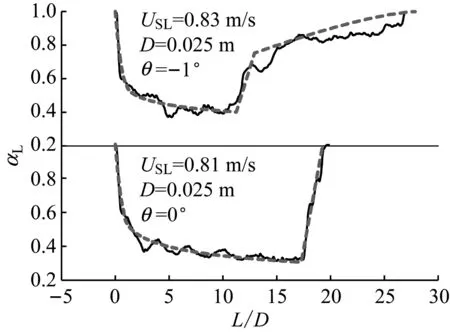
(e) 不同倾角下气泡形状
5 结 论
(1) 当流速较低时,气泡呈阶梯状,气泡形状具有气泡头部、气泡体、水跃面和气泡尾4部分;随着气泡长度的增大,水跃现象增强,气泡尾部缩短,直到消失;随着液体流速的增大,气液界面降低,水跃现象增强,气泡尾部更不易形成;下倾管道会削弱水跃现象,更易形成长气泡尾部;小管径下气泡水跃面现象较大管径下更强.
(2) 基于气弹区界面结构特征将气弹区分为气弹头、气弹体、气弹水跃面和气弹尾4部分,并分别建立一维计算模型.该模型的预测结果与实验结果能很好地吻合.
[1] DUKLER A E, HUBBARD M G. A model for gas-liquid slug flow in horizontal and near horizontal tubes[J].Industrial&EngineeringChemistryFundamentals, 1975, 14(4): 337-347.
[2] NICHOLSON M K, AZIZ K, GREGORY G A. Intermittent two phase flow in horizontal pipes: predictive models[J].TheCanadianJournalofChemicalEngineering, 1978, 56(6): 653-663.
[3] KOKAL S L, STANISLAV J F. An experimental study of two-phase flow in slightly inclined pipes—II.liquid holdup and pressure drop[J].ChemicalEngineeringScience, 1989, 44(3): 681-693.
[4] TAITEL Y, BARNEA D. Two-phase slug flow[J].AdvancesinHeatTransfer, 1990, 20: 83-132.
[5] MAZZA R A, ROSA E S, YOSHIZAWA C J. Analyses of liquid film models applied to horizontal and near horizontal gas-liquid slug flows[J].ChemicalEngineeringScience, 2010, 65(12): 3876-3892.
[6] ROITBERG E, SHEMER L, BARNEA D. Hydrodynamic characteristics of gas-liquid slug flow in a downward inclined pipe[J].ChemicalEngineeringScience, 2008, 63(14): 3605-3613.
[7] BARNEA D, ROITBERG E, SHEMER L. Spatial distribution of void fraction in the liquid slug in the whole range of pipe inclinations[J].InternationalJournalofMultiphaseFlow, 2013, 52: 92-101.
[8] NETTO J R F, FABRE J, PERESSON L. Shape of long bubbles in horizontal slug flow[J].InternationalJournalofMultiphaseFlow, 1999, 25(6/7): 1129-1160.
[9] GRENIER P. Evolution des longueurs de bouchonsenécoulement intermittent horizontal[D].France: Institut de Mécanique des Fluides de Toulouse,1997.
[10] WOODS B D, HANRATTY T J. Relation of slug stability to shedding rate[J].InternationalJournalofMultiphaseFlow, 1996, 22(5): 809-828.
[11] COOK M, BEHNIA M.Film profiles behind liquid slugs in gas-liquid pipe flow[J].AIChEJournal, 1997, 43(9): 2180-2186.
