跨音速透平叶栅尾缘劈缝射流的数值研究
2018-03-06姚世传轩笠铭施鎏鎏
姚世传, 陈 榴, 轩笠铭, 施鎏鎏, 戴 韧
(上海理工大学 能源与动力工程学院, 上海 200093)
透平高压级在考虑冷气掺混影响条件下的气动性能是提高发动机性能的关键.由于高温、高压、高负荷的特点,跨音速高压透平的试验非常困难,准备周期长,投入也相当大.Denton[1]指出,将先进的数值模拟方法应用于透平内部流动计算,可以大大提升燃机的性能.快速准确地预测尾缘劈缝射流参数对叶栅气动性能的影响,对叶片尾缘冷却结构设计具有重要的理论指导意义.
跨音速透平叶栅流动具有复杂的激波波系,激波与边界层和尾迹的相互作用会显著影响叶栅的气动性能和效率.叶片尾缘激波不仅是叶型损失的一个主要来源,而且会引起叶片表面压力脉动,诱发叶片发生振动[2].Denton等[3]预测了跨音速透平中尾缘的损失,预测结果显示其占透平总损失的1/3左右.尾缘激波撞击相邻叶片吸力面,使边界层发生分离,熵显著增加.尾缘激波会使叶栅气动损失增加,而尾缘劈缝结构既能冷却叶片尾缘,也能对尾缘激波结构产生一定的影响.
通过尾缘劈缝射流引入较低温度的气体来冷却叶片尾缘,可将尾缘温度控制在材料的许可温度以下,避免叶片表面因温度分布不均匀而产生热应力,以保证叶片能安全、长时间工作.Deckers等[4]的研究结果表明,流场压力分布和激波位置的改变会导致叶片尾缘的压力发生变化,射流温度对压力分布和气动损失的影响不大,有劈缝射流的厚尾缘的气动损失比无劈缝薄尾缘的气动损失更小.Wang等[5]认为吹风比的变化对叶片表面马赫数分布的影响很小.Sieverding[6]在研究中发现,随着马赫数从0.96增大到1.34,激波在叶片吸力面上的入射点位置向上游移动了叶片弦长的1%~2%,尾缘射流对尾缘激波强度的影响不大.Rehder[7]的研究表明,激波损失和边界层损失是叶栅总损失的重要组成部分,但尾缘射流对激波损失和边界层损失的影响很小. Laskowski等[8]分别采用定常和非定常数值计算得到跨音速带冷气喷射的透平导叶尾迹流场,结果表明尾缘激波强度随冷气喷射量的增加而减弱.Saracoglu等[2,9]也认为尾缘射流削弱了激波对相邻叶片的作用.综上可知,叶片尾缘劈缝射流能够降低气动损失,但有关尾缘劈缝射流影响尾缘激波强度的机制目前尚有不同的认识,还有待进一步深入研究.
笔者基于Sieverding[6]实验中的跨音速导叶,采用数值模拟方法研究了透平叶片尾缘劈缝射流对尾缘激波结构、尾迹流场特征及气动性能的影响,尽可能保证数值模拟工况与实验工况一致.在相同出口马赫数下,比较不同射流进口总压对叶栅内部激波和气动性能的影响,以期为优化尾缘劈缝射流参数、降低跨音速叶栅气动损失和改善高负荷透平叶栅性能提供理论指导.
1 数值计算方法
1.1 计算模型与边界条件
笔者参照图1(a)所示的Sieverding[6]实验中的叶型建立计算模型,图1(b)为笔者计算采用的尾缘射流叶型,其几何参数见表1,图中的Cax为轴向弦长.因为采用二维数值模拟[10],故可将原叶片模型进行简化,取消射流进口位置的圆柱腔室,采用一段截面作为射流进口.计算工况如表2所示,计算域周向使用周期性边界条件,参照实验工况设定叶片表面为绝热边界.
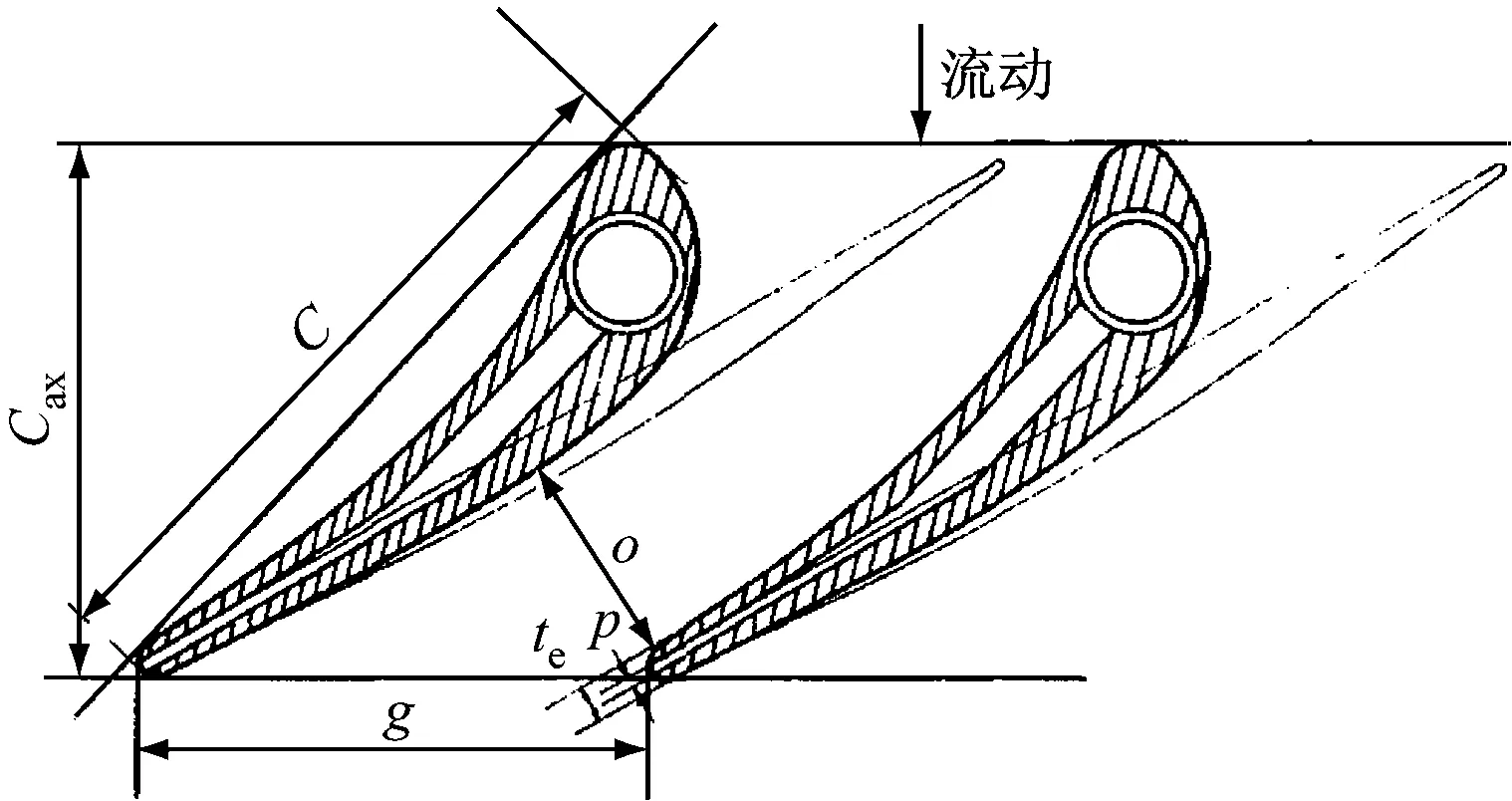
(a) 实验叶型[6]

(b) 尾缘对开缝叶型
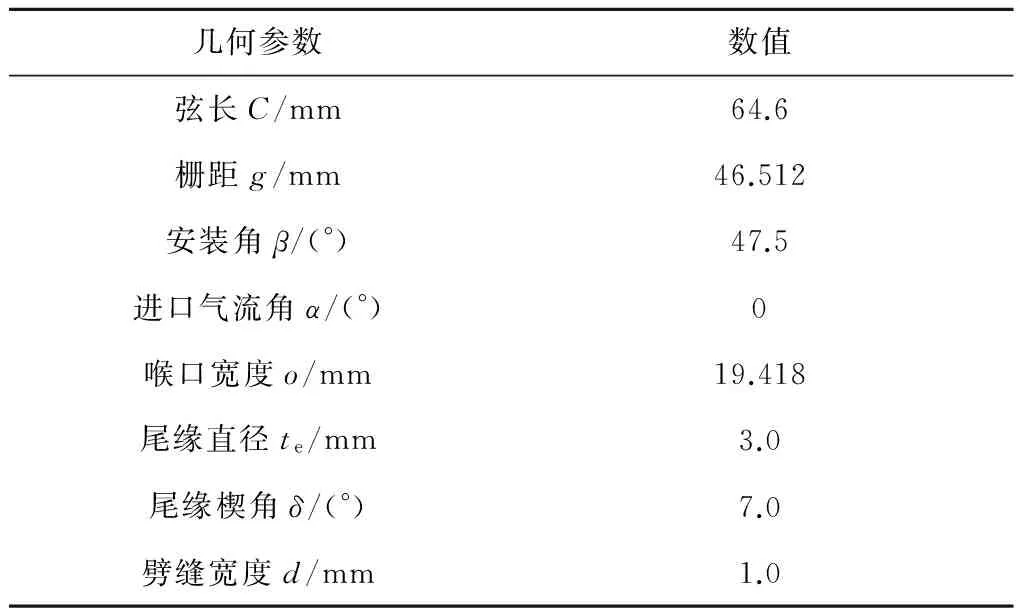
几何参数数值弦长C/mm64.6栅距g/mm46.512安装角β/(°)47.5进口气流角α/(°)0喉口宽度o/mm19.418尾缘直径te/mm3.0尾缘楔角δ/(°)7.0劈缝宽度d/mm1.0
1.2 网格验证
模拟计算采用结构化网格,拓扑结构采用“HOH”结构.计算域入口距叶片前缘为1倍弦长,计算域出口距叶栅尾缘为3倍弦长,边界层网格节点数为40个,增长比为1.05.叶片尾缘处网格示意图如图2所示.通过3套不同数量的网格,采用S-A湍流模型计算无劈缝叶型,叶片表面的等熵马赫数分布如图3所示,压力面上的计算结果与实验结果总体吻合较好,吸力面上等熵马赫数的计算结果与实验结果大体趋势一致,但在20%~30%弦长处,实验得到的波前马赫数高于模拟计算得到的马赫数.这可能是因为实验采用压力探针,能精确测到叶片表面的压力,但定常数值模拟对叶片表面压力分布的计算与y+有关.结合表3可知,网格B和网格C下叶栅出口气流角、波前马赫数及激波位置的预测结果基本相同,说明网格B可以满足求解精度的要求.

表2 数值模拟工况

(a)无劈缝(b)对开缝
图2 叶片尾缘附近网格示意图
Fig.2 Meshing of the area near trailing edge of the blade
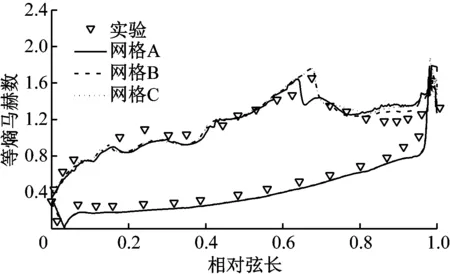
图3 不同网格下叶片表面的等熵马赫数分布
1.3 湍流模型验证
一方程湍流模型是指在湍流平均流动方程的基础上,多求解一个表示湍流黏性的输运方程.近年来,应用较多的一方程湍流模型有Baldwin-Barth(B-B)模型、S-A模型等.这些模型都是直接建立涡团黏性系数输运方程的.相对于两方程湍流模型,S-A模型的计算量较小,稳定性较好,计算网格在物面处不需要很精细,与代数模型的网格量级相当即可.另外,S-A模型方程是“当地”型的,即在某一点上模型方程不受其他点的解影响,适用于结构网格和非结构网格[11].采用S-A模型对二维RAE2822和三维ONERA M6机翼的黏性流场进行数值模拟,结果表明S-A模型能较好地扑捉激波,与实验吻合得较好.在识别激波以及大尺度分离流动时表现较好[12].

表3 网格无关性比较
预测跨音速流动性能的关键是激波扑捉的质量,笔者选择显式AUSM+格式求解可压缩N-S方程,空间上对流动和湍流黏性采用三阶MUSCL差分方式.为了提高计算精度和效率,计算过程中采用多重网格技术,多重网格数为6.在数值求解过程中,方程中每一项的求解残差均设定为10-3,以保证计算严格收敛.
采用4种湍流模型(Standardk-ε、RNGk-ε、Realizablek-ε和S-A)得到的叶片表面等熵马赫数分布如图4所示.与实验值相比,Standardk-ε模型的数值黏性较大,激波被抹平,几乎没有间断.Realizablek-ε模型在45%轴向弦长附近预测到了非物理激波,RNGk-ε、Realizablek-ε和S-A模型预测所得波前马赫数高于实验值,但是激波位置与实验值比较吻合,激波强度(即波前后的速度比)也与实验值比较接近.在压力面的中弦,S-A模型与实验值更接近.综合评价上述4种模型后,认为选择S-A模型比较适宜.

图4 不同湍流模型叶片表面等熵马赫数分布
1.4 各种损失的计算方法
叶型损失主要由边界层损失、激波损失和尾迹掺混损失3部分组成,对于相同的叶型和出口马赫数,在不同射流进口总压下,这3部分损失所占比例会发生变化.因此,正确认识不同射流压比下各部分损失的变化规律对损失的预估及控制是非常有必要的.
从动能损失的角度出发,将各损失进行拆分.叶栅总动能损失为主流和射流进口总压质量加权平均值与流道出口总压平均值之差.总动能损失系数ζtotal定义为
(1)
式中:p01为流道进口总压,Pa;p0j为射流进口总压,Pa;p05为流道出口总压,Pa.
由于边界层的存在,叶片近壁区存在一层低能流体,该部分流体携带的能量与边界层外流体携带能量之差为边界层损失.因此,边界层损失Δe的定义为
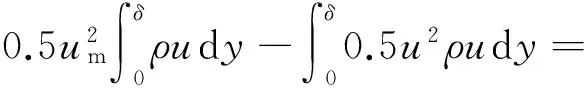
(2)
式中:um为边界层外速度,m/s;u为边界层内速度,m/s;ρ为流体密度,kg/m3;δ为边界层厚度,m.
分别对尾缘附近的压力面和吸力面边界层进行计算,可得总边界层损失.边界层损失系数ζbl定义为
(3)
由激波引起的损失可通过计算激波前后的总压变化得到,激波损失系数ζshock定义为
(4)
式中:p4为激波后静压,Pa;p04为激波后总压,Pa;p03为激波前总压,Pa;γ为比热容比.
尾迹掺混损失由总动能损失减去边界层损失和激波损失后得到,所以尾迹掺混损失系数ζml定义为
ζml=ζtotal-ζbl-ζshock
(5)
2 计算结果与分析
2.1 激波结构
图5为叶片表面等熵马赫数分布.由图5可以看出,与无劈缝工况相比,有劈缝射流时的波前马赫数和激波前后速度比均较低,说明劈缝射流使作用于吸力面的激波强度降低;射流压比为0.50时激波强度最小;随着射流压比增大,作用于吸力面的激波强度也逐渐增强.有劈缝射流时,激波在吸力面入射点的位置向前缘移动;Sieverding[6]的实验结果也有类似现象.

图5 叶片表面等熵马赫数分布
图6为尾缘下游2倍尾缘直径处等熵马赫数沿尾缘法向的分布.劈缝射流使尾缘燕尾波的位置向上游偏转,燕尾波张角增大,也使燕尾波的波前马赫数减小,使激波强度减弱,但射流对压力面燕尾波强度的削弱作用更明显,使吸力面侧燕尾波强度略高于压力面侧燕尾波强度.分析不同射流压比可以发现,射流压比为0.50时波前后速度比最小,激波强度最弱,燕尾波张角最大;继续增大射流压比,燕尾波强度与张角的变化不明显.无劈缝射流时,尾迹区吸力面和压力面侧均存在低速峰值,且尾迹区的速度分布不均匀,这会使剪切掺混作用加强;尾缘射流可以弥补尾迹区的速度亏损,使尾迹区的速度分布基本均匀.
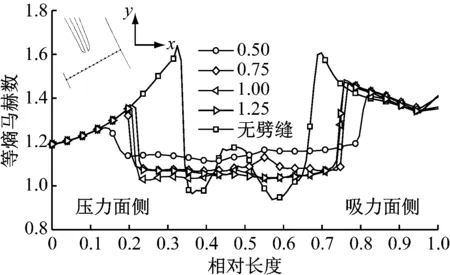
图6 尾迹区等熵马赫数沿尾缘法向的分布
图7为数值纹影与尾缘附近流线分布.由图7可知,无劈缝射流时,尾迹区低动量流体与主流发生剪切掺混形成脱落涡,使流线发生扭曲,在紧靠尾缘附近出现回流区,漩涡和回流区使尾迹区的压力低于主流区的压力,在压力梯度作用下形成燕尾波,而且尾迹流向长度较大,导致激波脱体.射流可为低能尾迹注入额外动量,使尾迹压力回升,尾迹与主流侧的压力梯度减小,低动量流体的分布区域由无劈缝射流时的整个尾缘后流场变为压力面和吸力面尾缘后的局部区域,从而导致燕尾波强度减弱,燕尾波形成位置偏向上游,燕尾波张角增大.从图6可以发现,射流对压力面侧激波强度的削弱作用更大,这是由于尾缘吸力面和压力面侧的边界层厚度与能量不同,尾缘吸力面侧的边界层相对较厚,剪切、拖拽作用使射流向下游运动时偏向吸力面侧,从而更易于带走压力面侧的低动量流体,使压力面侧尾缘后的压力分布更加均匀.压比为0.50时,压力面侧尾缘后的流场更加均匀,激波强度最小.
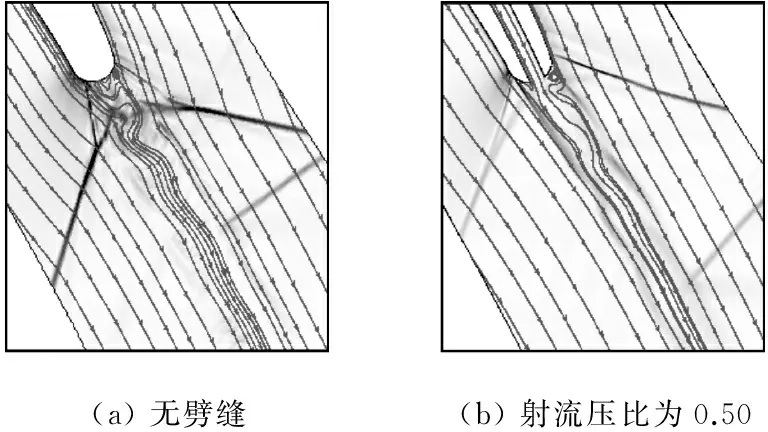
(a)无劈缝(b)射流压比为0.50
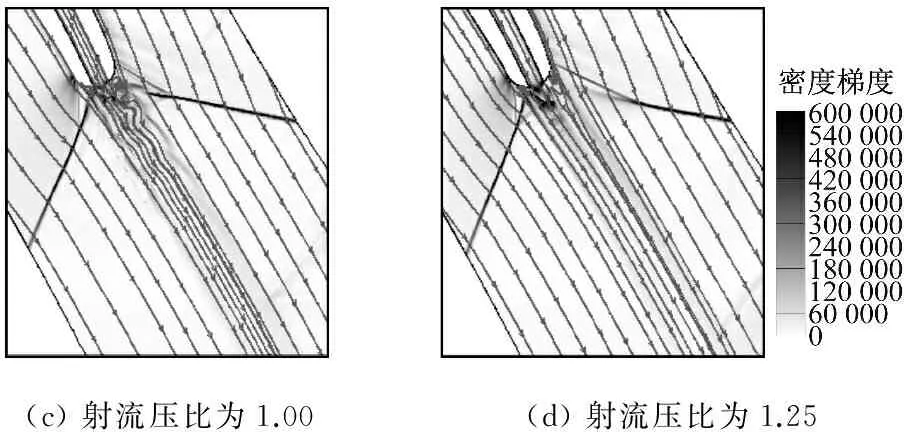
(c)射流压比为1.00(d)射流压比为1.25
图7 数值纹影与流线分布
Fig.7 Shock wave structure and streamline distribution
2.2 尾迹形态
为了研究劈缝射流对速度尾迹的影响规律,分别在叶栅出口1.1Cax、1.2Cax和1.3Cax处沿周向提取速度的大小.图8为速度尾迹沿栅距的分布曲线,采用无劈缝叶栅出口截面处的平均速度对提取的速度进行无量纲化.无劈缝射流时,尾迹低速峰值和尾迹宽度最大.有劈缝射流时,尾迹低速峰值降低且分布位置略偏向吸力面侧;压比为0.50时,1.1Cax处的尾迹宽度较大,速度分布最均匀,均匀流场中的压力梯度较小,使得尾缘燕尾波的强度相对较弱;射流压比为1.25时,尾迹宽度最小,在1.2Cax及下游位置处的低速峰值最小,有利于降低尾迹掺混损失.
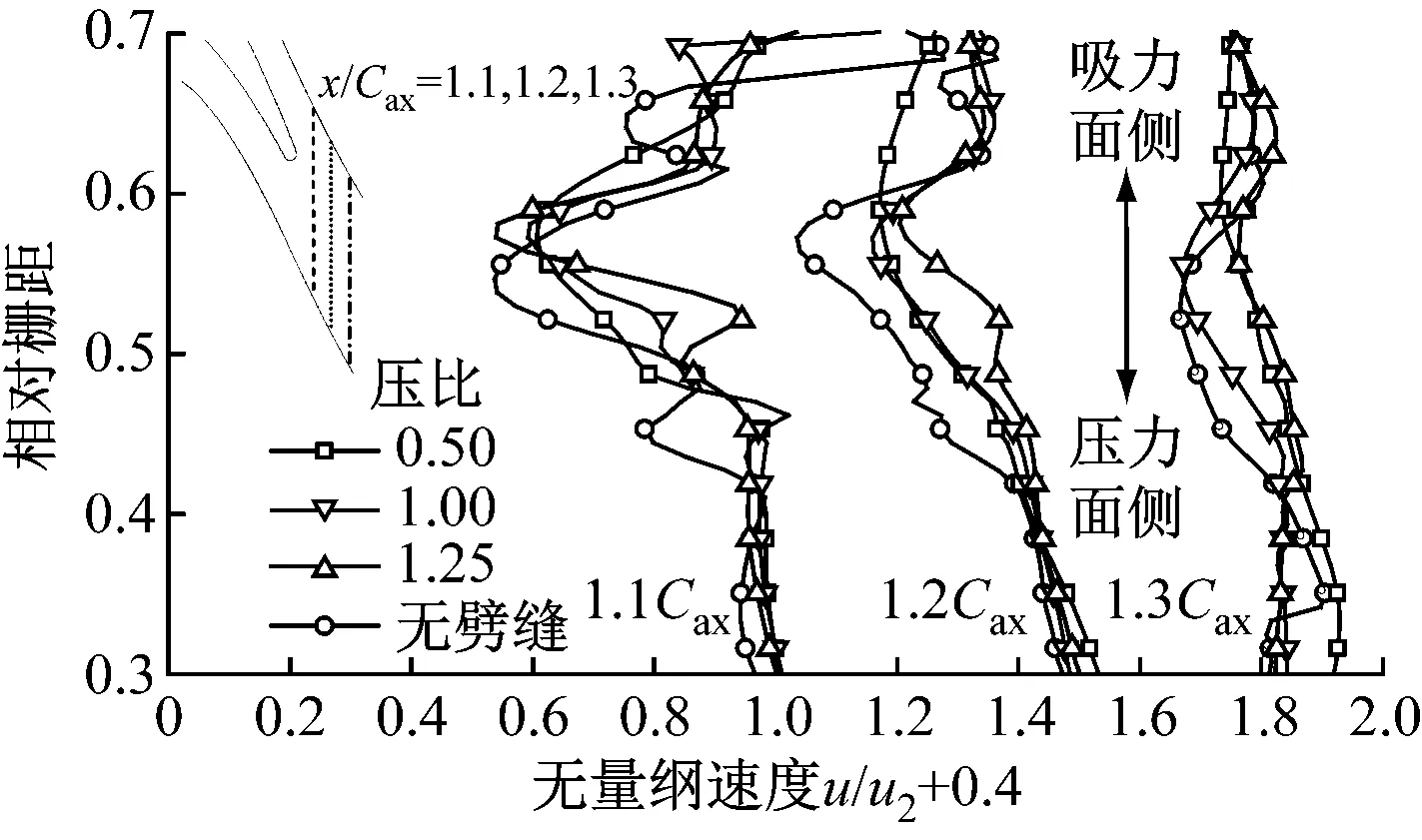
图8 速度尾迹分布曲线
2.3 叶栅动能损失
图9为不同射流压比时叶栅的各种能量损失系数分布,并给出射流压比与吹风比的对应关系.当尾缘无射流时,叶栅的总动能损失及各种损失均较大.劈缝射流可以降低激波损失和尾迹掺混损失,射流压比为0.50时叶栅动能损失最小.随着射流压比从0.50增大到1.25,激波损失逐渐增大,尾迹掺混损失逐渐减小.由射流压比与吹风比的关系可知,射流压比为1.25时吹风比最接近1.0.结合图8可知,射流对尾迹区动量的补充能力更大,使尾迹宽度和速度最低值均较小,最大程度地降低了尾迹掺混损失.劈缝射流及不同射流压比对边界层损失的影响很小,这与Rehder[7]的结论一致.
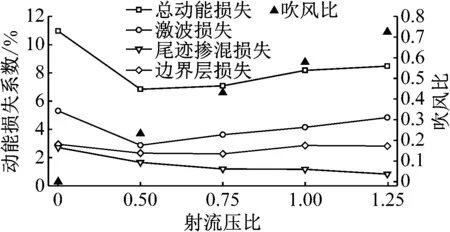
图9 动能损失系数分布及吹风比
3 结 论
(1) 采用定常S-A模型对跨音速叶栅气动性能进行计算,得到的计算结果与实验值的偏差较小,该方法可快速获得叶栅的整体气动性能.
(2) 劈缝射流可以减小尾迹宽度与低速峰值,使尾迹流场的分布比较均匀,尾缘燕尾波强度减弱,射流向下游运动略偏向吸力面侧,导致射流对压力面侧激波强度的削弱作用更大;射流通过改变尾迹低能流体的分布区域,使燕尾波的形成位置更贴近尾缘,激波张角增大.
(3) 劈缝射流可以降低激波损失和尾迹掺混损失,但对边界层损失的影响不大,因而导致叶栅的总动能损失降低;随着射流压比增大,激波损失逐渐增大,尾迹掺混损失逐渐减小,当射流压比为0.50时,叶栅的总动能损失最小.
[1] DENTON J D. The 1993 IGTI scholar lecture: loss mechanisms in turbomachines[J].JournalofTurbomachinery, 1993, 115(4): 621.
[2] SARACOGLU B H, PANIAGUA G, SALVADORI S, et al. Trailing edge shock modulation by pulsating coolant ejection[J].AppliedThermalEngineering, 2012, 48: 1-10.
[3] DENTON J D, XU L. The trailing edge loss of transonic turbine blades[J].JournalofTurbomachinery, 1990, 112(2): 277-285.
[4] DECKERS M, DENTON J D. The aerodynamics of trailing-edge-cooled transonic turbine blades: part 1—experimental approach[C]//ASME1997InternationalGasTurbineandAeroengineCongressandExhibition. Orlando, Florida, USA: American Society of Mechanical Engineers, 1997.
[5] WANG Yanggang, ZHAO Longbo. Investigation on the effect of trailing edge ejection on a turbine cascade[J].AppliedMathematicalModelling, 2013, 37(9): 6254-6265.
[6] SIEVERDING C H. The influence of trailing edge ejection on the base pressure in transonic turbine cascades[J].JournalofEngineeringforPower, 1983, 105(2): 215-222.
[7] REHDER H J. Investigation of trailing edge cooling concepts in a high pressure turbine cascade-aerodynamic experiments and loss analysis[J].JournalofTurbomachinery, 2012, 134(5): 051029.
[8] LASKOWSKI G M, FELTEN F N. Steady and unsteady CFD simulations of transonic turbine vane weaks with trailing edge cooling[C]//VEuropeanConferenceonComputationalFluidDynamics. Lisbon, Portugal: [s.n.],2010: 1-14.
[9] SARACOGLU B H, PANIAGUA G, SANCHEZ J, et al. Effects of blunt trailing edge flow discharge in supersonic regime[J].Computers&Fluids, 2013, 88: 200-209.
[10] 轩笠铭, 陈榴, 杨玉骏, 等. 尾迹作用下叶片表面非定常传热特性的数值分析[J].动力工程学报, 2017, 37(5): 361-366.
XUAN Liming, CHEN Liu, YANG Yujun, et al. Numerical analysis of heat transfer characteristics on turbine blade surface under the action of unsteady wakes[J].JournalofChineseSocietyofPowerEngineering, 2017, 37(5): 361-366.
[11] 李广宁, 李杰, 李凤蔚. S-A湍流模型在N-S方程求解中的应用研究[J].弹箭与制导学报, 2006, 26(2): 1180-1182, 1186.
LI Guangning, LI Jie, LI Fengwei. Application of S-A turbulence model in N-S equation solutions[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2006, 26(2): 1180-1182, 1186.
[12] 高歌, 闫文辉, 吴俊宏, 等. 计算流体力学——典型算法与算例[M]. 北京: 机械工业出版社, 2015.
