波纹钢腹板等截面箱梁横隔板位置研究

甘肃省交通规划勘察设计院股份有限公司 甘肃 兰州 730030

正文：

0 引言

随着科技的发展和新材料、新工艺的推广应用，近年来我国桥梁的跨越能力也在不断的突破，但同时随着桥梁跨径的不断增大，桥梁上部结构恒载占总荷载的比例也在提高，桥梁自重已成为制约其跨越能力的主要问题。与传统的混凝土箱梁结构相比，箱梁腹板采用波纹钢腹板一是可以使上部结构箱梁自重减轻、恒载内力减小；二是波纹钢腹板在轴向为折叠状，当受到轴向预压力作用时钢腹板能自由压缩，使其对顶、底混凝土板由于徐变和收缩而产生的变形约束较小，可对箱梁施加有效的体外预应力[1]。从波纹钢腹板箱梁的构造可以发现，主梁竖向剪力全部由波形钢腹板承受，而主梁弯曲正应力主要由混凝土顶、底板承担，对于波纹钢腹板箱梁来说，在荷载作用下，波形钢腹板的竖向剪应力大小以及其沿横向的分布情况是应该被桥梁设计者去关注和研究。

本文主要给出构造合理的箱梁横隔板布置，达到各钢腹板的竖向剪应力在桥梁纵、横向分布均匀，峰值最小的目的。

1 工程概况

某公路桥梁上部结构采用波纹钢腹板连续箱梁，桥跨布置为4×30m，双向6车道。主梁为单箱四室等高截面，箱梁顶宽25.3m,底板宽19.3m,梁高2.2m，箱梁顶板设置成2%双向横坡,箱梁顶板厚28cm，底板厚25cm，波纹钢腹板厚1.6cm，每跨设置两道横隔板，横隔板厚30cm。桥梁设计荷载为公路-Ⅰ级，二期恒载120kN/m。主梁顶、底板和横隔板均采用C55混凝土，波纹钢腹板采用Q345E钢。桥梁单跨30m平面构造如图1。这里要说明的是，图1中横隔板的位置是初始设定的，并不是最终的优化结果，在进行横隔板位置优化计算后给出最佳结果。

图1 桥梁单跨30m平面构造图(cm)

2 建立有限元模型

采用大型通用有限元分析软件ANSYS建立分析模型，由于桥梁4跨构造一致，只取一跨建模计算。波纹钢腹板单箱多室箱梁的顶、底板均为混凝土结构，采用混凝土实体单元来建模。为达到波纹钢腹板与混凝土共同作用的结果，在单元划分时要使对应位置的波纹钢腹板节点与混凝土单元节点重合，保证波纹钢腹板与混凝土充分粘结。波纹钢腹板采用板壳单元来模拟，建模时应保证钢腹板与上、下翼板的节点吻合，让波纹钢腹板的波折线与顶板、底板混凝土完全重合；横隔板采用三维实体单元模拟，上、下翼板与横隔板的连接方式采用共节点[2]。

在模型中荷载组合为：梁体自重、二期恒载、单向3车道加载公路-Ⅰ级车道荷载。由于只取一跨建模计算，边界条件按简支处理。桥梁上部结构有限元计算模型和波纹钢腹板有限元模型如图2、图3所示。

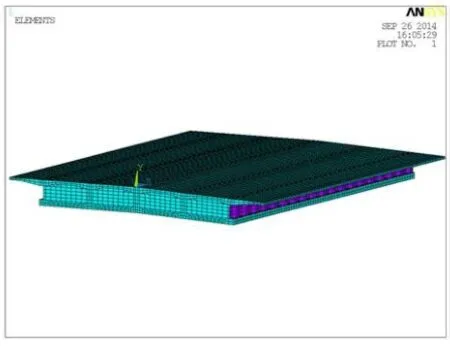
图2 桥梁上部结构有限元模型

图3 波纹钢腹板有限元模型

3 横隔板不同位置所对应的波纹钢腹板竖向剪应力

在ANSYS后处理中，通过ANSYS APDL参数化编程提取各钢腹板竖向剪应力[3]。在不同的横隔板位置下各片钢腹板沿桥梁纵向剪应力值数据如表所示。

横隔板不同位置所对应的各片钢腹板沿桥梁纵向剪应力最大值表

上表第2组横隔板1中心位置8.5m和横隔板2中心位置21.5m与图1中设计初始横隔板位置相对应，从表中数据分析，在第2组位置下计算出的每片波纹钢腹板剪应力值均较大，为达到每片波纹钢腹板竖向剪应力沿桥梁纵向分布均匀，同时峰值较小的理想状态，将图1中2道横隔板的位置同时按差值0.8m进行调整再计算剪应力最大值。通过分析调整后计算得到数据发现，在第4组中，2#、3#钢腹板计算所得竖向剪应力峰值最小 ；在第3组中，1#、4#、5#钢腹板计算所得竖向剪应力峰值最小；在第1组中1#、5#钢腹板剪应力峰值最小，但与2#、3#、4#钢腹板剪应力最大值相差较大；在第5组中2#、3#钢腹板剪应力峰值最小，但该组中峰值普遍偏大；通过四组中各剪应力峰值大小的比较，发现第3组数据中3#钢腹板竖向剪应力最大，最大值为122.326MPa，而第4组中4#钢腹板竖向剪应力最大，最大值为116.46MPa，且5片钢腹板的剪应力峰值分布均匀，可见第4组中的2道横隔板位置设计较为合理。

4 结论

波纹钢腹板单箱多室箱梁结构受力复杂，通过横隔板设置不仅可以提高桥梁上部结构的扭转刚度[4]，同时横隔板位置合理的设计，对于改善钢腹板的受力状态也是非常重要的。本文通过横隔板纵向位置的调整试算，计算分析了横隔板设置位置与钢腹板剪应力之间的变化情况，较好的得到波纹钢腹板剪应力分布规律。