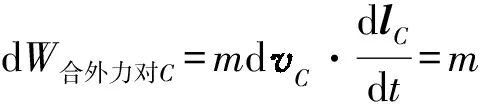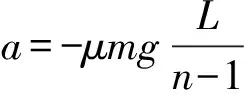用质心动能定理巧解一道竞赛题

周碧华

(上饶中学,江西 上饶 334000)

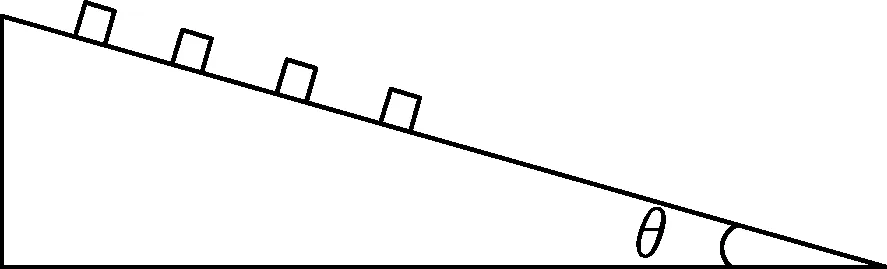
原题.某根水平固定的长滑竿上有n(n≥3)个质量相同的滑扣(即可以滑动的圆环),每个相邻的两个滑扣(极薄)之间有不可伸长的柔软轻质细线相连,细线长度均为L,滑扣在滑竿上滑行的阻力大小恒为滑扣对滑竿正压力大小的μ倍.开始时所有滑扣可近似地看成挨在一起(但未相互挤压);今给第1个滑扣一个初速度使其在滑竿上开始向左滑行(平动);在滑扣滑行的过程中,前、后滑扣之间的细线拉紧后都以共同的速度向前滑行,但最后一个(即第n个)滑扣固定在滑竿边缘.已知从第1个滑扣开始的(n-1)个滑扣相互之间都依次拉紧,继续滑行距离l(0

此题参考答案的解法非常繁杂,在此不再赘述,下面我们先介绍质心动能定理.

惯性系中对质心有

(1)

合外力对质心做的功

(2)

由(2)式得

(3)

(3) 式左右两边积分得

W合外力对C=ΔEkC.

(4)

(4) 式就是质心动能定理:合外力对质心所做的功等于质心动能的增加量.我们就用质心动能定理来解此题,设每个滑扣的质量为m,滑扣1的初速度大小为v0,对前面(n-1)个滑扣,设合外力对其质心做的功为W,则有

前(n-1)个滑扣质心动能的增量为

W=a[12+22+32+…+(n-2)2]-

μ(n-1)mgl.

(5)

利用数学公式

12+22+32+…+N2=

(6)

由(5)、(6)式及质心动能定理得

(7)

(8)

我们发现此题用质心动能定理几乎是“秒解”,为了让学生更好地掌握质心动能定理,我们再举一例.

图2

变式.4个完全相同的小物体(可看作质点),等间距静止在固定的斜面上,间距为d,斜面的倾角为θ,小物体与斜面间的动摩擦因数为μ,现给最上面的物体一个沿斜面向下的初速度v0,小物体间将发生的碰撞都是完全非弹性的,求v0满足什么条件,最后上面3个小物体恰好停在最下面的小物体处.(如图2)

解析:设每个小物体的质量为m,对4个小物体,用质心动能定理有

(9)

由(9)式整理得

(10)

小结:对于多个质点构成的质点系,若过程复杂,比如多次碰撞,如果质点系所受到的合外力已知,且合外力对质心做功可求,我们就可以利用质心动能定理,巧妙地避开质点系内力做功的复杂计算,从而可以快速轻松地求解相关问题,在竞赛辅导中有效地开阔学生的视野,激发学生学习物理竞赛的兴趣,发展学生的思维品质.