问题引导下的尝试策略在教学中的应用
——以“匀变速直线运动的速度与位移的关系”为例
2018-03-06潘华君顾爱芬
潘华君 姜 胜 顾爱芬
(江苏省宜兴第一中学,江苏 宜兴 214200)
1 尝试教学简介
尝试教学是一种教学理念,一种教学方式,更是一种教学精神,[1]其实质,就是让学生在一定的问题情景中主动尝试,通过对“预设问题”的不断“试错”从而生成新问题,在生本、生生、师生的多向交流中获得成功.江苏省常州市教育科学研究院院长邱学华先生设计的基本模式有7个环节:准备练习—出示尝试题—自学课本—尝试练习—学生讨论—教师讲解—第二次尝试练习.[1]在此基础上,亦有人提出了多种模式.但无论何种模式,其核心是让学生自己阅读和思考.[2]另一方面,苏联教学论专家马赫穆托夫等人创立的“问题教学理论”认为:人们在认识活动中,当遇到现有条件或已有的经验尚无法解决的实际问题时,就会产生一种怀疑、探索的心理状态,从而激活主体思维,试图去找出解决问题的办法.[3]基于此,结合两者优点的问题引导下的尝试教学法,以问题引导为教师“导”的方式,以尝试为学生“学”的具体操作方式,让学生在实践中获取知识,在体验中感知成功的乐趣,从而培养学生敢于探究、勇于实践的科学素养.下文就以“匀变速直线运动的速度与位移的关系”新课教学为例,做一次教学尝试.
2 问题引导下的尝试教学法的实践应用
2.1 尝试感知两物理量间的定性关系
师:播放交警在车祸现场测量的图片.交警从刹车痕迹的长短可以判断当时车速的大小: ① 假如我们把汽车刹车的过程看成是一个匀减速运动的过程,此处的刹车痕迹代表了哪一个物理量? ② 从物理学的角度看,这种判断的依据是什么?
生:此处痕迹表示刹车过程中汽车的位移;在加速度一定的前提下,初速度越大,刹车时间越长,位移也就越大.
师:通过上述实例的分析,我们明确了匀变速直线运动中的速度与位移的定性关系,那么这两者间的定量关系是怎样的呢?这就是本节的主题.
设计理由:本节课,以一张“交警在车祸现场处理”的图片引入,其目的有: ① 相较于人教版以“子弹从枪筒里射出”为例,本节课的引入更接近学生的生活,更能在新课的开始吸引学生的眼球,把学生的注意力和思绪拉回课堂; ② 以图片入手,可以培养学生的观察能力以及构建理想运动模型的能力; ③ 以客观的现实,引发学生的对行车安全的思考,将“安全行车、尊重生命”蕴含于本节课中; ④ 通过师生的问答方式,在学生感知定性关系后,抛出新问题——寻找定性关系.
2.2 尝试寻找两物理量的定量关系
师:若汽车在做匀加速直线运动,初速度为5 m/s,加速度大小为1 m/s2,则当位移为100 m时,末速度多大?(只要求学生画出运动示意图、思考解决的方法,不需要具体的解答.)
生A:先通过位移与时间的关系式求出运动时间t,然后将t代入速度与时间的关系式求出末速度.
师:A同学的思路完全正确.在他的方法中,为了求出末速度,先求了一个运动的时间,即运动时间t仅是起到一个桥梁的作用,联系着“速度与时间的关系式”和“位移与时间的关系式”,这样的方法正确但略显复杂.我们能不能找一个更简单的处理方法,即能不能直接找出一个速度与位移的关系式?如何找这个公式?
生B:只要把t消掉就可以直接推导出速度与位移的关系式.
师:好,我们就按照B同学的方法,请同学自行推导匀变速直线运动的速度与位移的关系式,并于同桌相互交流.(学生自行推导,教师在教室里巡查,注意收集学生的典型错误;待学生推导好后,投影学生的作答)
设计理由: ① 通过一道例题的设计,教师通过恰当的引导,让学生意思到用已有的知识求解时较为复杂,从引导学生思考“时间t的作用”和“有没有更简单的处理方法”,从而寻找到“消元”的方法,为得出定量关系式打下基础.② 与人教版本节教材上例1的一个区别是,在设计本题时赋予其一个初速度.这是因为,基于以往的教学经验,若设计一个初速度为0的匀加速运动,部分学生在自行推导公式时,往往就会直接推导初速度为0条件下的速度与位移的关系式.为了避免以上情况,同时使推导式更具有一般性,特作以上修改.③ 从一线教学现场观察发现,学生的数学运算能力比较弱,本尝试题的设计目的就在于给予学生思考、分析、运算的时间,让学生的思维在“慢教学”的过程中逐渐向深处延伸.④ 在学生的求解中,还有少部分学生会先从位移公式入手,利用求根公式求出时间的表达式再代入速度公式,这个求解方式既复杂又难以得到最终需要的表达式,教学中建议要适当引导.
2.3 尝试应用,加深理解
师:同学们通过消元法推导出了匀变速直线运动速度与位移的关系式:2ax=vt2-v02.结合上节课所学的位移与时间的关系式以及做过的习题,请你思考一下,在哪些情景中,利用速度与位移的关系式求解更简洁?
生:这个表达式涉及的物理量有加速度、位移、初末速度,不涉及时间,因此,该表达式主要用于题目中不涉及时间的问题.
师:是的,这个表达式提出的目的就是在于解决不涉及时间或者是时间难以测量的问题.例如,这节课开头所展示的“车祸现场”的图片,车祸发生于“过去时空”且时间短,交警在处理时无法测量时间,此时只能测量位移、估测刹车时的加速度,从而判断刹车前的速度.这也就是该表达式的物理意义所在.
师:请同学们依据前面的分析,选择合适的公式,解决下面这个问题“某汽车在做直线运动,初速度为108 km/h,刹车时的加速度大小为5 m/s2,一段时间后速度减为36 km/h,求汽车在该过程中的位移”.(学生独立作答)
师:(出示教师事先准备好的一份典型的错误解答,如没有统一单位的、没有规定正方向的、加速度没有代入负值的等,进行投影展示)屏幕上展示的是一位同学的解答过程,对比一下你的解答,请同学们来“找茬”?
生C: 我发现它有两个错误: ① 它在进行数值运算时需要统一单位; ② 刹车过程中,汽车在做匀减速运动,加速度应代入负值.
生D:还有一个错误,没有规定正方向.只有规定了正方向,用正负表示矢量的方向才有意义.
师:两位同学思考得很深入.结合两位同学的分析,再看这个表达式2ax=vt2-v02,式中4个量均是矢量,在直线运动问题中,可规定正方向,利用正负表示各个矢量的方向,如以初速度方向为正:加速和减速时,a分别应代入什么值?末速度为正值或负值时,有何意义?位移为正值或负值时,有何意义?
学生齐声回答:加速时a与初速度方向相同,代入正值,减速时a与初速度方向相反,应代入负值;末速度为正值,表示与规定正方向同向,末速度为负值时,表示与规定正方向反向;位移为正值,表示末位置在初位置的正方向前,位移为负值时,末位置在初位置的负方向上.
设计理由: ① 本章教学的一个难点就是公式较多,学生难以快速、正确的选择,通过对两个位移公式的比较,让学生感知“速度与位移关系式”适用的情景,帮助学生逐渐学会选择的依据; ② 运动学问题处理的一个重点就是矢量的处理,在上述设计中,没有直接讨论矢量符号的问题,而是通过一个“减速问题”,让学生“试错”,在尝试中发现问题,在尝试中掌握处理的方法; ③ 此处以预测的典型错误解法让学生“找茬”而不投影学生的错误解答,其目的在于保护学生的积极性,防止出现被投影作业的学生出现难堪等不良情绪.

图1 v-t图
2.4 尝试寻找匀变速直线运动的时空特征
师:物理量间的关系可以通过公式来表达,也可以通过图像来描述,且图像更具有直观性.例如,图1描述的是某一物体在做匀加速直线运动时的v-t图,请你利用图上相关数据求出t时间内的位移和加速度?

师:利用这两个关系式,能不能推导出速度与位移的关系式?
生:利用消元法,消去t即可,如
师:对比两种推导方法,显然第二种方法更简洁.以匀加速直线运动为例,从v-t图可知,速度随时间的变化关系是什么?
生:速度随时间均匀增加.
师:如果以纵轴表示速度,横轴表示位移,v-x图线还是一条直线,即还符合y=kx+b的形式吗?如果不是,如何修改坐标,才能得到直线?
生:不是直线图像了,只有把纵轴修改为v2才会是直线关系.
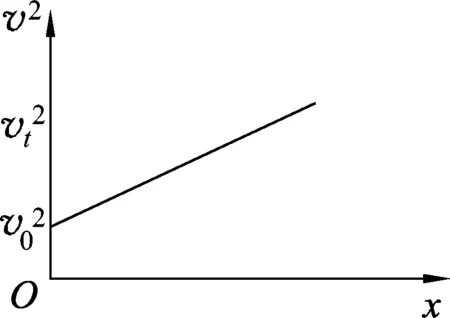
图2 v2-x图
师:从图1和图2可知:从时间角度而言,匀变速直线运动的速度随时间均匀变化,即等时间有相等的速度改变量;从空间角度而言,匀变速直线运动的速度的平方随位移均匀变化,即等位移有相等的v2改变量.[4]这就是匀变速直线运动的时空特征.当然后者相比前者,在描述上略显复杂.通常情况下,我们一般研究的是速度与时间的关系.
设计理由: ① 在上述设计中,速度时间图有两重作用,一是利用速度时间图推导位移公式,让学生感知这一最简洁的推导方法,开拓学生的思维;二是从时间维度分析匀变速直线运动的特征.② 速度位移图的提出,既是与教材中第6节“伽利略对直线运动的研究”相呼应,也是从空间维度分析匀变速直线运动的特征.③ 两张图像相互结合,强化了学生对该类运动特征的认识.④ 通过速度位移图的分析,引导学生学会“化曲为直”的数据处理方法.
3 教学反思
以上,是在高一新授课中采用的问题引导下的尝试教学.从内容看,通过多个尝试问题的设置,既凸显了本章教材的两个重要的思想方法,即矢量处理方法和图像方法,突出了教学的重点,也渗透了安全教育,将教学升格为教育;从操作方式看,它以问题为中心,由预设问题到生成问题,问问相连,步步深入,每一个问题都使学生的思维产生一次飞跃;从教学的实践看,学生课堂的真实参与度高,思维容量较大,有效地提升了学生的分析问题能力和培养了他们敢于实践的科学精神;从课后的检测反馈情况看,学生习得情况良好,有较好的获得感.基于此,这是一次有效的教学尝试.
