碰撞-渐进振动系统的亚谐振动与分岔分析
2018-03-06吕小红
吕小红
1.兰州交通大学机电工程学院,兰州,7300702.甘肃省轨道交通装备系统动力学与可靠性重点实验室,兰州,730070
0 引言
许多动力机械系统中存在的碰撞振动现象使得系统呈现复杂的动力学响应。因此,碰撞振动系统的分岔与混沌的研究[1-6]是近年来机械动力学领域的一个研究热点,同时,碰撞振动现象对工程实际问题的影响[7-10]也引起了很多学者的关注。秦志英等[1]研究了一类分段映射的边界碰撞分岔条件和加周期分岔序列现象。刘莉等[2]应用复合胞坐标系方法研究了Duffing单边碰撞系统的全局分岔特性,讨论了随系统参数的变化而引发的两类激变现象。冯进钤[3]从数值的角度讨论了单边碰撞系统由于擦边周期运动而引发鞍结分岔的机理。王强等[4]应用Floquet理论研究了三自由度碰撞振动系统发生周期倍化分岔的条件以及阻尼对分岔的影响。PETERKA等[5]讨论了两自由度简谐激励碰撞振动系统的各类周期振动在二维参数平面内的存在域及其转迁规律。HUMPHRIES等[6]应用不连续几何的拓扑方法分析了周期激励碰撞振动系统擦边分岔和鞍结分岔之间的关系。李晟等[7]和黑棣等[8]分别研究了两级行星齿轮传动系统和轴承-转子系统的非线性动力学行为。PAVLOVSKAIA等[9-10]研究了冲击钻和钻孔桩等伴随钻进运动的冲击振动机械系统的周期运动与分岔,并讨论了系统参数对钻进率的影响。
电影的“一号角色”只有三个镜头外加一句台词?同一部电影“一号角色”多达几十人?湖南湘潭9岁的何翔和父亲何兴觉得受到了欺诈,将影视公司告上了法庭。在涉事网络电影中,参演的66名小演员都与影视公司签订了合同,根据不同的角色定位,缴纳9800元至29800元不等的费用。何翔一家支付了12800元,获得了参演“一号角色”的机会,但参与拍摄后,发现同为“一号角色”的演员有59人,而且“一号角色”前还有7名“主演”。
本文以小型振动冲击式打桩机为工程背景,建立了同时考虑碰撞振动和渐进运动的碰撞-渐进振动系统的力学模型。研究系统的周期振动在激振频率和预压量参数平面内的存在域及亚谐振动的分岔特点。
1 力学模型和运动微分方程
(1)
j=1,3i=1,2,3,4
式中,Lk为激振器第k次冲击缓冲垫后瞬间滑块的渐进量。
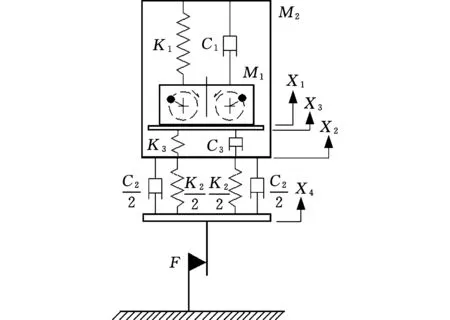
图1 力学模型Fig.1 Mechanical model
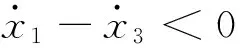
其中,φ(x)是标准正态分布的PDF。每个发电机的成本函数为Cj(Pgen,i),那么发电成本的期望值为:
(2)
(5)激振器擦碰接触缓冲垫→激振器与缓冲垫分离,滑块渐进运动→激振器与缓冲垫分离,滑块静止→激振器冲击缓冲垫;
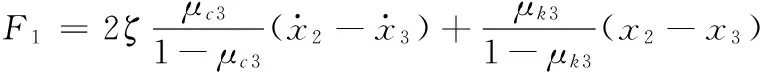
(3)
激振器与缓冲垫黏滞向下运动过程中,F1>0。待F1减小至零时,两者分离。黏滞运动结束瞬间,F1=0,x1=x3+l。黏滞运动结束后,激振器自由振动,缓冲垫在其自身弹性和阻尼的作用下恢复到平衡状态,随质量块一起自由振动。

(6)激振器冲击缓冲垫→黏滞运动,滑块静止→激振器与缓冲垫分离,滑块静止→激振器冲击(或擦碰接触)缓冲垫;等。
膨润土矿床类型分为火山岩型、火山-沉积型、沉积型、侵入岩型四种,以沉积(含火山沉积)型为最多,储量占全部储量的70%以上。膨润土矿的颜色有白色、乳酪色、淡灰色、淡黄绿色、淡红色、褐红色以及黑色、斑杂色等,具有油脂光泽、蜡状光泽或土状光泽,断口常为贝壳状或锯齿状。采出原矿有块状、微层纹状、角砾状、土状及斑杂状等,微细结构以泥质结构为主,也有变余火山碎屑、角砾凝灰及粉砂状结构等。
(4)
当激振器第k次冲击缓冲垫后,两者黏滞向下运动,弹簧K3被压缩,最终使得作用于滑块的合力P0的绝对值增大。当P0满足-P0>f时,滑块克服干摩擦力f渐进运动,渐进的深度为lk,同时系统向下平移lk。当P0的绝对值减小至等于干摩擦力f时,滑块渐进运动过程结束,滑块与周围介质接触面间的摩擦力f由动摩擦力变为静摩擦力,直到滑块开始下一次渐进运动为止。不管滑块处于哪种状态,系统的静平衡位置相对滑块而言都没有改变。
根据上文分析,激振器冲击缓冲垫后,两者或黏滞运动然后分离,或立即分离,直至下次冲击发生。滑块静止或渐进运动。因此,系统在渐进振动过程中可能呈现4种不同的运动状态。每种运动状态的判断条件和运动微分方程如下:
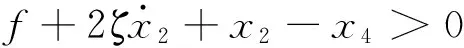
(5)
j=1, 3

据历史考证,我党我军在大革命时期和抗日战争、解放战争的不同阶段曾发行过非常时期的借谷证、米票、粮券等。
(6)
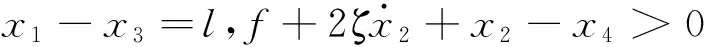
卷积神经网络的训练方法如图2所示,主要由前向传播和反向传播两部分组成。前向传播是样本数据由低层到高层逐层传播的过程,如果前向传播得到的输出值与目标值存在误差,则将误差从高层往低层反向传播回网络中,计算误差梯度,最后利用误差梯度更新卷积神经网络每一层参数的权重,达到自主学习的能力。
罗译:...since he is almost of the same age and as erudite as another man...[6]64
(7)

研究组在采用常规护理的同时,还实施了穴位按摩方法:①选取患者三阴交穴、气海穴以及阴陵泉。②帮助患者选取仰卧体位,由护理人员采用掌根按摩方式对气海穴按摩,按摩次数为36次,用力方向是会阴位置,按摩过程中,应遵循先轻后重原则,在腹部感受到温热感之后即可,然后采用拇指指腹对患者三阴交以及阴陵泉进行按摩,次数同样是36次,频率可根据患者身体状况进行相应的调整,在下肢感受到酸胀即可。
(8)
X′=f(v,X)
(9)

式中,X∈R6;v为实参数,v∈Rm(m=1或2)。
2 相邻两次冲击之间的运动过程
选取一组量纲一参数:μm=0.35,μk1=0.01,μk3=0.7,μc1=0.01,μc3=0.7,ζ=0.1,f=0.5,数值计算各类周期振动在激振频率ω和预压量l参数平面内的存在域,如图2所示。图中不同类型的周期振动用不同的颜色区分,并标注有符号p/n。在没有标注符号p/n的浅色区域,系统主要呈现复杂运动(长周期多冲击运动或混沌)。
凡事都是有个概率问题,任何疫苗不可能100%有效的,并且都是会有部分不良反应的,发烧最常见,特别是麻疹、百白破。接种疫苗10几天内出现症状,特别是疫苗预防病的原发病的相关症状,都应该首先怀疑是疫苗反应。
(4)激振器冲击缓冲垫→黏滞运动,滑块渐进运动→激振器与缓冲垫分离,滑块渐进运动→激振器冲击(或擦碰接触)缓冲垫;
(2)激振器冲击缓冲垫→黏滞运动,滑块静止→黏滞运动,滑块渐进运动→激振器与缓冲垫分离,滑块渐进运动→激振器冲击(或擦碰接触)缓冲垫;
某天下午,我终于找到了和她拉呱儿的机会。珊德拉夫人托着咖啡杯盏走到我的桌边,颔首问,我可以坐在这里吗?
(3)激振器冲击缓冲垫→黏滞运动,滑块渐进运动→激振器与缓冲垫分离,滑块渐进运动→激振器与缓冲垫分离,滑块静止→激振器冲击缓冲垫;
(1)激振器冲击缓冲垫→黏滞运动,滑块静止→黏滞运动,滑块渐进运动→激振器与缓冲垫分离,滑块渐进运动→激振器与缓冲垫分离,滑块静止→激振器冲击缓冲垫;
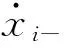
用P0表示作用于滑块的弹性恢复力和阻尼力的合力,有
3 亚谐振动及其分岔特点
选取Poincaré映射σp的状态为系统运动的初始条件,来分析系统在相邻两次冲击之间的运动过程。由于系统可能呈现4种不同的运动状态,因此,在相邻两次冲击之间,系统的运动是4种情形的一系列组合,表现出多重分段性的特征。在相邻两次冲击之间,可能存在以下运动过程:
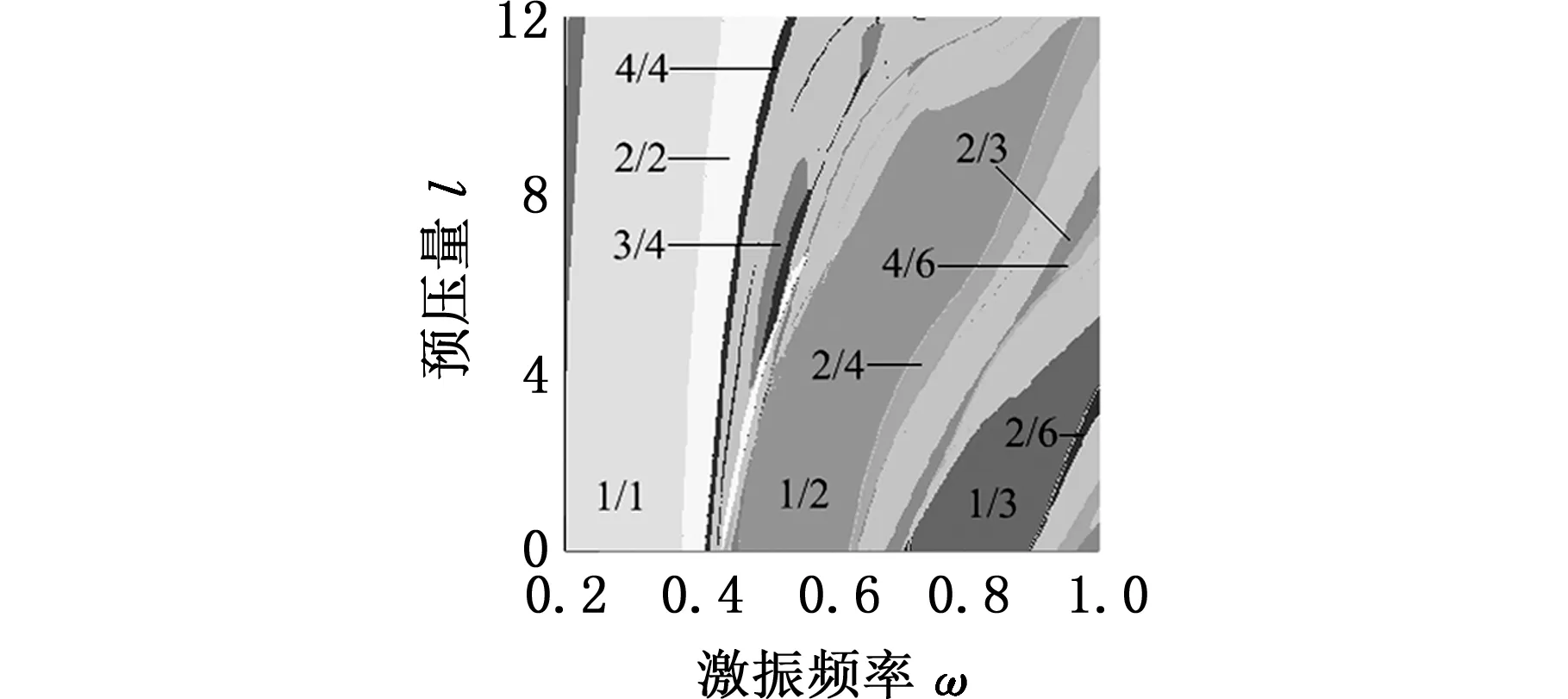
图2 二维参数分岔图Fig.2 Two-dimensional parameter bifurcation diagram
在图2所示二维参数平面内,系统主要呈现1/n单碰周期振动。预压量l不影响1/1周期振动的分岔特点。ω增大,1/1周期振动经倍周期序列通向混沌。但是,预压量l对1/n亚谐振动的分岔过程的影响比较大。图3为图2中1/2亚谐振动和1/3亚谐振动的分岔过程的放大图。当l在0~10范围内变化时,1/2亚谐振动向复杂运动转迁的过程有3种情况,分别对应很小的l区间(大约l∈(0, 2.16)),小l区间(大约l∈(2.16, 4.62))和大l区间(大约l∈(4.62, 10)),见图3a。分别以l=1.5, 4.0,7.0为例,图4给出了3种转迁过程的单参数分岔图。
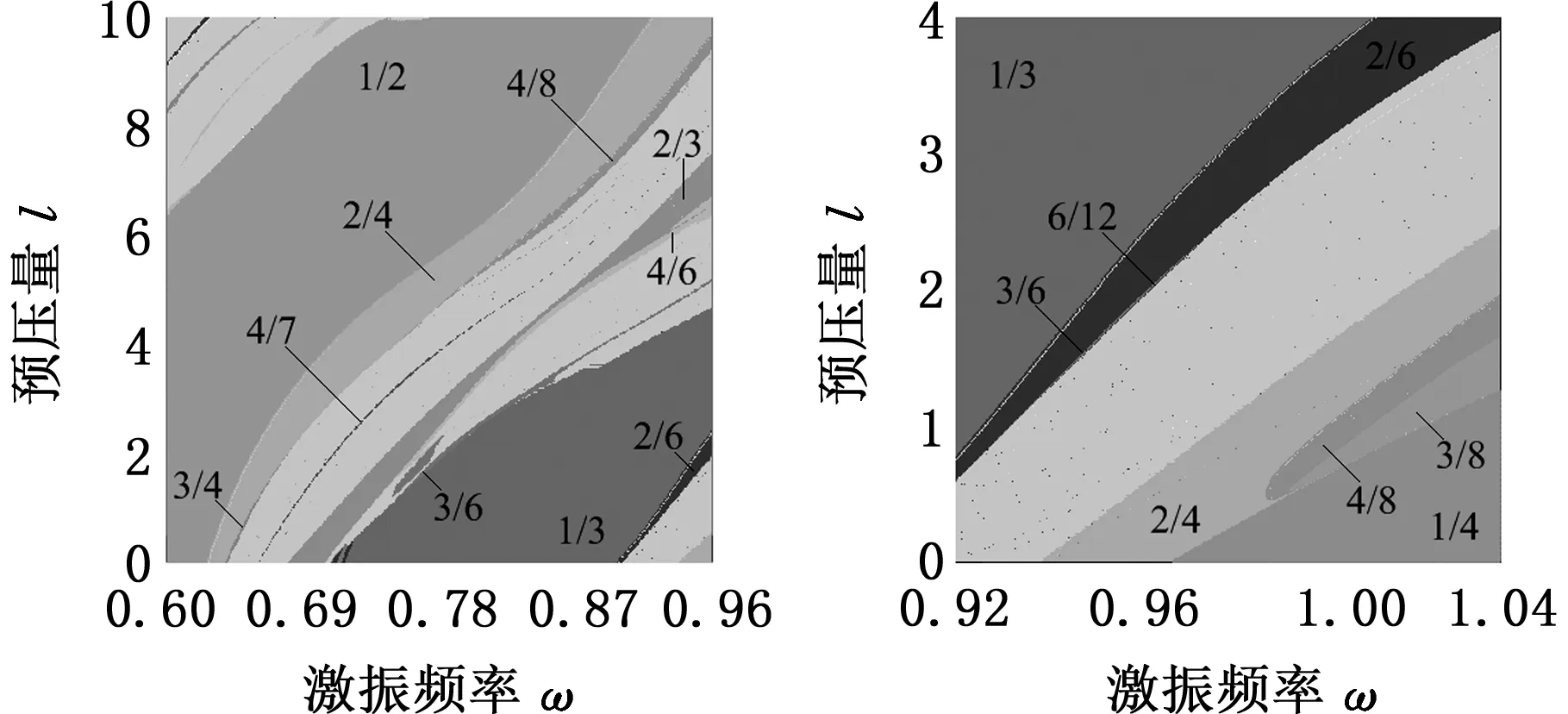
(a)1/2亚谐振动的分岔(b) 1/3亚谐振动的分岔图3 二维参数分岔图的局部放大Fig.3 Local enlargement of two-dimensional parameter bifurcation diagram

(a)小l区域内1/2亚谐振动的分岔(l=1.5)

(b)ω增大时的分岔图(l=4.0)(c)ω减小时的分岔图(l=4.0)

(d)大l区域内1/2亚谐振动的分岔(l=7.0)图4 分岔图Fig.4 Bifurcation diagrams
由图3a和图4a可以看出,在小l区域内,1/2亚谐振动依次经周期倍化分岔、实擦边分岔、周期倍化分岔、鞍结分岔、周期倍化分岔等,最终变为复杂运动。图5清楚地显示了这一复杂的分岔过程。当ω=0.66时,系统表现为2/4周期振动,见图5a。当ω增大至0.667 2时,2/4周期振动发生擦边运动,见图5b。ω继续增大,系统在一个振动周期内的激振力周期数不变,但碰撞次数增加一次,2/4周期振动经实擦边分岔产生3/4周期振动,见图5c。当ω=0.668 26时,系统表现为6/8周期振动,见图5d。当ω=0.668 8时,系统表现为5/8周期振动,见图5e。系统在一个振动周期内的激振力周期数不变,但碰撞次数减少一次,因此,6/8周期振动经鞍结分岔产生5/8周期振动。当ω=0.668 95时,系统表现为10/16周期振动,见图5f。ω继续增大,系统经一系列实擦边分岔,周期倍化分岔和鞍结分岔最终变为复杂运动。
由图3a和图4b可以看出,在小l区域内,当ω增大时,2/4周期振动经虚擦边分岔直接跳变为复杂运动。图6清楚地显示了这一分岔过程。当ω=0.74时,系统表现为2/4周期振动,见图6a。当ω增至0.751 34时,2/4周期振动发生擦边运动,见图6b。ω继续增大,系统在一个振动周期内的激振力周期数和碰撞次数都发生了变化,2/4周期振动经虚擦边分岔直接转迁为复杂运动。2/4周期振动的虚擦边分岔过程是不可逆的,如图4c所示,当ω减小时,系统经3/4周期振动的逆周期倍化序列由复杂运动转迁为3/4周期振动。ω继续减小,3/4周期振动发生鞍结分岔产生2/4周期振动。
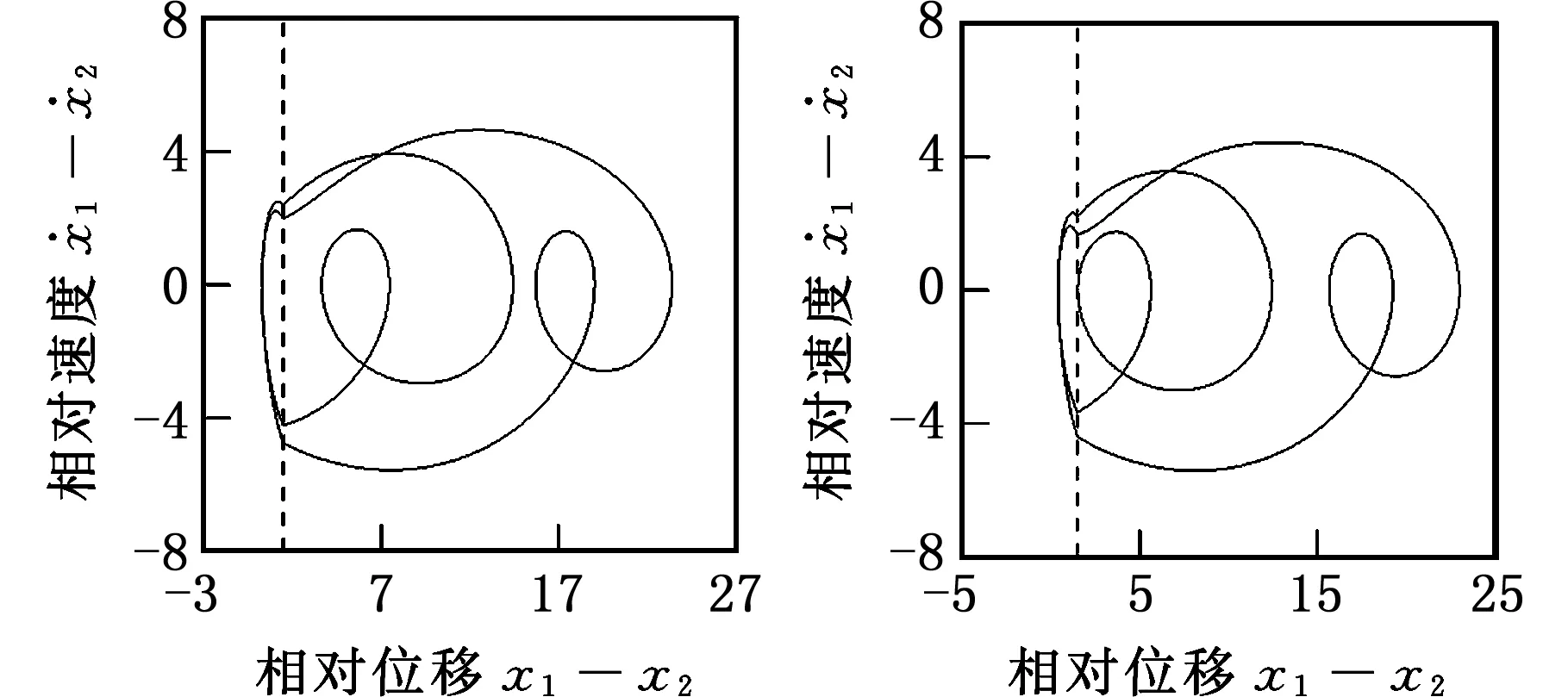
(a)2/4运动(ω=0.66)(b) 2/4擦边运动(ω=0.667 2)
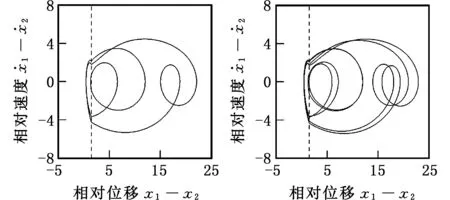
(c)3/4运动(ω=0.668)(d) 6/8运动(ω=0.668 26)
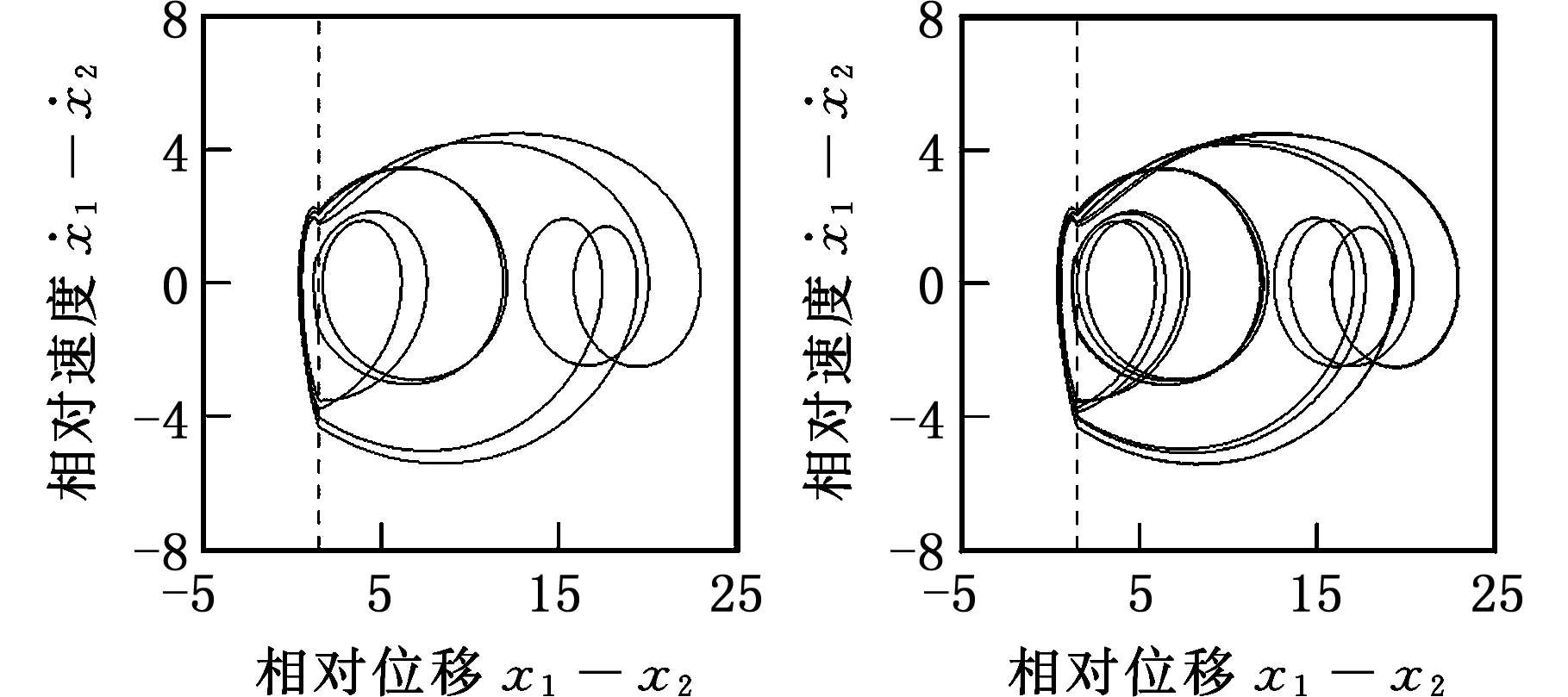
(e)5/8运动(ω=0.668 8)(f)10/16运动(ω=0.668 95)图5 相对运动的相图(l=1.5)Fig.5 Phase plane portraits of relative motion(l=1.5)
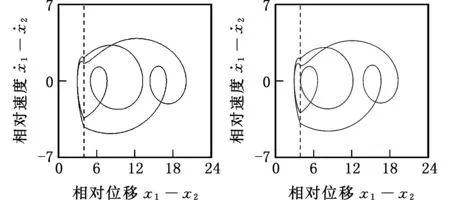
(a)2/4运动(ω=0.74)(b)2/4擦边运动(ω=0.751 34)图6 相对运动的相图(l=4.0)Fig.6 Phase plane portraits of relative motion(l=4.0)
由图3a和图4c可以看出,在大l区域内,当ω增大时,1/2亚谐振动经周期倍化分岔依次产生2/4、4/8和8/16周期振动,见图7a~图7c。ω继续增大,由于发生了8/16周期振动的实擦边分岔,使得1/2亚谐振动的周期倍化序列中断,产生9/16周期振动,见图7d~图7e。ω进一步增大,9/16周期振动依次发生周期倍化分岔,鞍结分岔和实擦边分岔,最终变为复杂运动。

(a)2/4运动(ω=0.87)(b) 4/8运动(ω=0.88)
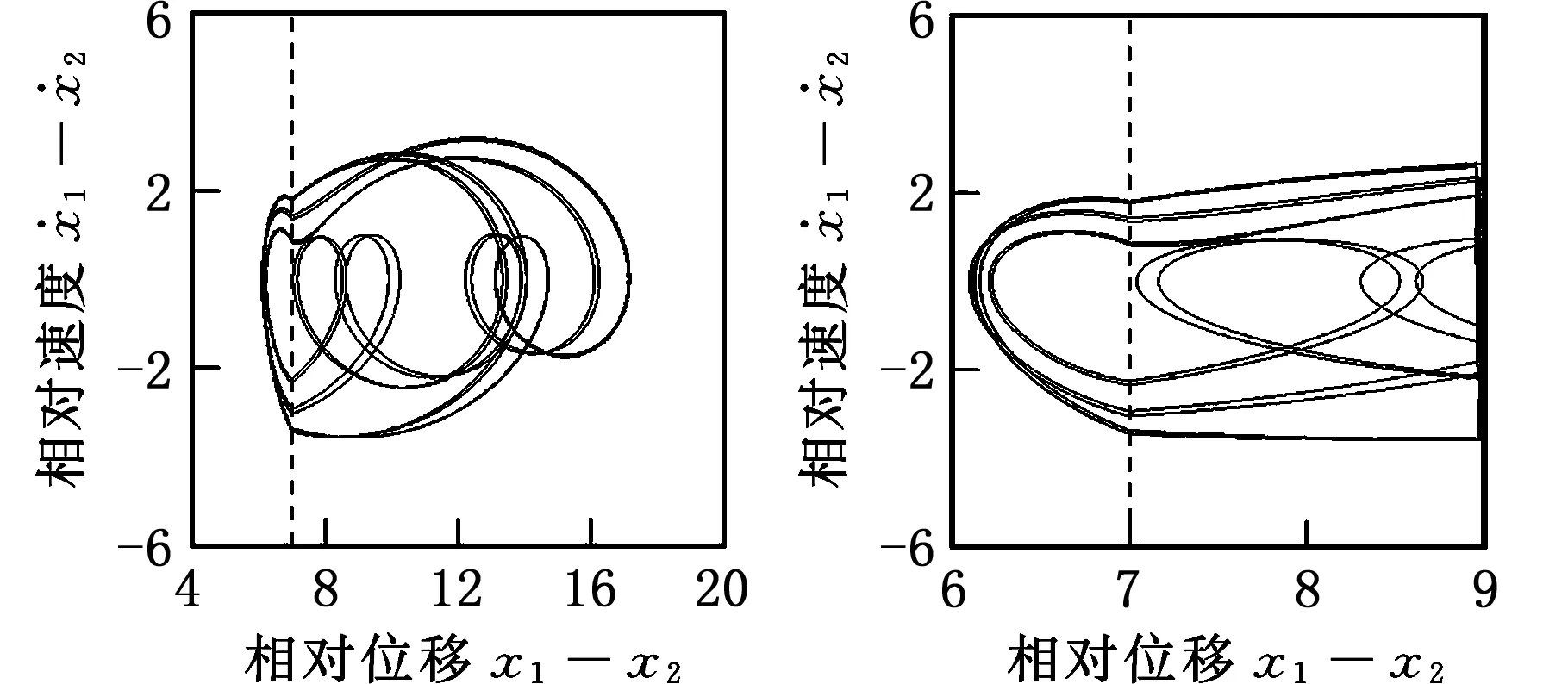
(c)8/16运动(ω=0.886)
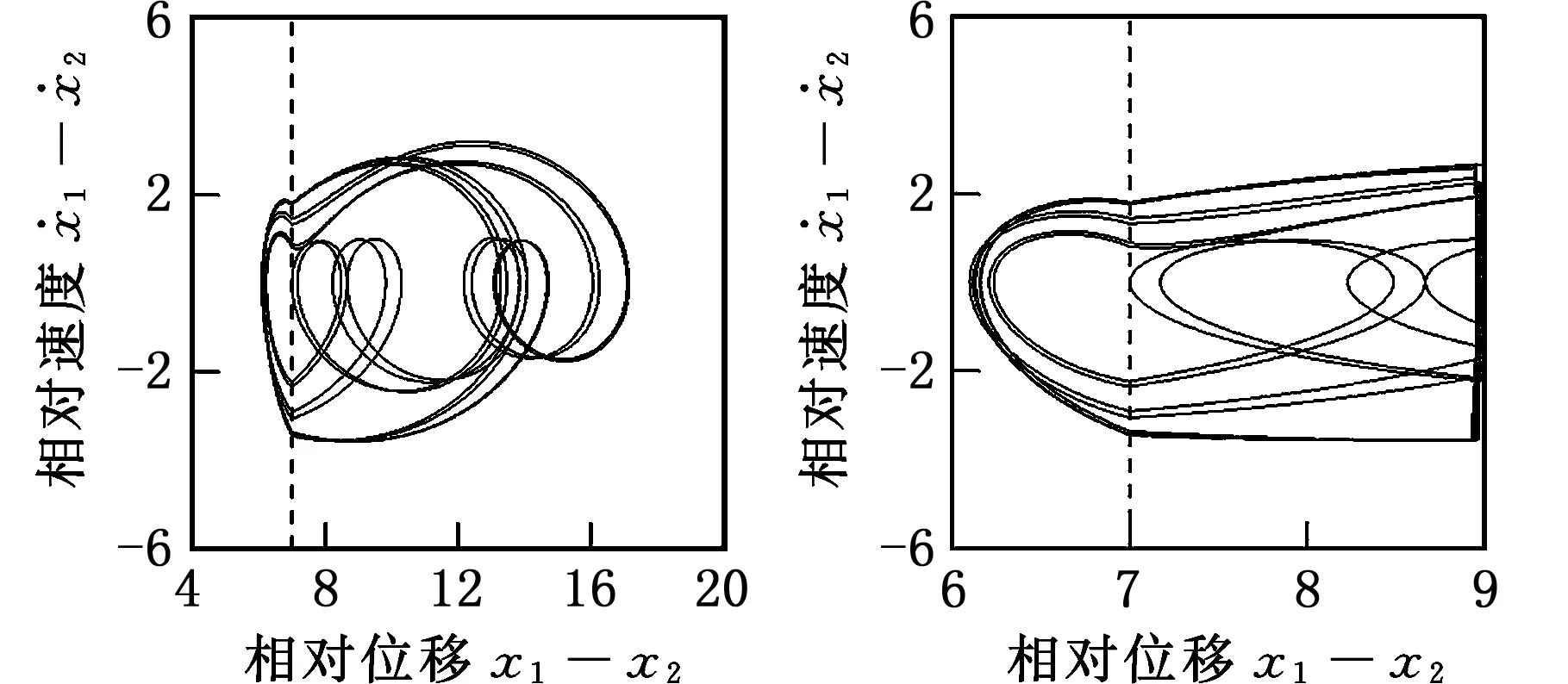
(d)8/16擦边运动(ω=0.886 5)

(e)9/16运动(ω=0.886 7)图7 相对运动的相图(l=7.0)Fig.7 Phase plane portraits of relative motion(l=7.0)
由图3b可以看出,1/3亚谐振动的分岔过程与1/2亚谐振动相似。由此可见,当ω增大时,在1/n亚谐振动向复杂运动的转迁过程中,倍化分岔普遍存在,但是由于实擦边分岔、虚擦边分岔或鞍结分岔等非光滑分岔的发生,使得其演化过程变得更加复杂,而且受预压量l值的影响比较大。
由图2、图3可见,在二维参数平面内,1/n(n≥1)周期振动和1/(n+1)亚谐振动的存在域之间存在2/(n+1)、4/(2n+2)、3/(2n+2)等周期振动的参数域,但系统主要呈现复杂运动。l增大,复杂运动的激振频率窗口明显增大。
为了研究周期振动的类型、冲击速度和滑块渐进率三者之间的关联关系,图8给出了激振器的冲击速度和滑块在有限时间内(t=200)的渐进量在二维参数(ω,l)平面上的分布图。图8中,单碰周期振动的响应和其余类型振动的响应用不同颜色线型来表示,各类周期振动的参数域在(ω,l)-参数平面内的分布如图2所示。由图2、图8可见,激振器冲击缓冲垫的速度越大,滑块的渐进率越好。1/1周期振动的冲击速度和渐进量要明显大于其他类型周期振动的冲击速度和渐进量。因此,实际工程应用的最佳选择应该是使系统工作于1/1周期振动的冲击速度峰值附近,以获取较好的渐进效果。
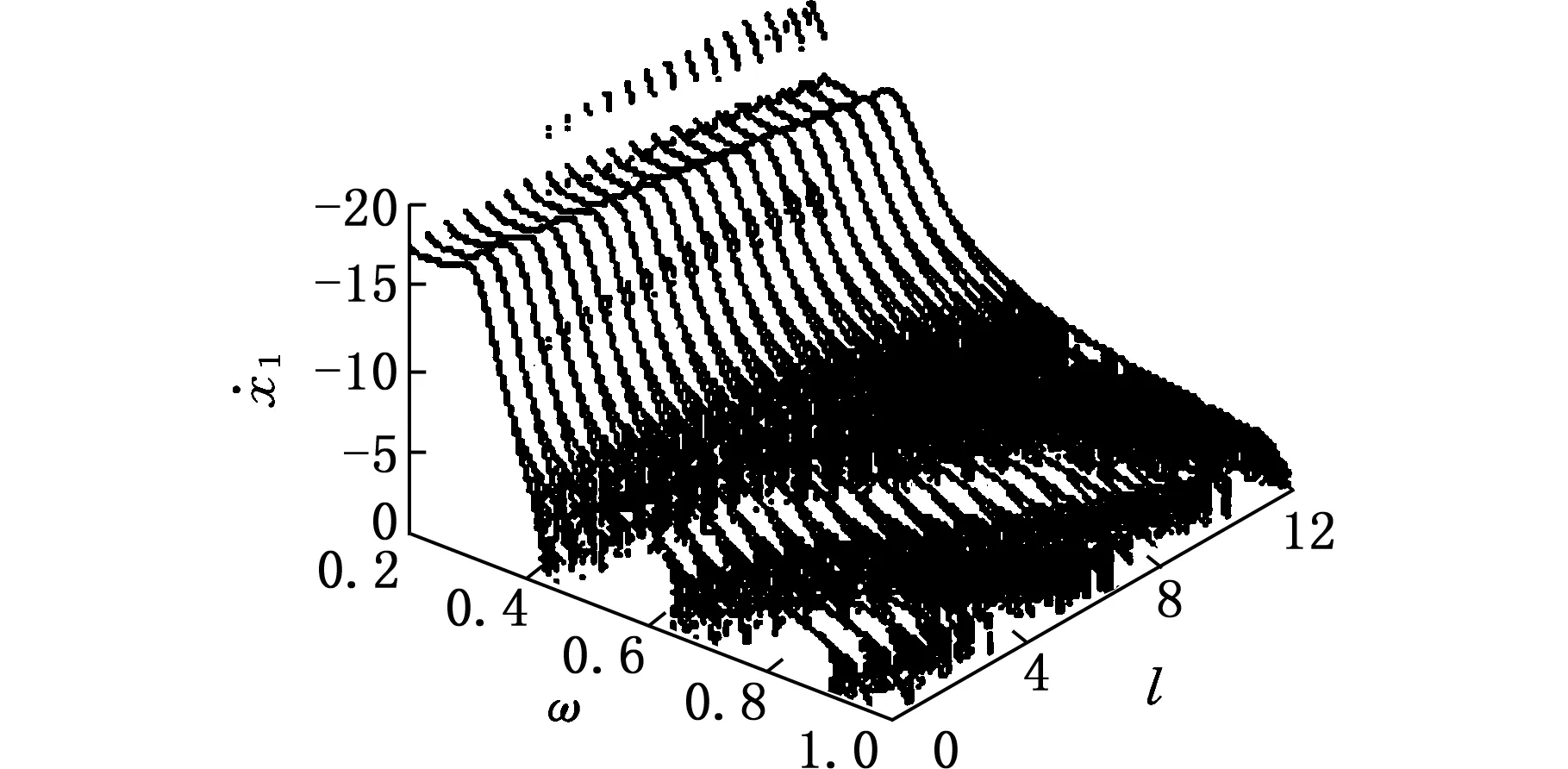
(a)冲击速度分布图

(b)滑块在有限时间内的渐进量分布图图8 二维参数平面分布图Fig.8 Distribution diagram in two-dimensional parameter plane
4 结论
(1)在二维参数平面内,系统主要呈现1/n单碰周期振动。预压量l对1/1周期振动的分岔过程没有影响,但l对1/n亚谐振动的分岔过程的影响比较大。
由于汉语和英语具有不同的语调特点,而英语的语调又十分复杂多变,所以有些中国学生尽管能发出正确的英语语音,但仍然不能用地道的语调和节奏读出英语句子。为此,教学时可以通过揭示以下规律帮助学生学习英语语音。
(2)当ω增大时,1/n亚谐振动发生周期倍化分岔,产生2/2n周期振动。ω继续增大时,由于周期振动的实擦边分岔、虚擦边分岔或鞍结分岔等非光滑分岔的发生,使得1/n亚谐振动的分岔过程变得更加复杂。
(3)研究结果表明,激振器冲击缓冲垫的速度越大,滑块的渐进率越好。1/1周期振动的冲击速度和渐进量要明显大于其他类型周期振动的冲击速度和渐进量。在设计和改造碰撞-渐进类机械设备时,通过多参数协同仿真分析可以确定动力学参数的合理匹配规律,有利于使系统在较大的参数区域内呈现稳定的1/1周期振动,从而获得较大的瞬时冲击速度和较好的渐进效果。
(4)研究结果对工程实际中碰撞-渐进类机械设备的设计及其参数的优化选择具有理论指导意义。
[1] 秦志英, 李群宏. 一类非光滑映射的边界碰撞分岔[J].力学学报, 2013, 45(1): 25-29.
QIN Zhiying, LI Qunhong. Border-collision Bifurcation in a Kind of Non-smooth Maps [J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(1): 25-29.
[2] 刘莉, 徐伟, 岳晓乐,等. 一类含非黏滞阻尼的Duffing单边碰撞系统的激变研究 [J]. 物理学报, 2013, 62(20): 60-67.
LIU Li, XU Wei, YUE Xiaole,et al. Global Analysis of Crises in a Duffing Vibro-impact Oscillator with Non-viscously Damping [J]. Acta Phys. Sin., 2013, 62(20): 60-67.
[3] 冯进钤. 单边碰撞系统的擦边诱导鞍结分岔 [J]. 安徽大学学报, 2011, 35(5): 22-25.
FENG Jinqian. Grazing-induced Saddle-node Bifurcation in a Unilateral Vibro-impact System [J]. Journal of Anhui University, 2011, 35(5): 22-25.
[4] 王强, 汪少铭, 刘永葆,等. 阻尼对三自由度弹性碰撞系统周期运动倍化分岔的影响研究 [J]. 武汉理工大学学报(交通科学与工程版),2015, 39(6): 1249-1254.
WANG Qiang, WANG Shaoming, LIU Yongbao,et al. Period-doubling Bifurcation of Three-degree-of-freedom Elastic Collision System under Different Damping Coefficient [J].Journal of Wuhan University of Technology (Transportation Science and Engineering),2015,39(6): 1249-1254.
[5] PETERKA F, BLAZEJCZYK-OKOLEWSKA B. Some Aspects of the Dynamical Behavior of the Impact Damper [J]. Journal of Vibration and Control, 2005, 11(4): 459-479.
[6] HUMPHRIES N, PIIROINEN P T. A Discontinuity-geometry View of the Relationship between Saddle-node and Grazing Bifurcations [J]. Physica D, 2012, 241(22): 1911-1918.
[7] 李晟,吴庆鸣,张志强,等. 两级行星轮系分岔与混沌特性研究 [J]. 中国机械工程, 2014, 25(7): 931-937.
LI Sheng, WU Qingming, ZHANG Zhiqiang,et al. Bifurcation and Chaos Characteristics of Two-stage Planetary Gear Train Sets [J]. China Mechanical Engineering, 2014, 25(7): 931-937.
[8] 黑棣, 吕延军, 张永芳. 有限长轴承支撑的转子系统非线性动力学分析 [J]. 中国机械工程, 2015, 26(19): 2633-2640.
HEI Di, LYU Yanjun, ZHANG Yongfang. Analysis of Nonlinear Dynamics of Rotor System Supported by Finite Long Bearing [J].China Mechanical Engineering, 2015, 26(19): 2633-2640.
[9] PAVLOVSKAIA E, HENDRY D C, WIERCIGROCH M. Modelling of High Frequency Vibro-impact Drilling [J]. International Journal of Mechanical Sciences, 2015, 91(2): 110-119.
