优化参数的变分模态分解在滚动轴承故障诊断中的应用
2018-03-06马洪斌佟庆彬张亚男
马洪斌 佟庆彬 张亚男
北京交通大学电气工程学院,北京,100044
0 引言
滚动轴承在运行过程中容易发生故障,若能在早期准确地判断是否发生故障,并能准确地判断故障发生的类型,对系统的运行具有重要意义。滚动轴承发生故障时,振动波形中会出现周期性脉冲信号[1],但是由于波形比较复杂,难以提取出其中的特征信息。
经验模态分解(empirical mode decomposition, EMD)是一种自适应的分解方法,已得到机械故障诊断领域相关学者的认可和广泛的关注。文献[2-4]将EMD分解应用到滚动轴承故障特征提取中,获得了较好的效果。但是由于EMD分解采用了极值点的包络求取方法,包络估计误差经多次递归分解被放大,易出现模态混叠的现象。
2014年DRAGOMIRETSKIY等[5]提出了一种新的自适应信号处理方法——变分模态分解(variational modal decomposition,VMD),该方法通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,能够实现信号的频域剖分及各个变量的有效分离。但是VMD分解时需要考虑惩罚项参数和分解个数的影响,因此,本文利用蛙跳算法对参数优化,对模态函数进行包络分析,与实际的故障频率相比较,从而验证所得的参数为最优参数,再利用奇异值分解[6]对模态函数构成的矩阵进行分解,得到信号的奇异值。奇异值是矩阵的固有特性,具有很好的稳定性、比例不变性和旋转不变性,可以有效地刻画出初始特征向量矩阵的特性。最后利用极限学习机(extreme learning machine,ELM)[7]对故障类型进行模式识别,其学习速度快,且泛化性能好。
政策一:4月20日,商务部办公厅发布《关于做好2018年绿色循环消费有关工作的通知》。《通知》提出,2018年,商务部将在绿色商场开展塑料购物袋减量工作,大力倡导绿色商场减少塑料袋使用,引导绿色商场加大“减塑”力度,加快绿色包装标准化进程。
1 变分模态分解
1.1 变分问题的构造
变分问题是搜寻k个本征模态函数uk(t),使每个模态的估计带宽之和最小,约束条件为所有模态之和等于输入信号[8]。
1.2 变分问题的求解
本节实验中,假设采样率定义为α=M′/M,其中M′为重构利用的量测值个数,M为所有的量测值个数;重构误差计算公式为式中x为原信号,为重构结果;信噪比添加方式同文献[10].由于本文方法在方位向重构时利用了联合稀疏特征,因此本节首先分析方位向基于联合稀疏模型的重构性能,再进行二维成像性能分析.
(3)将本征模态函数分量中包络熵最小的分量(即与局部极小熵值对应的模态分量)作为最佳分量,进行包络分析。
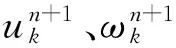
从长远来看,我国应尽力去教育和训练专门从事环境会计的职业人才,在大中专学校增添环境会计、审计专业课,为用人单位栽培具有权利和行为能力的工作人员。企业应培养和训练相应的会计人员,使得符合环境会计的要求,使会计人员的思想与行为得到很好的表现,可以设立定期的考核制度,保证企业内部员工的综合表现符合企业的要求,为企业的发展贡献一份力量。增强财会人员与环境技术人员、生产员工等的沟通,彼此了解对方的知识和必要信息,寻找适合的环境会计信息披露计量方法和披露形式。[17]相关环境会计人员理应学习和熟悉相关环境会计专业知识,这样对于环境会计实践工作的顺利开展有很大的益处。
(3)利用在范数下的Parseval/Plancherel等距傅里叶变换,问题可以在频域范围内解决。
同理,将中心频率的取值问题转化到频域,得到中心频率的更新。
1.3 VMD算法
VMD算法是将各个模态直接在频域范围内不断地更新,最后通过傅里叶逆变换变换到时域范围中,算法步骤详见文献[8]。
(2)利用蛙跳算法对VMD参数优化,结果得到一组优化的全局最优解[ko,αo],将VMD的分解个数和二次惩罚项系数分别设定为ko和αo,对故障信号进行分解,得到一系列本征模态函数。
2 基于蛙跳算法优化的变分模态分解
VMD算法与EMD算法的一个较大区别是,使用VMD算法处理信号时,需要预先设定所得到的本征模态函数的个数k和二次惩罚项系数α,设置不同的k和α,信号处理的结果大大不同。VMD算法中的α对信号处理结果的影响体现在:α越小,所得的k个模态函数的带宽越大;反之,α越大,所得的k个模态函数的带宽越小。通常情况下k和α的选取难以确定,需要一种优化的算法即基于蛙跳算法的变分模态分解进行参数的选取。
蛙跳算法具有概念简单、调整的参数少、计算速度快、全局搜索寻优能力强、易于实现的特点,因此,利用蛙跳算法对变分模态分解的参数进行优化,可以避免人为主观因素带来的影响,自动筛选出最佳影响参数[9]。
利用蛙跳算法进行参数优化时,需要一个适应度函数[10]。每次更新需要计算一次适应度值,通过比较适应度值进行更新。定义信号的包络熵:
(1)
式中,a(i)为信号x(i)经过Hilbert解调后的包络信号;pi为a(i)的归一化形式。
由以上包络熵的表达式可以看出,包络熵反映了信号的稀疏特性。信号稀疏性越强,包络熵越小;反之,信号稀疏性越弱,包络熵越大[11]。滚动轴承早期故障信号经VMD处理后,若得到的本征模态函数分量中包含的噪声较多,故障周期性特征分量不明显,则信号稀疏性较弱,包络熵较大;若分量中故障特征信息多,波形中出现规律性周期脉冲,则信号的稀疏性较强,信号的包络熵较小。当某一组参数(k,α)确定时,经过VMD分解得到的所有的包络熵中,将最小的一个称为局部极小熵值,该组分量为含有故障特征信息的最佳分量。为了获得全局最优值,以局部极小熵值作为适应度值,以局部最小熵值最小化作为寻优目标,利用蛙跳算法对变分模态分解参数进行优化。
蛙跳算法寻优及故障模式识别的步骤如下:
对于容易解决的问题情境,如:利用简单问题创设的问题情境,学生通过自己阅读教材,积极思考就可以解决,就放手让学生独立去解决。
其中,s(t)为周期脉冲冲击信号,模拟故障产生的冲击信号;n(t)为高斯白噪声信号;Ai为幅值调节系数;h(t)为幅值衰减的振荡信号;衰减系数C=700;共振频率fn=3 kHz;幅值初值A0=0.3;转频fr=20 Hz。人为设置的模拟故障频率fi=1/T=80 Hz;采样频率fs=12 kHz。
PInvit=a0+a1Epuit+a2Ffriit×I(Ffriit≤ρ)+a3Ffriit×I(Ffriit>ρ)+a4Epuit×Irrit
3)在不同温度、相同的空气湿度中,温度越高,金银花的平衡含水率越低。从测得的3条曲线来看,温度对金银花平衡含水率的影响并不太大,因此决定金银花贮藏性能的主要因素是空气的相对湿度。
(4)将包络谱中故障特征频率值与轴承故障理论值进行比较,判断故障。
(5)将VMD分解获得的模态函数构成矩阵形式,对矩阵进行奇异值分解,获得故障信号的特征向量。
(1)通过引入二次惩罚项系数α和拉格朗日乘法算子λ(t),将约束性变分问题转化成非约束性变分问题。
(6)以特征向量作为极限学习机的输入,对故障类型进行识别,并与神经网络(BP)、支持向量机(SVM)、交叉验证的支持向量机(Cg-SVM)、粒子群优化的最小支持向量机(PSO-LSSVM)识别结果做比较。
3 仿真信号分析
为了验证基于蛙跳算法优化参数的变分模态分解的有效性,利用故障仿真信号进行模拟实验。仿真信号主要由故障模型模拟轴承故障产生的冲击信号和噪声信号组成[12]。仿真信号的表达式如下:
为了说明该方法的优势,利用EMD分解对信号进行处理,得到一系列模态函数分量,由于EMD分解得到的模态分量太多,故只取包含特征频率的部分,选择最佳的分量作包络分析。图5所示为EMD分解得到的前4个模态分量及各自的频谱。选择最佳的模态分量IMF1作包络解调分析,图6为IMF1的包络谱。
x(t)=s(t)+n(t)
(9)
Ai=1+A0sin(2πfrt)
h(t)=e-Ctsin(2πfnt)
(1)对蛙跳算法的各参数进行设定。种群组数m=10,每组青蛙个数n=10,组内迭代数Ne=10,种群总进化代数(MAXGEN)为10。
图1为仿真信号的波形图和包络谱图,冲击信号淹没在噪声信号中,无法发现信号频率和周期,从包络谱图中也无法准确地找到故障的特征频率。
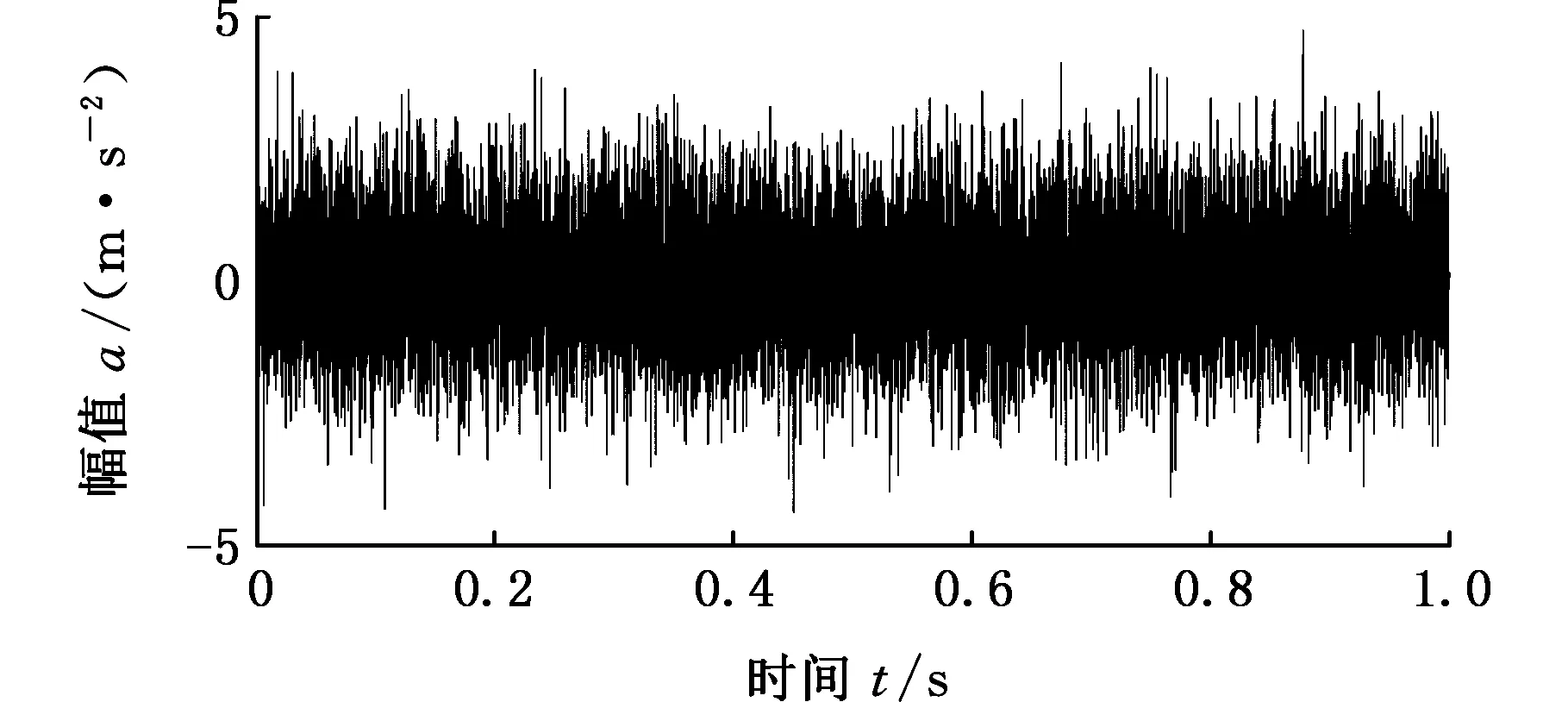
(a)故障仿真信号图
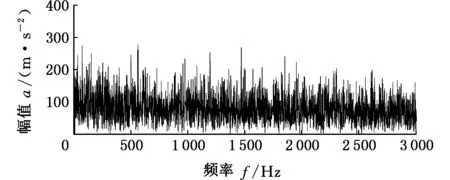
(b)故障仿真信号包络谱图1 故障仿真信号及其包络谱Fig.1 Signal diagram and envelope spectrum of fault simulation signal
采用蛙跳算法对VMD参数进行优化,如图2所示,可以看出局部极小熵值1.58出现在第13代上,局部极小熵值所对应的组合最佳参数为[6,3 000]。设置VMD分解参数对信号进行分解,得到6个本征模态分量IMF1~IMF6,波形与所对应的频谱如图3所示。其中,最小包络熵所对应的模态分量是IMF5,选其为最佳分量,进一步做包络分析,得到信号的包络谱如图4所示。可以看出,在特征频率f及特征频率的倍频处频谱幅值突出,说明通过该方法可以正确地分解故障信号并准确提取出故障信号的特征频率。
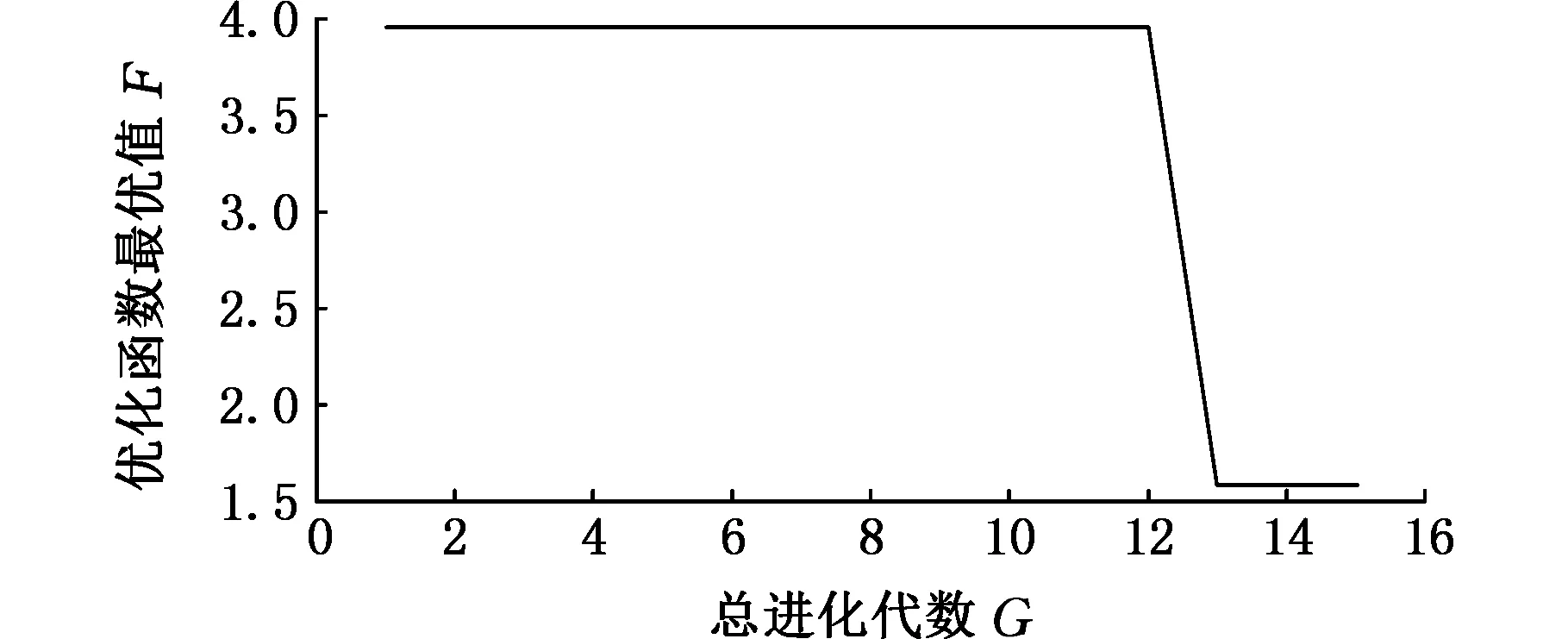
图2 蛙跳算法优化值随进化代数的变化曲线(仿真)Fig.2 The optimized value curve leapfrog algorithm with the evolution algebra(simulation)
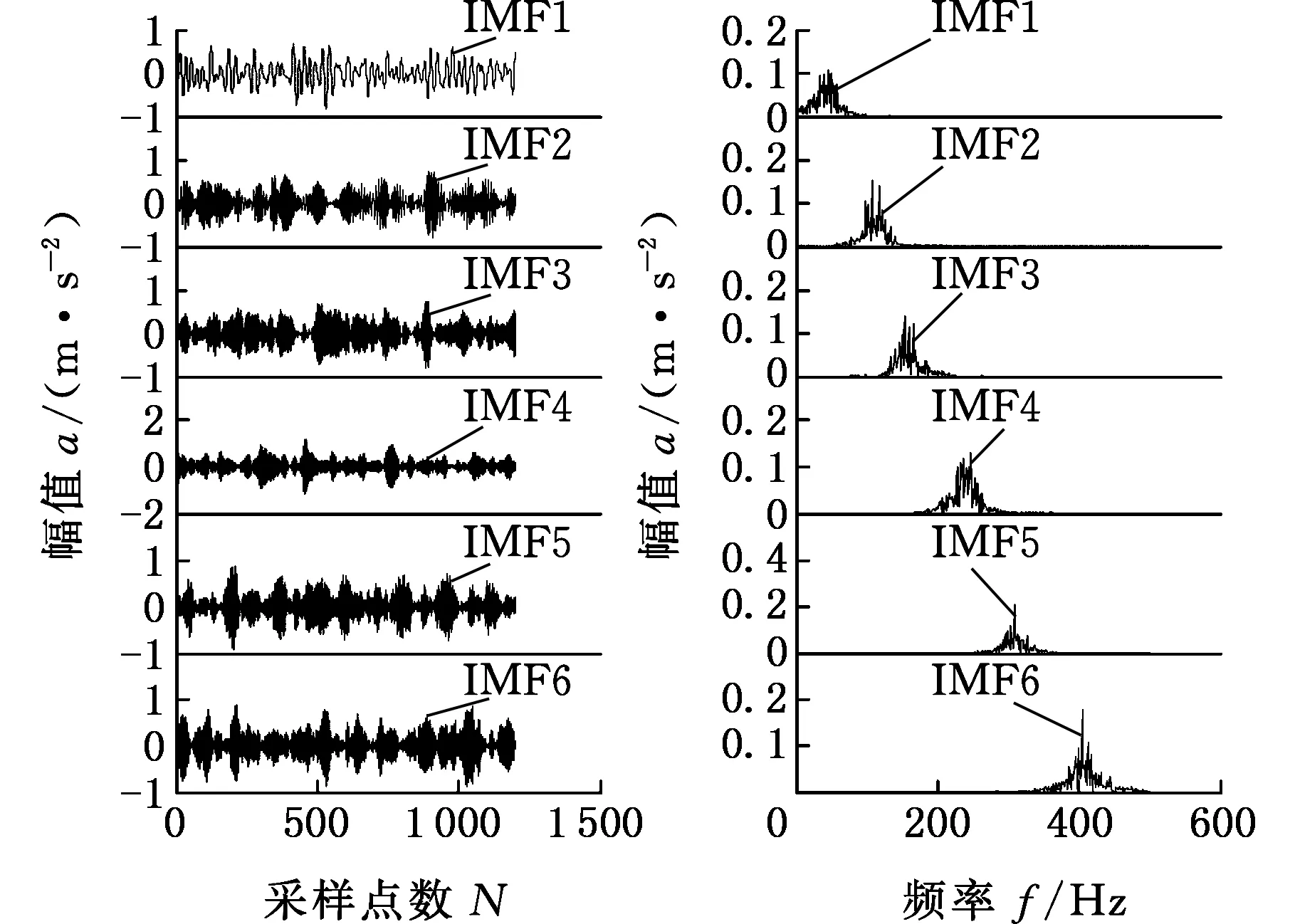
(a)波形 (b)频谱图3 VMD分解得到的模态函数及频谱Fig.3 Modal function and spectrum of VMD
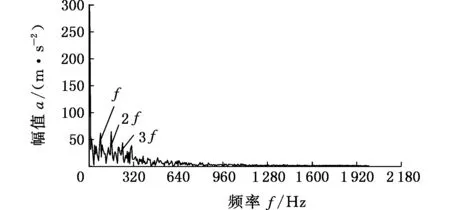
图4 VMD最佳分量包络谱Fig.4 Envelope spectrum of the best mode function of VMD
第二,建筑类专业英语课程的设置需要以就业为前提,不仅要为学生传授理论知识,还要不断加强学生的实践能力,教师需要多与建筑企业沟通,了解企业需要的哪方面的人才,及时调整教学计划与教学内容。
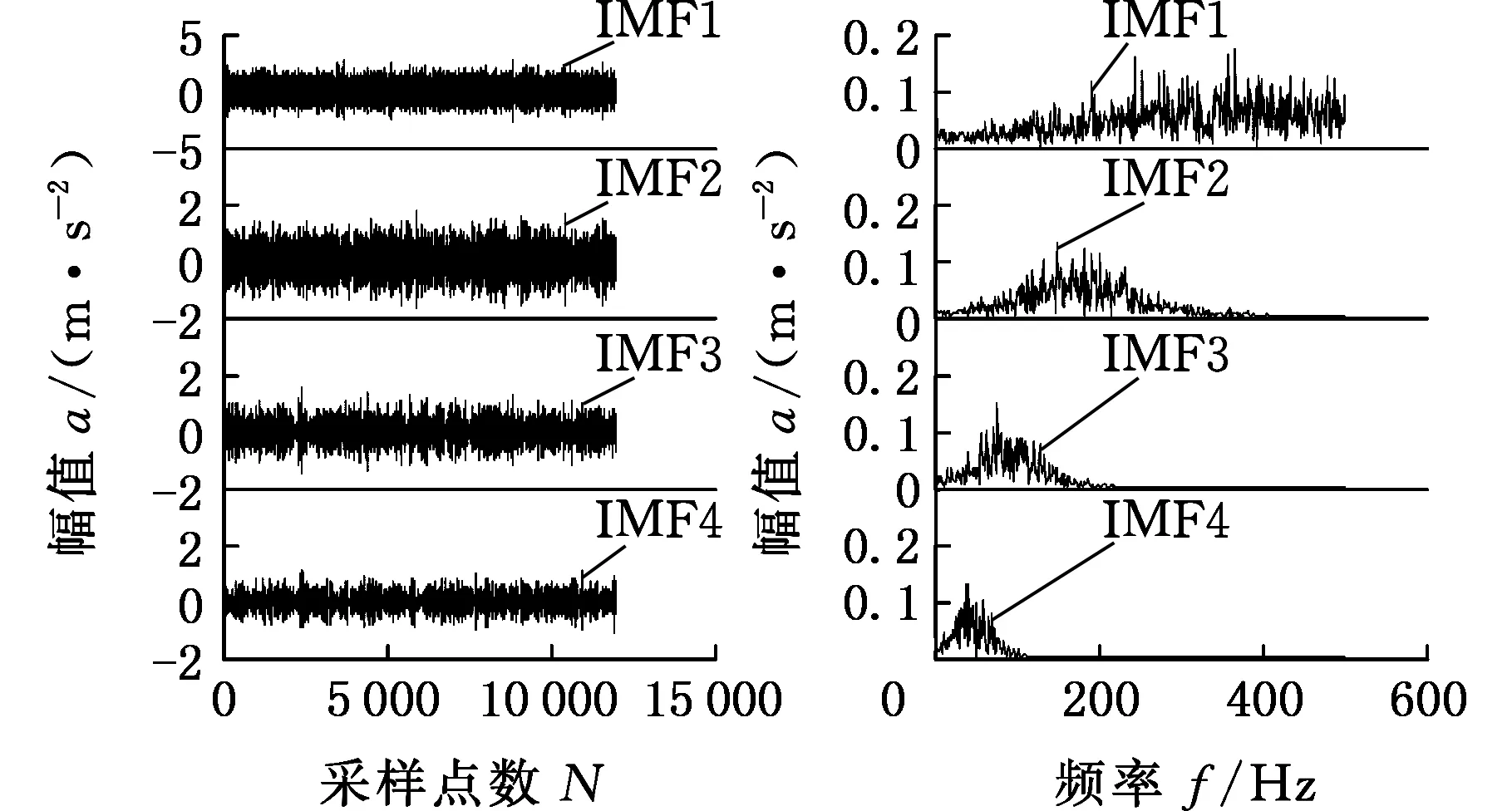
(a)波形 (b)频谱图5 EMD分解得到的模态函数及频谱Fig.5 Modal function and spectrum of EMD
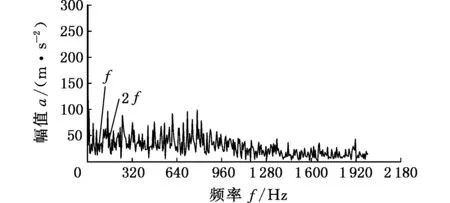
图6 EMD最佳分量包络谱Fig.6 Envelope spectrum of the best mode function of EMD
首先从两种分解方法获得的分量的波形图上可以看出,EMD分解获得的分量存在模态混叠的现象,对分量作包络谱分析,除特征频率之外还有其他频率,并且特征频率不是十分突出,难以从一系列频率中发现特征频率;而基于蛙跳算法获得最佳参数的VMD分解可以正确有效地提取出模态函数中最佳分量,且分量的包络谱中特征频率十分突出。故VMD相对于EMD而言,特征频率更加明显。
4 实测信号分析
将该方法用于实际的故障信号以验证其可靠性。试验台由2马力(1 470.997 5 W)的感应电动机、转矩传感器和功率计组成,驱动端轴承为6205-2RS JEM SKF深沟球轴承。轴承的故障是通过放电加工技术得到的。故障的直径为0.177 8 mm(0.007英寸),滚动轴承功率为0时,轴承的转速为1 797 r/min;滚动轴承在1马力(735.498 75 W)时,轴承的转速为1 772 r/min。采样频率为12 kHz,用加速度传感器获得外圈故障、内圈故障和滚动体故障的振动信号。轴承的内圈直径为25.001 22 mm(0.984 3英寸),外圈直径为51.998 88 mm(2.047 2英寸),厚度为15.001 24 mm(0.590 6英寸),滚动体直径为7.940 04 mm(0.3126英寸),滚动体节径(即轴承节径)为39.039 8 mm(1.537英寸),钢球数为9,滚动体接触角α为90°。经计算可得到滚动轴承外圈故障的特征频率为107.4 Hz,内圈故障特征频率为160 Hz,滚动体单故障特征频率为69 Hz[13]。
4.1 外圈故障分析
图7为滚动轴承外圈故障信号的波形图和包络谱图。由信号的包络谱可看出,除突出的频率之外,还包含其他的频率,容易对故障误判。
参数设置时可以输入待检查报文名称中含有的关键字符,如日数据的到报检查可以输入关键字符“DAY”。并输入多个关键字符,用“,”隔开,如图4。软件通过参数设置的关键字符检查报文的到报情况,确认上传目录里是否有最新的报文。这样可以避免之前很多软件只能进行一种报文检查的局限性。观测员通过参数设置可以设置检查任何需要上传的报文,除常规站的长Z文件,也包括酸雨、风廓线、大气成分等其他的传输文件。
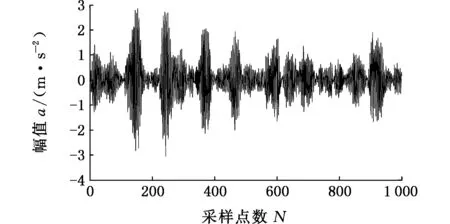
(a)滚动轴承外圈故障波形
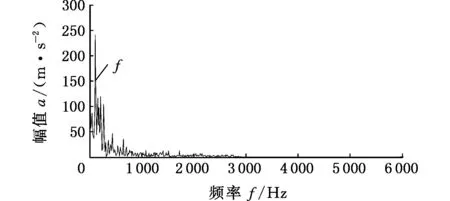
(b)外圈故障信号包络谱图7 滚动轴承外圈故障波形图及信号包络谱Fig.7 Waveform diagram and signal envelope spectrum of outer ring fault of rolling bearing
采用蛙跳算法对VMD参数进行优化,如图8所示,可以看出群体进化到第10代时得到了局部极小熵值-1.497,对应的最佳组合参数为[6,2 000],进行VMD分解得到6个模态函数分量,其中,最佳模态函数分量与频谱如图9所示,对最佳分量进行包络分析,得到信号的包络谱如图10所示。
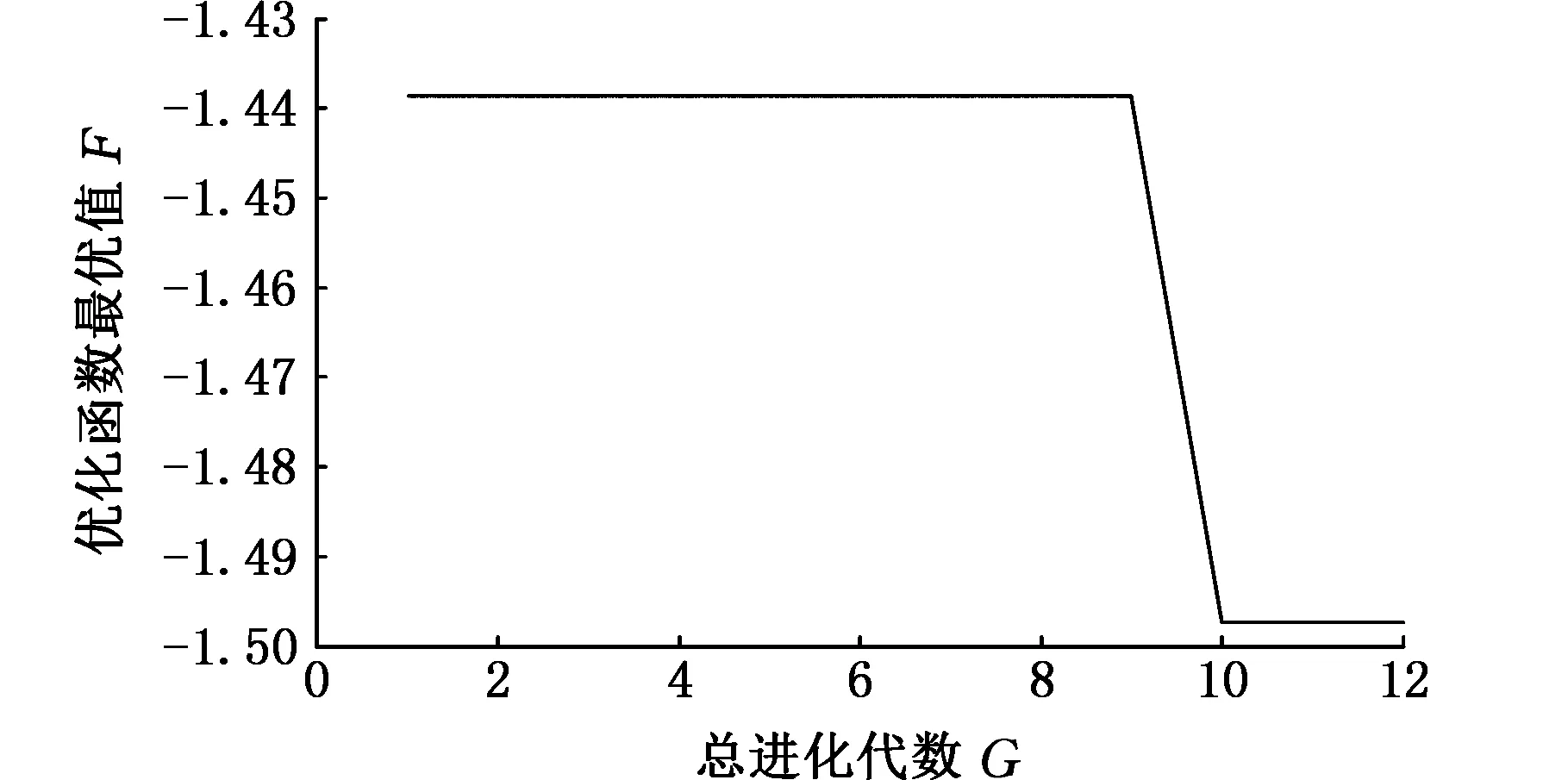
图8 蛙跳算法优化值随进化代数的变化曲线(外圈故障)Fig.8 The optimized value curve leapfrog algorithm with the evolution algebra(outer ring fault)
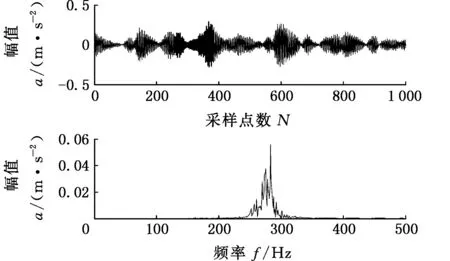
图9 VMD分解得到的最佳模态函数及频谱(外圈故障)Fig.9 The best modal function and spectrum of the VMD decomposition(outer ring fault)
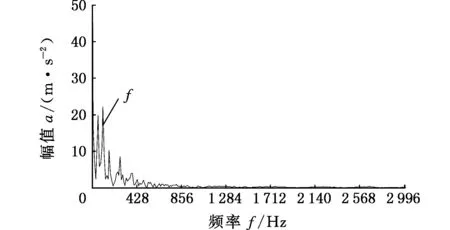
图10 VMD最佳模态函数包络谱(外圈故障)Fig.10 Envelope spectrum of the best mode of VMD(outer ring fault)
同理,利用EMD对滚动轴承故障信号进行处理,得到各个模态函数,图11和图12所示分别为经过EMD分解之后得到的各模态函数中的最佳分量及其包络谱。
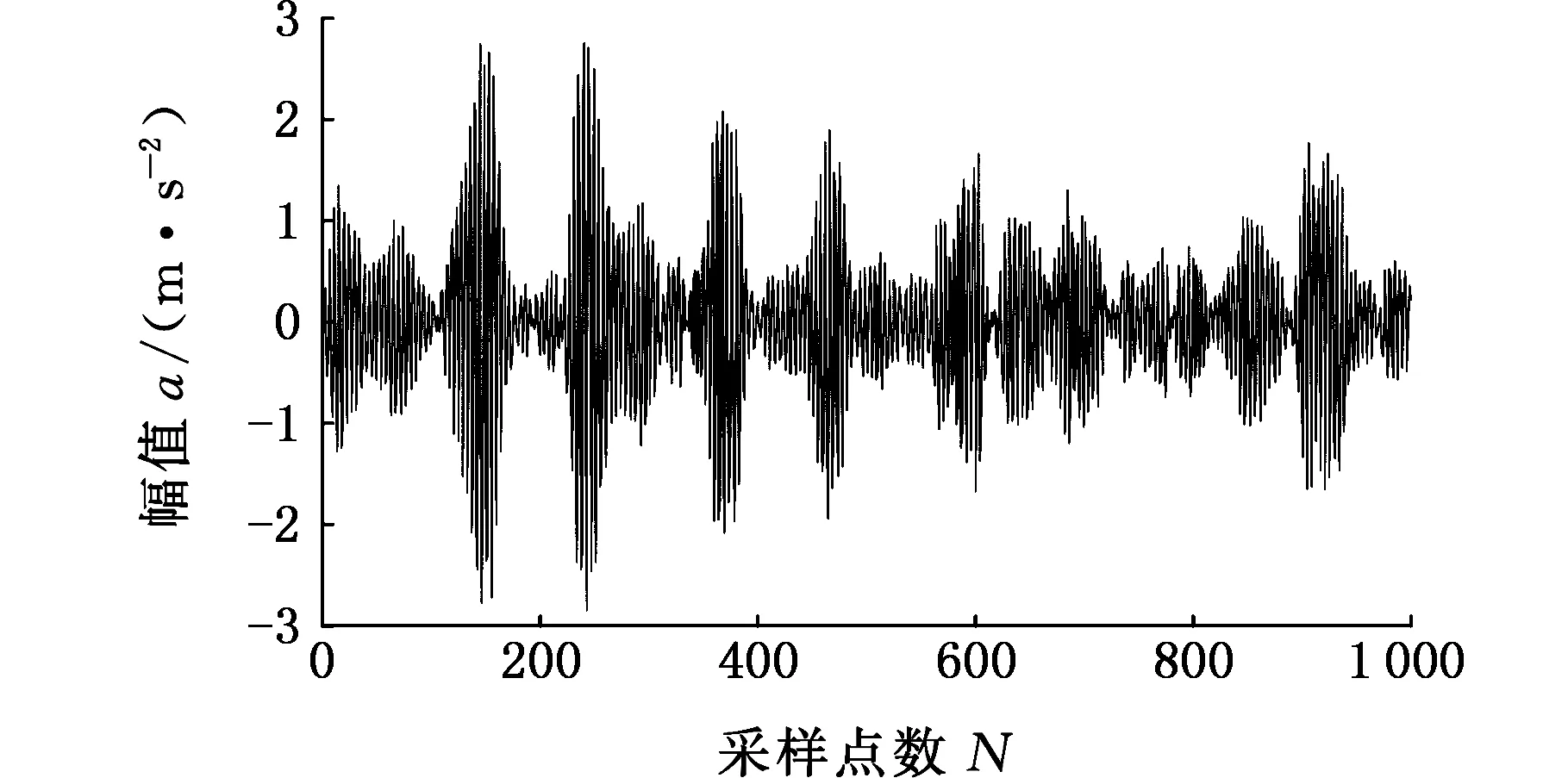
图11 EMD分解得到的最佳模态分量(外圈故障)Fig.11 Optimal modal component of EMD(outer ring fault)

图12 EMD最佳分量包络谱(外圈故障)Fig.12 Envelope spectrum of the best mode of EMD (outer ring fault)
4.2 内圈故障分析
图13为滚动轴承内圈故障信号的波形图和包络谱图。采用蛙跳算法对VMD参数进行优化得到局部极小熵值的变化曲线,如图14所示,可以看出,群体进化到第10代时得到了局部极小熵值-6.13,对应的最佳组合参数为[7,2 000],以得到优化参数的VMD对内圈故障信号进行处理,得到7个模态函数分量,其中,最佳模态函数的波形图与频谱图见图15。对最佳模态函数进行包络分析,得到信号的包络谱如图16所示。
本文基于空气源热泵与燃气锅炉耦合供热项目,在TRNSYS平台上搭建空气源热泵与燃气锅炉耦合供热系统瞬态计算模型,针对青岛市气象条件和价格体系,找到了耦合供热系统的运行费用平衡点.在此基础上,以耦合供热系统的最低费用年值为目标,得到空气源热泵承担的最佳设计负荷,充分发挥空气源热泵运行费用低、燃气锅炉供热稳定的优点,对相关项目的实施具有一定的指导意义.
过了几天,班上最喜欢打小报告的孩子神秘兮兮地跑来跟我说:“老师,班上的同学都说班长有女朋友了。”联想到我在露露空间里看到的文字,这件事我得关注了。再次翻看手机,却发现好几个孩子的空间里都有关于小雨和梓轩的议论。作为班主任,我该怎么办?

(a)滚动轴承内圈故障信号波形图
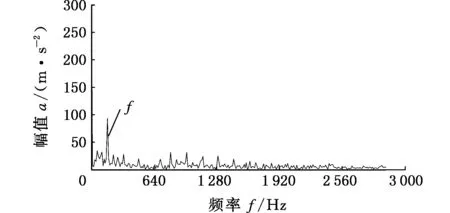
(b)内圈故障信号包络谱图13 滚动轴承内圈故障信号波形图及包络谱Fig.13 Waveform diagram and envelope spectrum of inner ring fault signal of rolling bearing
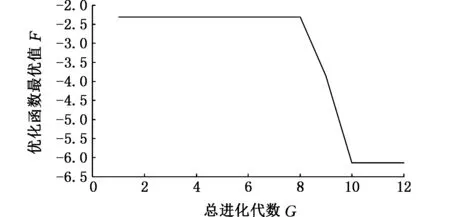
图14 蛙跳算法优化值随进化代数的变化曲线(内圈故障)Fig.14 The optimized value curve leapfrog algorithmwith the evolution algebra(inner ring fault)
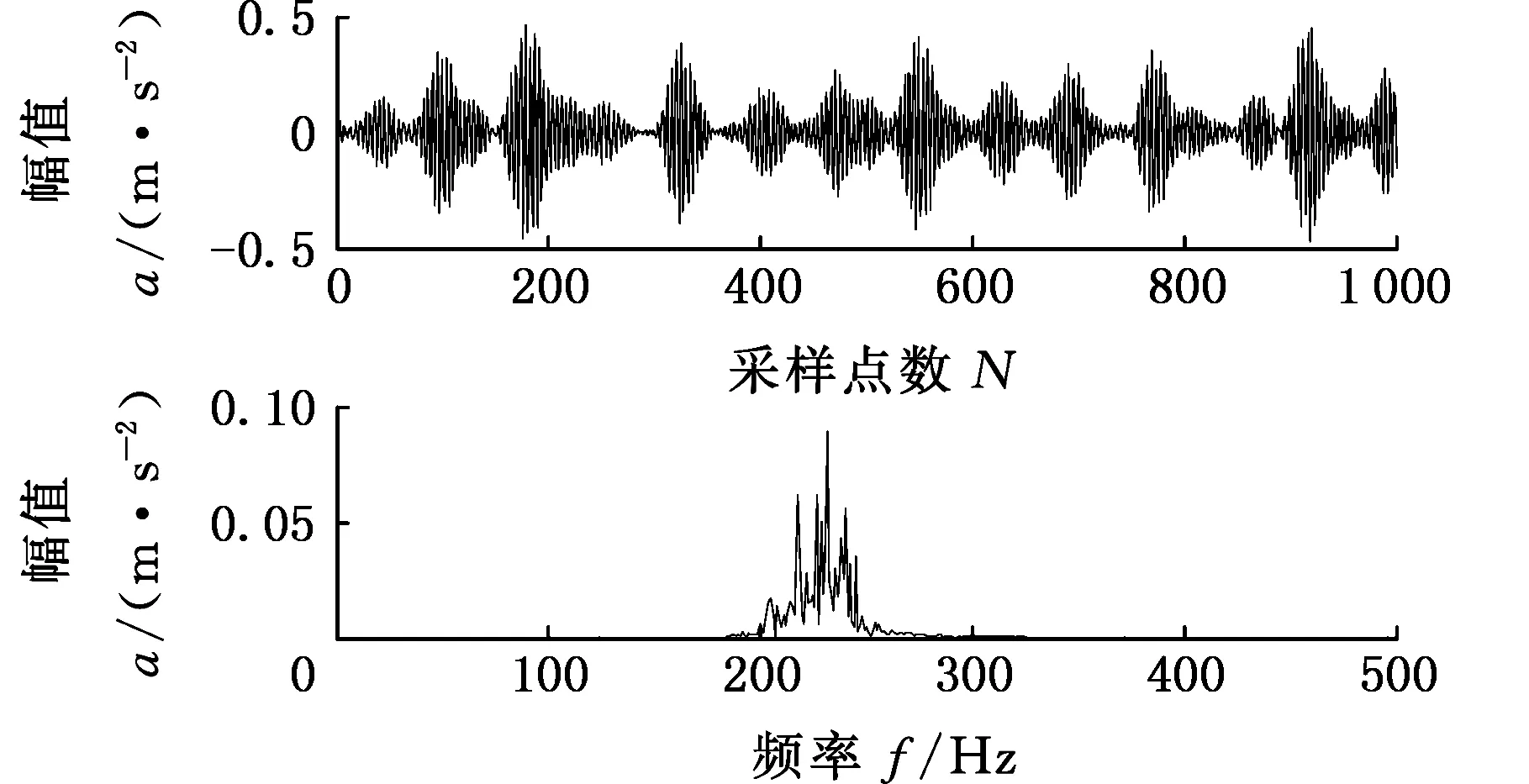
图15 VMD分解得到最佳模态函数及频谱(内圈故障)Fig.15 The best modal function and spectrum of the VMD decomposition(inner ring fault)
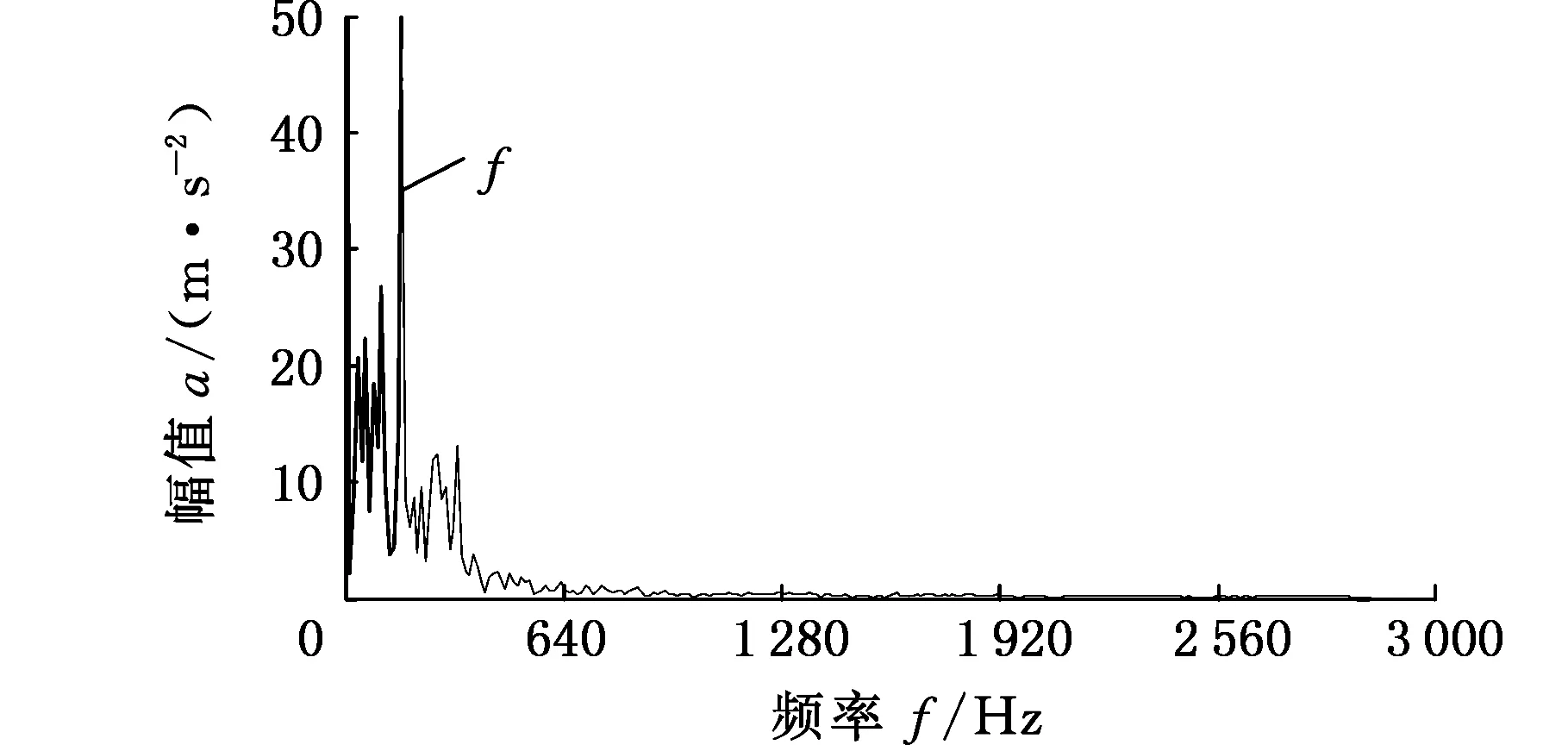
图16 VMD最佳模态函数包络谱(内圈故障)Fig.16 Envelope spectrum of the best mode of VMD (inner ring fault)
同理,利用EMD对滚动轴承故障信号进行处理,得到各模态函数,图17、图18所示分别为经过EMD分解之后得到的各模态函数中的最佳分量及分量的包络谱。
南通一些特定的非物质文化遗产如跳马伕等可以借助于其雄浑的气势、整齐的节奏等表达守土有责、勇敢无畏的意识,而通过演绎钟馗嬉蝠则容易使人在亦庄亦谐的氛围中感受到民间对惩恶扬善、四季平安的期盼。而海安花鼓、十番锣鼓等可让人在享受各种感官盛宴的同时体悟不同文化相互包容借鉴学习的积极意义。
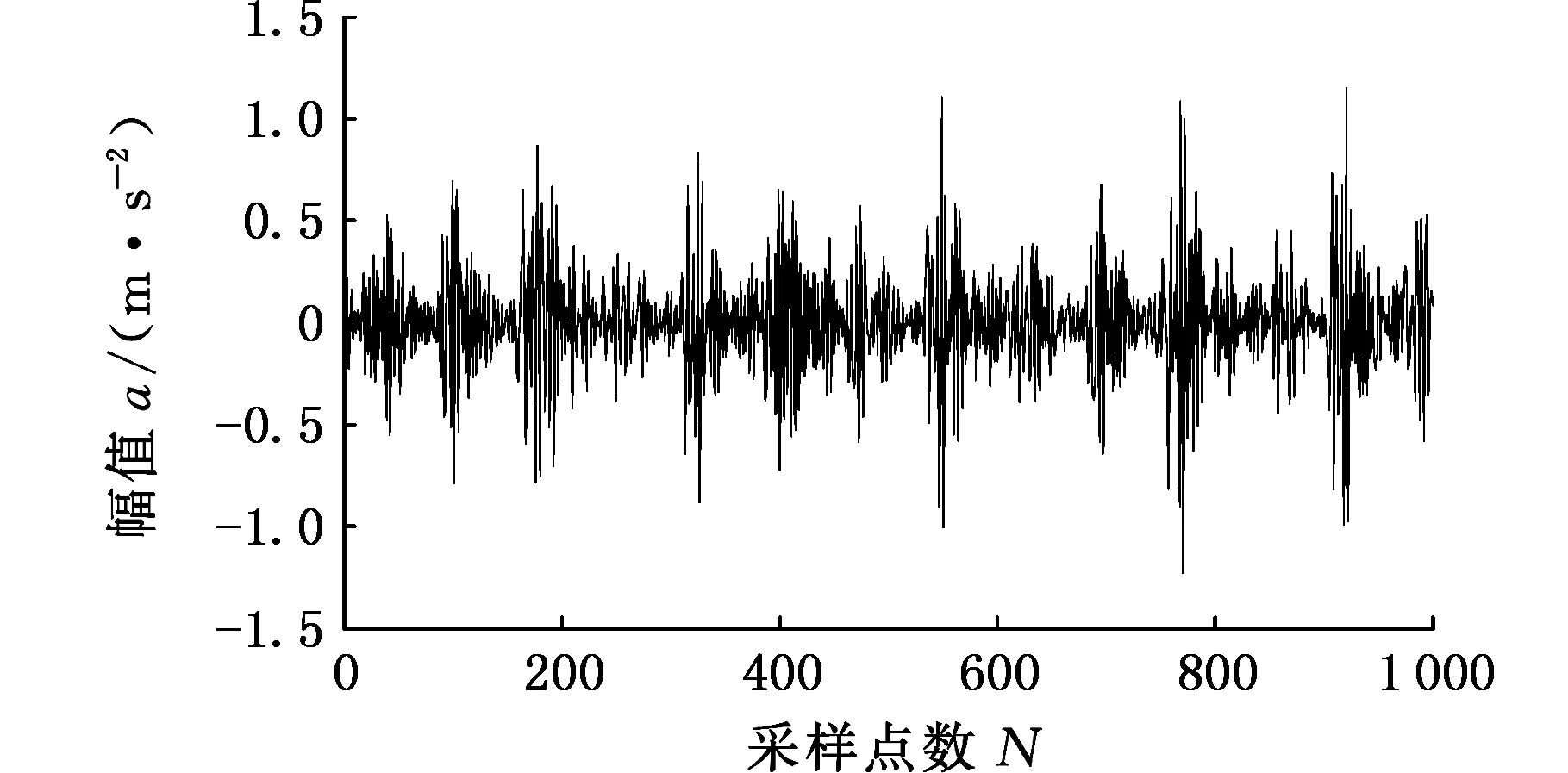
图17 EMD分解得到最佳模态分量(内圈故障)Fig.17 Optimal modal component of EMD (inner ring fault)
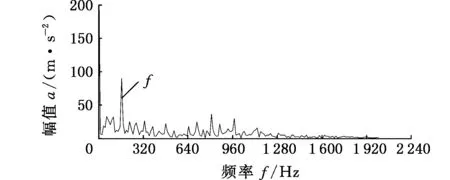
图18 EMD最佳分量包络谱(内圈故障)Fig.18 Envelope spectrum of the best mode of EMD(inner ring fault)
4.3 滚动体故障分析
图19所示为滚动轴承滚动体故障信号的波形图和包络谱图。信号的包络谱的频率处在一个频率带上,很难发现故障信号的特征频率。
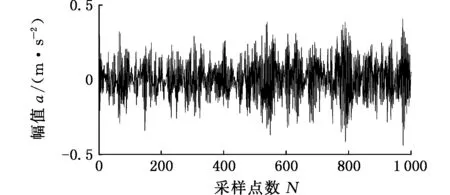
(a)滚动轴承滚动体故障信号波形
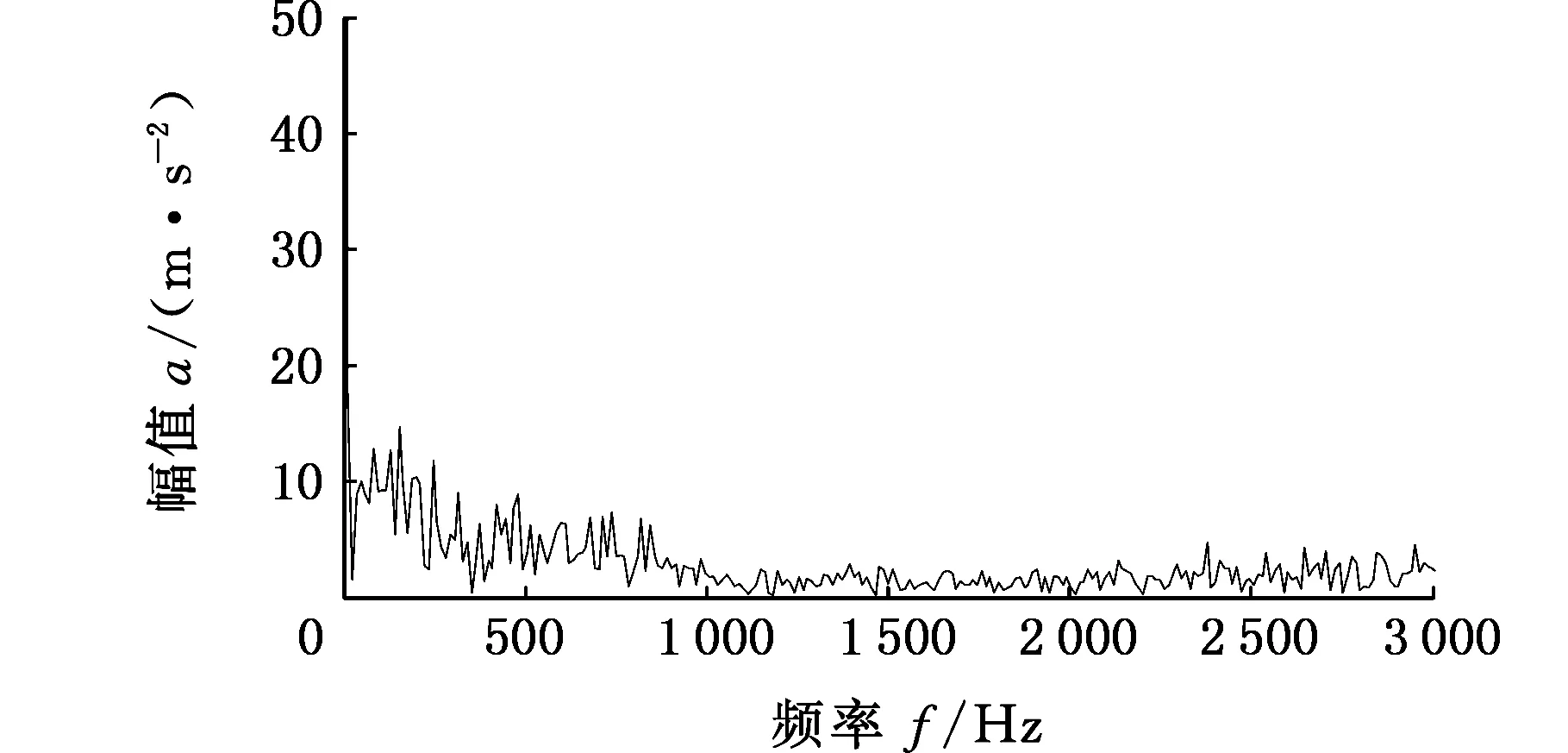
(b)滚动体故障信号包络谱图19 滚动轴承滚动体故障信号波形图及包络谱Fig.19 Waveform diagram and envelope spectrum of fault signal of rolling bearing element
采用蛙跳算法对VMD参数进行优化,得到局部极小熵值的变化曲线,如图20所示,可以看出,群体进化到第4代时得到了局部极小熵值-0.587,对应的最佳组合参数为[6,3 000],以得到优化参数的VMD对外圈故障信号进行处理,得到6个模态函数分量,其中,最佳模态分量的波形图及频谱图见图21,最佳模态分量的包络谱如图22所示。
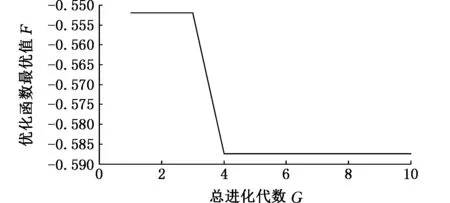
图20 蛙跳算法优化值随进化代数的变化曲线(滚动体故障)Fig.20 The optimized value curve leapfrog algorithmwith the evolution algebra(rolling element fault)
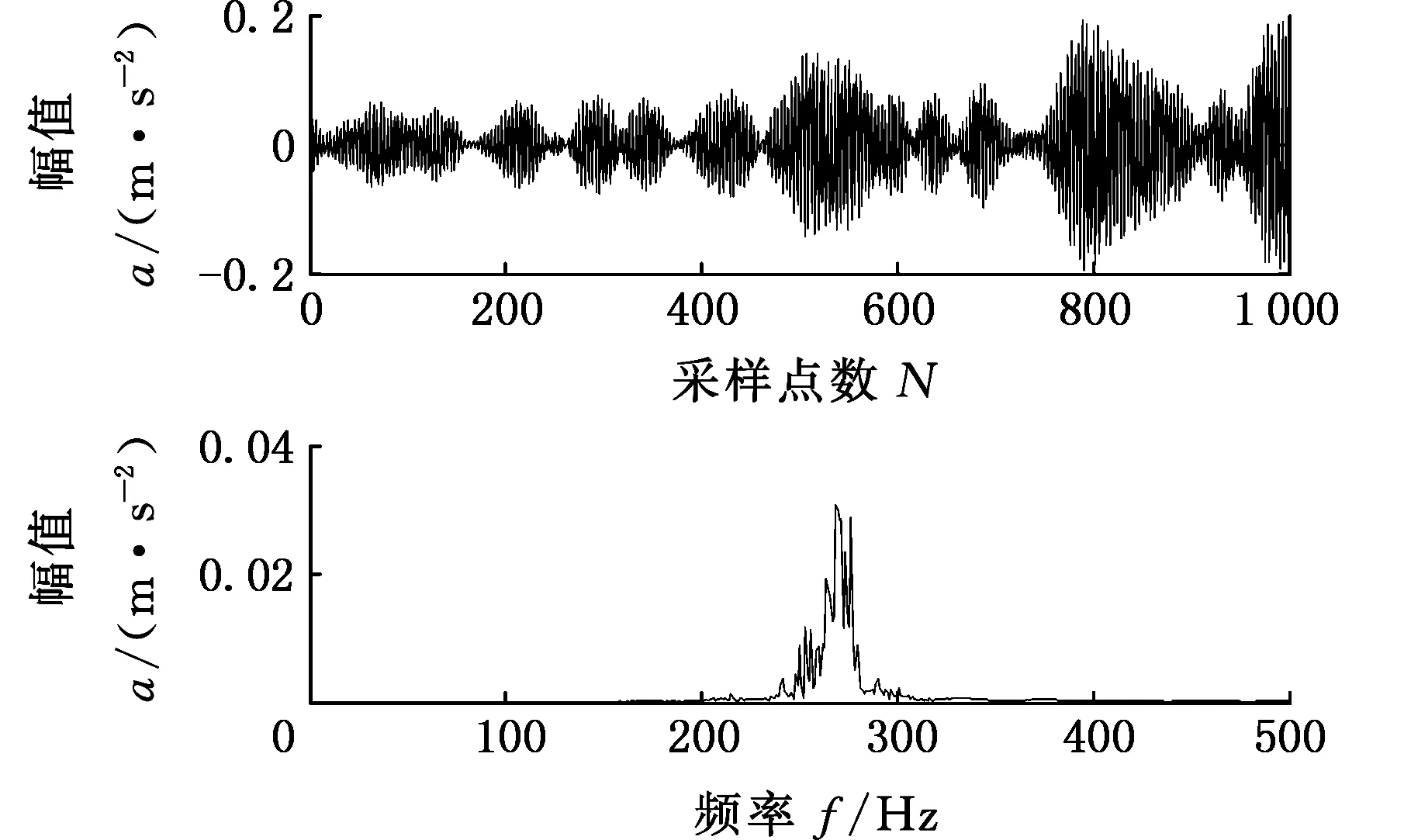
图21 VMD分解得到最佳模态分量Fig.21 Optimal modal component of VMD
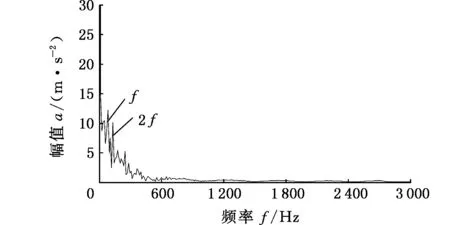
图22 VMD最佳分量包络谱(滚动体故障)Fig.22 Envelope spectrum of the best mode of VMD(rolling element fault)
同理,利用EMD对滚动轴承故障信号进行处理,得到各模态函数,图23、图24所示分别为经过EMD分解之后得到的各模态函数中的最佳分量及分量的包络谱。
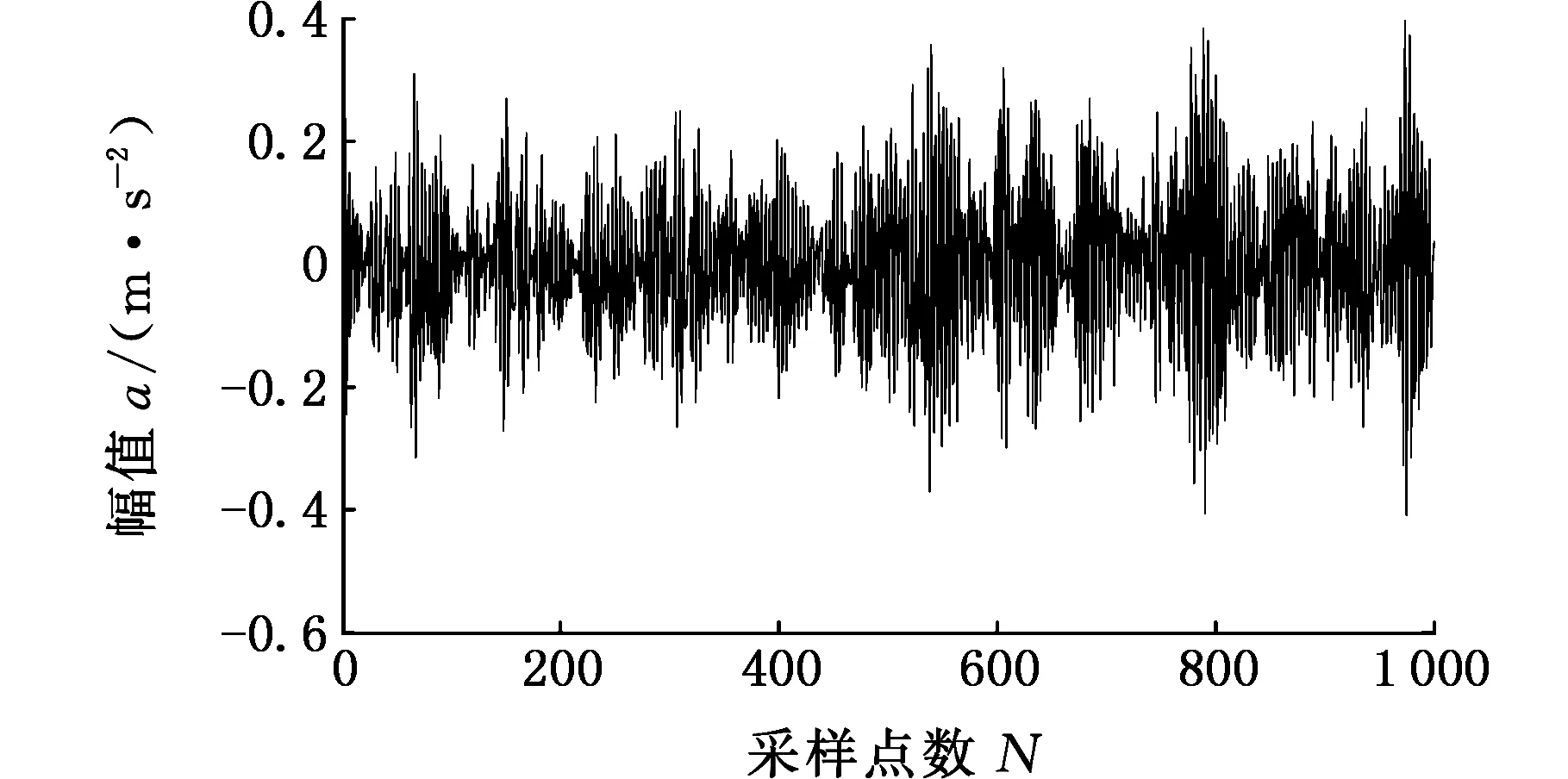
图23 EMD分解得到最佳模态分量(滚动体故障)Fig.23 Optimal modal component of EMD(rolling element fault)
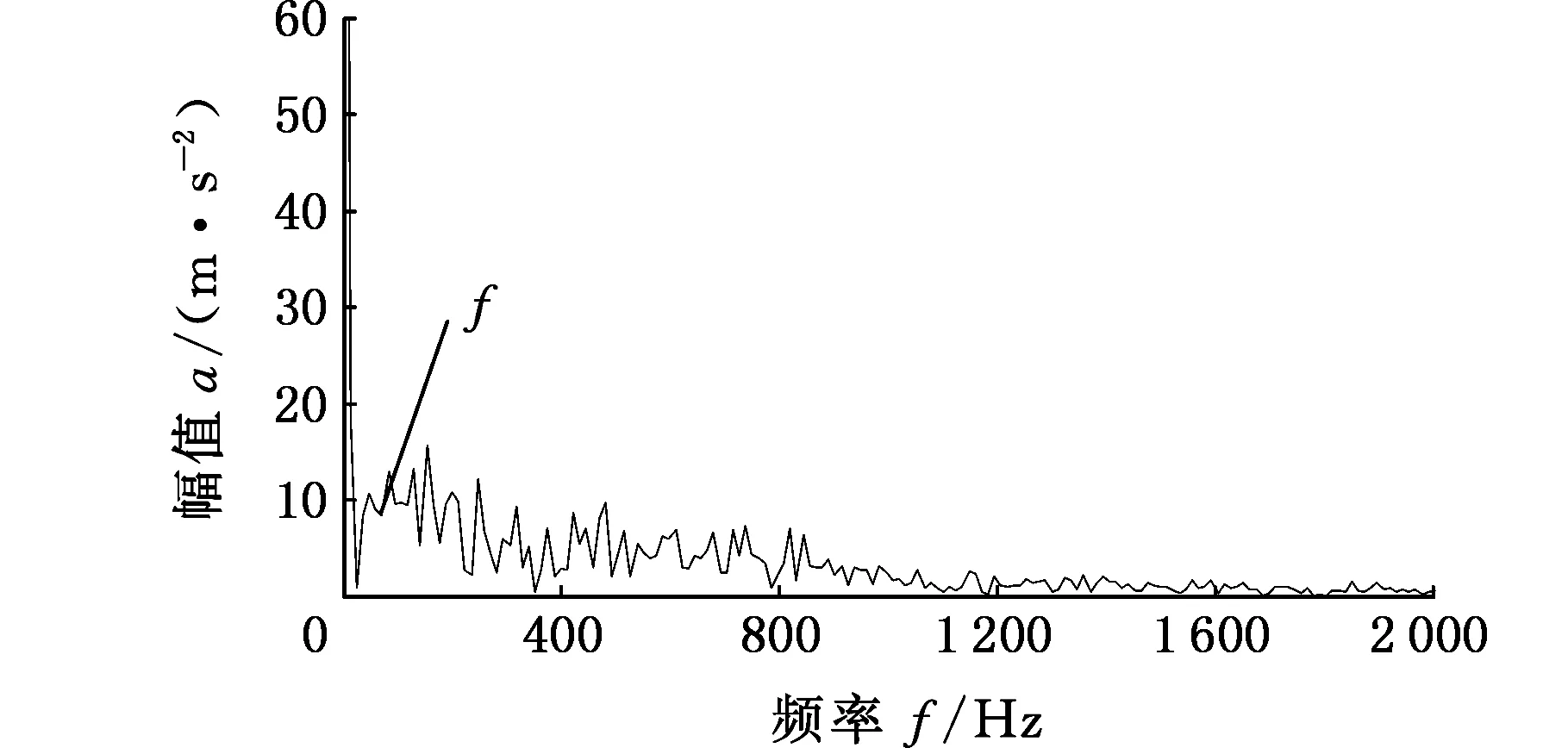
图24 EMD最佳分量包络谱(滚动体故障)Fig.24 Envelope spectrum of the best mode of EMD(rolling element fault)
分别对外圈、内圈、滚动体三种故障进行了VMD分解和EMD分解,得到最佳模态分量,并作包络谱分析。可以看出,外圈故障方面,虽然EMD分解得到的包络谱中也有特征频率,但是还有其他更突出的频率,容易对故障类型误判;内圈故障方面,EMD分解也得到了突出的故障特征频率,但是含有过多的其他频率成分,分解不彻底,存在模态混叠现象;滚动体故障方面,EMD分解没有发现突出的故障特征频率,VMD分解得到了突出的特征频率及其整数倍频率。综上分析可以看出,基于参数优化的VMD分解能够更好地对信号进行完全的分解,对最佳模态函数分量作包络分析能够准确地得到故障特征频率。
5 故障状态识别
对外圈故障、内圈故障和滚动体故障分别采样,各获得50组数据,每组数据包含1 024个采样点。随机抽取各状态中的30组作为训练样本,余下的20组作为测试样本。首先采用优化参数的VMD对各个样本进行分解,得到模态函数,构成矩阵,进行奇异值分解,获得故障信号的特征向量,将得到的特征向量分为训练样本和测试样本。将训练样本作为输入,利用ELM算法进行训练,隐含层节点数L设为30,建立状态识别算法,并利用测试数据进行测试。为了说明ELM故障识别的优势,将同样的训练样本作为BP、SVM、Cg-SVM、PSO-LSSVM的输入,建立识别模型,并用同样的测试样本进行测试。BP隐含层节点个数S设为30;SVM惩罚系数c=1,核宽度系数g=16;Cg-SVM的参数设置如下:惩罚参数C的搜索范围为[0.1,100],高斯核系数σ的搜索范围为[0.1,100];PSO-LSSVM使用粒子群算法对参数寻优,其中,种群规模设为20,最大迭代次数设为200,加速因子C1=1.5,C2=1.7,惩罚参数C的搜索范围为[0.1,100],高斯核系数σ的搜索范围设为[0.01,1 000]。
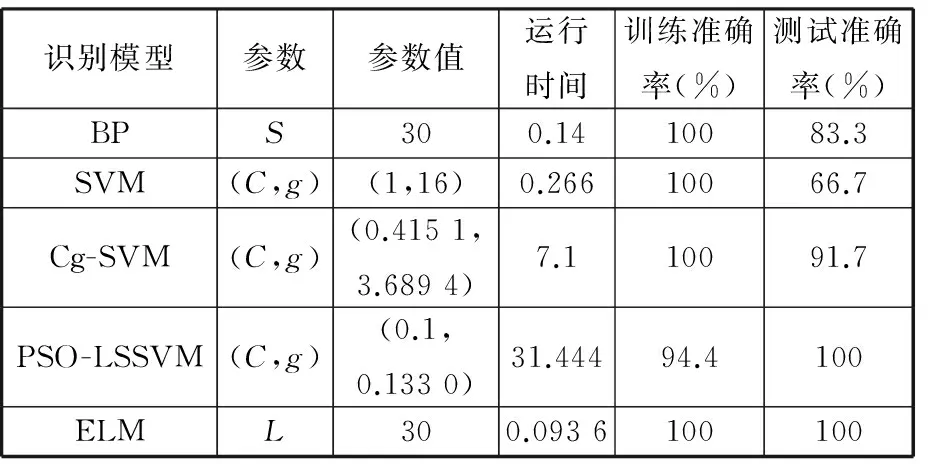
表1 状态识别模型运行的时间与分类的精度
从表1中各组模型识别的结果可以看出,相对于其他4种识别模型,ELM的运行时间较短,且训练和测试的准确率为100%,模式识别效果很好。利用交叉验证和粒子群算法进行参数优化,进而利用SVM或LS-SVM进行模式识别的运行时间较长;Cg-SVM的训练准确率为100%,但是测试准确率低;PSO-LSSVM的测试准确率为100%,但是训练准确率稍低;BP和SVM的测试准确率过低,不能对故障结果进行准确的判断。综上分析,利用ELM对故障模态识别可以大大地提高模式识别的准确率并且缩短运行时间。
6 结论
(1)VMD分解方法可以对信号实现更完整的分解,得到信号从高频到低频段的各模态分量,是一种完全意义上的分解,信号经过VMD分解之后可以更好地获得与故障相关的部分。
(2)VMD在分解中需要确定分解个数和惩罚项系数,这是一组组合参数共同决定分解的效果,利用蛙跳对参数优化,可以避免人为因素的影响,获得最佳的分解效果。
(3)基于蛙跳算法优化的VMD分解结合包络解调分析可以准确、有效地提取出滚动轴承的故障特征信息。
(4)以VMD分解得到的模态函数构成矩阵,进行奇异值分解,将所得到的特征向量作为极限学习机的输入,对故障的类型进行模式识别,并与其他4种模式识别方法做比较,证明了基于极限学习机故障模式识别的的优越性。
[1] 李辉,郑海起,唐立伟.声测法和经验模态分解在轴承故障诊断中的应用[J].中国电机工程学报,2006,26(15):124-128.
LI Hui, ZHENG Haiqi, TANG Liwei. Application of Acoustic Measurement and Empirical Mode Decomposition in Bearing Fault Diagnosis[J]. Proceedings of the Chinese Society of Electrical Engineering, 2006,26 (15): 124-128.
[2] 高强,杜小山,范虹,等.滚动轴承故障的EMD诊断方法研究[J].振动工程学报,2007,20(1):15-18.
GAO Qiang, DU Xiaoshan, FAN Hong, et al. Study on EMD Diagnosis of Rolling Bearing Fault [J]. Journal of Vibration Engineering, 2007, 20 (1): 15-18.
[3] 张俊红, 李林洁, 马文朋, 等. EMD-ICA联合降噪在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2013, 24(11): 1468-1472.
ZHANG Junhong,LI Linjie,MA Wenpeng,et al.Application of EMD-ICA to Fault Diagnosis of Rolling Bearings[J].China Mechanical Engineering, 2013, 24(11): 1468-1472.
[4] 张超,陈建军,郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击,2010,29(10):60-65.
ZHANG Chao, CHEN Jianjun, GUO Xun. A Method of Gear Fault Diagnosis Based on EMD Energy Entropy and Support Vector Machine [J]. Vibration and Shock, 2010,29 (10): 60-65.
[5] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition [J].IEEE Transactions on Signal Processing, 2014, 62(3):531-544.
[6] 陆爽.基于奇异值分解和支持向量机的滚动轴承故障模式识别[J].农业工程学报,2007,23(4):15-20.
LU Shuang. Identification of Rolling Bearing Failure Modes Based on Singular Value Decomposition and Support Vector Machines [J]. Journal of Agricultural Engineering, 2007, 23(4): 15-20.
[7] 苑津莎,张利伟,王瑜,等.基于极限学习机的变压器故障诊断方法研究[J].电测与仪表,2013,50(12):21-26.
YUAN Jinsha, ZHANG Liwei, WANG Yu,et al. Study of Transformer Fault Diagnosis Based on Extreme Learning Machine[J]. Electrical Measurement & Instrumentation, 2013,50 (12): 21-26.
[8] 刘长良,武英杰,甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):3358-3366.
LIU Changliang, WU Yingjie, ZHEN Chenggang. The Variational Modal Decomposition and Fuzzy C Means Clustering [J]. Rolling Bearing Fault Diagnosis Based on China of the CSEE, 2015, 35(13): 3358-3366.
[9] 张鹏军,刘三阳. 求解复杂函数优化问题的混合蛙跳算法[J]. 计算机应用研究, 2009,26(7): 2435-2438.
ZHANG Pengjun, LIU Sanyang. Application of SFLA [J].Computer in Solving Complex Function Optimization Problems, 2009,26(7): 2435-2438.
[10] 薛升翔,贾振红,杨杰,等. 用蛙跳算法优化RBF神经网络参数的研究[J].计算机工程与应用,2011,47(28):59-61.
XUE Shengxiang, JIA Zhenhong, YANG Jie,et al. Using Shuffled Frog Leaping Algorithm to Optimize the Parameters of Radial Basis Function Neural Network[J].Computer Engineering and Application,2011, 47(28): 59-61.
[11] 李辉,郑海起,唐力伟.基于EMD和包络谱分析的轴承故障诊断研究[J].河北工业大学学报,2005,34(1):11-16.
LI Hui, ZHENG Haiqi, TANG Liwei. Study on Fault Diagnosis of Bearing Based on EMD and Envelope Spectrum Analysis [J]. Journal of Hebei University of Technology, 2005,34(1): 11-16.
[12] 唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(5):73-81.
TANG Guiji, WANG Xiaolong. Application of Parametric Optimization Modal Decomposition Method for Early Fault Diagnosis of Rolling Bearing [J]. Journal of Xi’an Jiaotong University, 2015,49 (5): 73-81.
[13] 王卓,田振华,赵丁选. 滚动轴承的振动监测与故障诊断系统[J].机电工程,2001,18(6):52-54.
WANG Zhuo, TIAN Zhenhua, ZHAO Dingxuan. Vibration Monitoring and Fault Diagnosis System for Rolling Bearings[J].Journal of Mechanical & Electrical Engineering, 2001,18(6):52-54.
