基于奇异值分解的ERA改进算法及模态定阶

朱 锐， 杭晓晨， 姜 东,3， 费庆国， 靳文冰

(1.东南大学空天机械动力学研究所 南京，211189) (2.东南大学机械工程学院 南京，210096)(3.南京林业大学机械电子工程学院 南京，210037) (4.国家汽车质量监督检验中心 襄阳，441001)

引 言

结构模态参数识别是动力学的核心内容之一，可以为动响应预示、故障诊断、安全性评估和结构优化设计等提供参考。经过几十年的发展，模态参数识别理论体系已经较为成熟，广泛应用于航空、航天、土木和机械等工程领域。模态参数识别与定阶问题在理论分析和工程应用方面有重要意义。

特征系统实现算法(eigensystem realization algorithm, 简称ERA)是多输入多输出的时域模态参数辨识方法。该方法最初是由Juang等[1]于1984年提出，核心是利用线性系统中Ho-Kalman的最小实现理论来识别系统模态参数。该方法便于确定模态阶次，识别速度较快，同时对具有低频、模态密集特征的结构具有较强的辨识能力。Bazan等[2]研究了特征系统算法中噪声因素对系统极点影响。Zhang等[3]提出了自动特征系统实现算法，并将其应用在朝天门大桥模态试验中。Velazquez等[4]根据线性参数时变技术改进了特性实现算法，将环境振动信号作为算法输入，成功辨识了旋转系统的模态参数。同时，基于奇异值分解[5]的模型定阶方法也是近年来国内外学者关心的问题，一般的定阶方法是从通过奇异值曲线突变特点的角度来考虑。易伟健等[6]提出了残差期望值法和残差期望比法，假设噪声为白噪声，根据白噪声的均值为零的特点确定阶次，但是该方法需多次试算来确定Hankel矩阵维数，计算量较大。周帮友等[7]提出了奇异值插值法，但未深入探讨矩阵维数的确定，同时结果不够直观。赵学智等[8]提出了使用奇异值差分谱的概率来反映信号奇异值曲线的转折点现象。王树青等[9]提出了利用奇异值的相对变换率的概念来确定系统的阶次，该模态定阶方法易受到噪声干扰。

笔者研究基于奇异值分解的改进的特征系统实现算法(improved eigensystem realization algorithm, 简称IERA)，利用结构脉冲响应信号构造初始的Hankel矩阵，根据Cadzow算法[10]重构新的Hankel矩阵。同时针对奇异值归一化指标难以确定模态阶次的现象，采用奇异值百分比(singular value percentage，简称SVP)反映选定阶次增加对系统贡献量，并给出了模态的定价指标(RSVP)。通过仿真算例，研究噪声因素对辨识的模态参数及模态阶次确定的影响，最后将所提方法应用在某三厢车排气系统模态试验中。

1 理论基础

1.1 特性系统实现算法

对于有限、离散时间的线性定常系统,其状态方程可以表示为

其中:x∈Rn，u∈Rm，y∈Rp分别为状态向量、输入向量和输出向量;A，B，C分别为系统的状态矩阵、输入矩阵和输出矩阵。

利用脉冲响应函数构造Hankel矩阵，即

Hrs(k-1)=

(3)

其中:Y(k) ∈RL×P为脉冲响应函数矩阵。

Y(k)=

(4)

其中：hij(k)为k时刻在激励点j和响应点i之间的脉冲响应函数。

由式(1)和(4)可得Y(k)表达式为

Y(k)=CAk-1B

(5)

将式(3)可改写成

Hrs(k)=VrAkWs

(6)

(7)

(8)

其中：Vr∈Rrp×n为可观测矩阵；Ws∈Rn×ms为可控矩阵。

对矩阵Hrs(0)进行奇异值分解

Hrs(0)=PDQT

(9)

其中：P∈Rrp×n；D∈Rn×n；Q∈Rms×n。

由奇异值分解确定的阶次获得系统的最小实现

对矩阵A进行特征值分解，求得特征值矩阵，然后求出特征向量矩阵

Ψ-1AΨ=Z

(12)

其中：Z为特征值矩阵；Ψ为特征向量矩阵

(13)

根据矩阵A的特征值与系统特征值ζr之间的关系确定模态频率ωr和模态阻尼ζr分别为

1.2 改进后算法

传统特征系统实现算法在模态分析过程中，基于奇异值分解后奇异值曲线的突变特点来确定阶次，但是有时候突变并不是很明显，特别在实际工程应用过程中，当噪声污染严重或者模态阶次过高时，大量的噪声模态和计算模态会出现在稳定图[11]上，易出现虚假模态。为剔除原始数据中的噪声[12]，在特征系统实现算法的基础上研究一种根据基于奇异值原理和Cadzow算法改进的特征系统实现算法。Hankel矩阵H由脉冲响应函数构造，包含无噪声的数据信号和噪声信号，用奇异值分解进行去噪。

(17)

(18)

(19)

分析流程如图1所示。通过流程图可以看出，改进后的算法较传统的ERA多进行了一次奇异值分解并进行Hankel矩阵重构。为了保证第1次奇异值分解模态的定阶包含真实的阶次,l1可适当取值稍大同时满足l1≥l2。

图1 改进ERA流程图Fig.1 Flowchart of improved ERA

1.3 模态定阶：奇异值百分比

利用特征系统实现算法进行模态参数识别，需要确定模态阶次[14]。如果选用的阶次低于系统真实的模态阶次，就有可能遗漏真实模态；如果选用的阶次高于系统真实的模态阶次，则识别结果中会呈现较多的虚假模态，对真实模态造成干扰。针对传统奇异值曲线可能出现的突变不明显的特点，以及随着阶次的增加曲线趋向水平渐近线的现象，笔者提出一种奇异值指标——奇异值百分比，能有效地反映所取模态阶次在系统模态参数中的比重，进而有效确定模态的阶次

(20)

从奇异值所占百分比的角度考虑，R为计算矩阵维数，j为选定的阶次，通过百分比反映选定阶次增加对系统贡献量，该指标能有效反应选定阶次在结构中比重。根据奇异值百分比曲线的特点，先确定一个最小预估值，再利用奇异值百分比相邻增量的比值变化的特点作为模态的定阶指标，公式为

(21)

其中:ΔPj+1,j表示为Pj+1-Pj。

因为奇异值百分比反映所选阶次在模态参数中的比重，相邻增量比值会在真实模型阶次附近出现巨大波动。这是因为真实模态以后阶次是噪声成分，其增量在同一量级上，模型的定阶指标(RSVP)将趋于平缓，接近为1，而在真实模态处由于增量的量级不同，会出现一个最小值，在曲线将出现最低处即为模态阶次。其优点是针对受噪声影响奇异值突变不明显、不易确定阶次的现象，通过定义的RSVP，可以有效反应模态阶次值，提高模态的定阶精度。

2 算例研究

仿真模型采用六自由度弹簧-振子系统，验证改进方法在不同噪声工况下的识别能力，同时也验证了在不同噪声工况下采用RSVP指标来确定模态阶次的适用性,并将改进方法应用在某三厢车排气系统模态试验中。

2.1 六自由度弹簧-振子模型

为了验证改进型的算法识别效果的优势及RSVP指标的模态定阶适用性，建立如图2所示的六自由度系统。m1=m6=20 kg,mi=10 kg(i=2,3,4，5)，kj=8×106kN/m,(j=1,2，…，7)。通过模态叠加法确定六阶频率，ci(i=1,2，…，7)的取值使第1阶模态阻尼比为3.00%，其余模态阻尼比为1.00%，如表1所示。

图2 六自由度弹簧-振子系统Fig.2 Six-DOF spring-mass system

表1 系统模态参数Tab.1 System modal parameters

图3 脉冲响应函数Fig.3 Impulse response function

图4 5%白噪声Fig.4 5% white noise simulation

图5 六自由系统稳定图比较Fig.5 Comparison of two stability diagrams of six-DoF system

在质量块m4上施加单位脉冲激励，在mi(i=1,2,…，6)上采集振动位移响应。模型的分析频率f=300 Hz，采样数N=6 000。以m5点输出响应为例，加入5%高斯白噪声后信号曲线与初始曲线不易区分，图3,4为无噪声信号脉冲响应函数(impulse response function，简称IFR)曲线及5%的高斯白噪声曲线。采用传统ERA及改进后算法对含有5%噪声FRF信号进行模态参数识别。图5为两种辨识算法的稳定图。曲线为5%噪声下FRF点表示取不同阶次时识别的频率值，点的颜色反映辨识的阻尼比与理论值的误差。分析可知，改进后算法比传统ERA的稳定图更加简洁，能有效剔除虚假模态，可直观看出改进后算法的辨识阻尼精度更高。

实心点表示归一化奇异值；空心点表示奇异值百分比图6 不同噪声情况下弹簧-振子系统奇异值曲线及百分比Fig.6 Normalized singular values and SVP of spring-mass system under different noise situations

笔者研究5种不同工况下，无噪声以及不同噪声情况下(5%，10%，15%，20%)的模态辨识结果。给出了不同工况下Hankel矩阵奇异值归一化及奇异值百分比，如图6所示。由理论解可知，六自由度系统奇异值定阶指标应为12，在无噪声情况下，奇异值指标在阶次为12发生明显突变，此时奇异值百分比接近为100%，与理论相符。虚线框为突变区域，随着噪声不断增加，突变不断减缓，而百分比不断减低，但在阶次12时，不同工况下百分比仍大于80%。此时，在噪声情况下难以根据奇异值突变的特点确定模态的阶次。给出了模型在4种噪声工况下RSVP值的变换曲线，如图7所示。可以看出，4种不同噪声工况下模态定阶指标(RSVP)都在阶次12后出现最低，故系统的模态阶次为12，与理论值相符，说明在噪声工况下，该定阶方法可以准确地判定系统真实的模态阶次。

表2和表3给出了在4种噪声工况下(工况1,2,3,4分别为5%,10%,15%,20%噪声工况)，传统ERA和改进后算法辨识得到的频率与阻尼比误差值。

由表2可以看出，传统ERA在剔除虚假模态的情况下，ERA与改进后的算法结果的频率误差都较小。表3反映两种算法在不同工况下阻尼比误差。分析可知，高频段的阻尼辨识误差相对较大，阻尼比受噪声的干扰较大。一般表现随着噪声的增加，阻尼辨识误差增大。同时，改进后的算法比传统ERA辨识阻尼比误差较小，识别精度有显著提高。

采用六自由度系统，通过模态叠加法，ci(i=1,2,…，7)的取值使第1阶模态阻尼比为0.30%，其余模态阻尼比均为0.20%。仍以m5点输出响应为例，加入5%噪声信号。采用传统ERA及改进后算法对含有5%噪声FRF信号进行模态参数识别，二种辨识算法的稳定图如图8所示。曲线为5%噪声下FRF通过稳定图结果对比。分析可知，改进后算法比传统ERA的稳定图更简洁，能有效剔除虚假模态。改进后算法的辨识阻尼比与理论值的误差较小，说明阻尼比识别精度更高。

图7 不同噪声情况下模态阶次指标Fig.7 Mode order indicators under different noise situations

表2 模态频率辨识结果误差Tab.2 Error of Identified modal frequencies

表3 模态阻尼比识别误差Tab.3 Error of Identified modal damping ratio

图8 5%噪声下稳定图比较Fig.8 Comparison of two stability diagrams with 5% noise

该工况下Hankel矩阵奇异值归一化及奇异值百分比如图9所示。RSVP值的变换曲线如图10所示。可以看出，该工况下模态定阶指标(RSVP)在阶次12后出现最低，故系统的模态阶次为12，与理论值相符，说明在结构呈小阻尼特性下，该定阶方法仍能准确的判定系统真实的模态阶次。传统ERA已改进后算法辨识结果，如表4所示。分析可知，传统ERA在剔除虚假模态的情况下，针对小阻尼特性结构的情况，ERA与改进后的算法结果的频率误差都较小。同时，改进后的算法比传统ERA辨识阻尼比误差较小，识别精度更高。

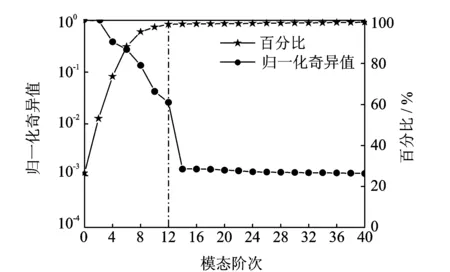
图9 5%噪声下奇异值及百分比Fig.9 Normalized singular values and SVP with 5% noise

图10 5%噪声下模态定阶指标Fig.10 Mode order indicators with 5% noise

2.2 某三厢车排气系统模态试验

研究某三厢车排气系统，主要由前消声器、后消声器两部分组成，如图11所示。将模型用弹性绳悬挂以模拟自由—自由边界条件。模态试验的激励控制、响应测量、数据处理和模态分析，都在LMS Test Lab 11B软件下完成。

图11 某三厢车排气系统传感器分布Fig.11 The sensor placement of a sedan car exhaust system

图12 某三厢车排气系统物理模型Fig.12 Physical model of a sedan car exhaust system

根据文献[15]中的方法和经验选取传感器安装位置，采取单点激励多点测量移动传感器固定锤击点的测量方式，选取了21个测点作为三向传感器的安装位置，以编号20点作为激励点，z方向进行敲击，如图12所示。利用LMS系统测得结构的加速度响应，取14点信号为例，分别给出两种辨识算法的稳定图，如图13所示。

表4 模态参数识别结果Tab.4 Identification results of modal parameters

图13 排气系统稳定图比较Fig.13 Comparison of two stability diagrams of a exhaust system

图14 排气系统奇异值及百分比Fig.14 Normalized singular values and SVP of a exhaust system

分析可知，改进后算法比传统ERA稳定图更加简洁，可以有效剔除虚假模态，便于确定模态阶次；以LMS系统试验值作为参考值，频率点颜色表征识别阻尼比误差的大小。通过对比分析，传统算法识别阻尼比误差整体范围在10%～20%，误差较大，而改进后算法阻尼比误差整体范围在0.0%～6.0%，误差相对较小，故改进后的算法阻尼比误差更小，精度更高。14点处归一化奇异值分百分比曲线如图14所示。根据奇异值百分比大于80%确定一个模态的阶次预设最小值为18。奇异值模态阶次指标如图15所示。在阶次为22时指标将要达到最小值，故系统的模态的阶次22。同时给出了传统ERA与改进后算法辨识结果，表5为表示LMS系统试验测量值与两种算法辨识结果。

图15 排气系统模态阶次指标Fig.15 Mode order indicators of a exhaust system

表5 模态参数辨识结果Tab.5 Identification results of modal parameters

3 结 论

1) 根据奇异值分解原理对特征系统实现算法进行改进，并提出一种判定奇异值阶次的指标——奇异值百分比，根据奇异值百分比曲线的特点，首先确定一个最小预估值，再利用其增量比值变化的特点来确定模态的阶次，在曲线将出现最低处对应着模态真实的阶次。

2) 通过仿真算法辨识验证了改进后ERA的稳定图更加简洁，且阻尼比识别精度更高,研究了噪声因素对辨识参数及模态阶次的影响。结果表明，改进后算法具有更强的抗噪能力，特别是阻尼识别精度更高，同时利用RSVP方法定阶效果更好。

3) 将上述方法应用在某三厢车排气系统模态实验中，识别结果良好，验证了改进ERA和RSVP定阶方法的有效性。

[1] Juang J N, Pappa R S. An eigensystem realization algorithm for modal parameter identification and model reduction[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(5): 620-627.

[2] Bazan F S V. Eigensystem realization algorithm (ERA): reformulation and system pole perturbation analysis[J]. Journal of Sound and Vibration, 2004, 274(1): 433-444.

[3] Zhang Guowen, Ma Jinghua, Chen Zhuo, et al. Automated eigensystem realization algorithm for operational modal analysis[J]. Journal of Sound and Vibration, 2014, 333(15): 3550-3563.

[4] Velazquez A, Swartz R A. Output-only cyclo-stationary linear-parameter time-varying stochastic subspace identification method for rotating machinery and spinning structures[J]. Journal of Sound and Vibration, 2015, 337: 45-70.

[5] Jiang Huiming, Chen Jin, Dong Guangming, et al. Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015, 52: 338-359.

[6] 易伟建, 刘翔. 动力系统模型阶次的确定[J]. 振动与冲击, 2008, 27(11): 12-16.

Yi Weijian, Liu Xiang. Order identification of dynamic system model[J]. Journal of Vibration and Shock, 2008, 27(11): 12-16. (in Chinese)

[7] 周帮友, 胡绍全, 杜强. 特征系统实现算法中的模型定阶方法研究[J]. 科学技术与工程, 2009 (10): 2715-2716.

Zhou Bangyou, Hu Shaoquan, Du qiang. Study about calculation the order of model in eigensystem realization algorithm[J]. Science Technology and Engineering, 2009 (10): 2715-2716. ( in Chinese)

[8] 赵学智, 叶邦彦, 陈统坚. 基于奇异值曲率谱的有效奇异值选择术[J]. 华南理工大学学报:自然科学版, 2010, 38(6):11-18.

Zhao Xuezhi, Ye Bangyan, Chen Tongjian. Selection of effective singular values based on curvature spectrum of singular values[J]. Journal of South China University of Technology: Natural Science Edition, 2010, 38(6):11-18. (in Chinese)

[9] 王树青, 林裕裕, 孟元栋, 等. 一种基于奇异值分解技术的模型定阶方法[J]. 振动与冲击, 2012, 31(15): 87-91.

Wang Shuqing, Lin Yuyu, Meng Yuandong, et al. Model order determination based on singular value decomposition[J]. Journal of Vibration and Shock, 2012, 31(15): 87-91. (in Chinese)

[10] Cadzow J A. Signal enhancement-a composite property mapping algorithm[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(1): 49-62.

[11] Mohanty P, Rixen D J. Modified ERA method for operational modal analysis in the presence of harmonic excitations[J]. Mechanical Systems and Signal Processing, 2006, 20(1): 114-130.

[12] Sanliturk K Y, Cakar O. Noise elimination from measured frequency response functions[J]. Mechanical Systems and Signal Processing, 2005, 19(3): 615-631.

[13] Golafshan R, Sanliturk K Y. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J]. Mechanical Systems and Signal Processing, 2016, 70: 36-50.

[14] Sau-Lon James Hu, Bao Xingxian, Li Huajun. Model order determination and noise removal for modal parameter estimation[J]. Mechanical Systems and Signal Processing, 2010, 24(6): 1605-1620.

[15] 费庆国, 李爱群, 缪长青, 等. 基于主列筛选的动态测试传感器配置方法研究[J]. 力学学报, 2008, 40(4): 543-549.

Fei Qingguo, Li Aiqun, Miao Changqing, et al. Vibration sensor placement method based on principal subset selection[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(4): 543-549. (in Chinese)