电磁滑环式在线动平衡系统特性分析与实验

张 珂， 张驰宇， 张丽秀， 吴玉厚

(沈阳建筑大学机械工程学院 沈阳，110168)

1 问题的引出

数控机床是先进制造的基础装备，主轴是机床的关键部件，对加工质量有直接影响。高速主轴系统是精密部件，过大的不平衡振动可能引起系统的损伤。在线动平衡可以实现高速主轴在运转状态下达到要求的平衡状态，并可以根据机床工作条件的变化进行实时调整。在线动平衡装置的优劣程度决定着高速主轴的工作性能和使用寿命，对产品的质量和生产效率有巨大影响。

目前，机床主轴在线动平衡装置共分3类，即直接式、间接式和混合式，如表1所示。

表1 机床主轴在线动平衡装置分类Tab.1 Classification of spindle balancer during operation

直接式动平衡的基本原理是通过比较直接的方法改变转子的重心位置，主要包括激光去重式[1]、喷涂式[2]和液体式[3-4]。直接式装置平衡能力有限，且不适合高速。间接式动平衡装置的基本原理是依靠电磁力给转子系统长期提供一个和不平衡力大小相等、方向相反的力。按照施力方式的不同，主要分为两种形式:电磁轴承型[5]和电磁圆盘型[6]。由于系统一直受到电磁力的作用，不必要的能耗很大。此外，这类平衡装置结构复杂，几何尺寸大。混合式动平衡装置的基本原理是改变平衡装置内部的质量分布，从而实现动平衡。根据配重的驱动方式不同，主要分为被动式[7]、机械式[8]和电磁式[9]。被动式装置中，带黏性阻尼的质点在转子槽中做自由运动，旋转中自适应地降低不平衡，装置结构简单，可实时调整，但在主临界转速附近会出现周期性的大幅振动。机械式装置的基本原理是采用电机移动配重，装置结构复杂，不适用于高速旋转的大型主轴系统。

图1(a)为电磁滑环式平衡头结构示意图，配重盘(动环)由轴承支承随转子旋转，配重盘上有极性相间的永磁体，工作时由相对固定的磁性板(静环)提供电磁力驱动配重盘旋转，从而改变转子的质量分布。图1(b)为磁性板结构，有交错的凸台和凹槽。

目前，国内学者研究的平衡头主要集中在混合式，但主轴工作转速一般在5kr/min以下，且处于实验室阶段。国外的主轴在线动平衡研究已有各种应用产品，其中电机驱动式、电磁驱动式平衡头有广泛应用。美国SCHMITT公司的SBS内置平衡头[10]用在磨削主轴内，平衡能力为100～7 000 g·cm，适合转速为300～13 000 r/min。美国Kennametal公司推出的整体自动平衡系统 (total automatic balancing system，简称TABS)[11]将两个平衡环设置在刀柄上，通过电磁力调节平衡环的相对位置，2s内即可使主轴回转精度达到50 nm以下。意大利MARPOSS公司推出的主轴型(ST)平衡头[12]安装在磨床主轴内，适合转速为1 100～6 500 r/min，平衡能力为400～13 000 g·cm。德国Hofmann公司推出的电磁滑环式平衡头AB 9000[13]，适合转速为200～120 000 r/min，平衡能力为100 g·mm～3.2 kg·m。文献[14]发表了关于电磁平衡环的研究文章。文献[15]也开始了该类装置的研究,使振动峰值降低约80%。文献[16]进行了电磁滑环式平衡头的结构设计并进行了后续研究。文献[17]开发出一套基于LabVIEW的算法，能测出动不平衡力大小、位置和方向。

图1 电磁滑环式平衡头结构Fig.1 Structure diagram of electromagnetic ring balancer

高速数控机床主轴自身产生的振动主要有3个方面：共振、不平衡引起的振动以及电主轴的电磁振动。当主轴的工作转速与自身固有频率重合时，将产生共振。主轴高速运行时，任何微小的不平衡质量都将引起主轴不同程度的机械振动。机械主轴使用带传动，因此电磁振动不予考虑，但与主轴密切相关的电机和皮带的振动却不容忽视。

高速主轴因自身固有的特性及工作参数，导致其动平衡装置需满足特殊要求。高速主轴转速高，不平衡引起的振动比较明显，在转速超过一阶临界转速后，轴系将从刚性进入柔性状态，这时不能只采用对待刚性转子的平衡方法[18]。机床工况复杂，平衡装置需要适应不同工作条件。平衡装置的尺寸应尽量小，对主轴产生的不良影响也要尽量小。装置应平衡快、冲击小、效果稳定，尽量采用动开式，可以更加稳定、节能并减少干扰。

笔者研究的电磁滑环式在线动平衡装置与其他动平衡装置相比，具有以下优点：a.结构简单、尺寸小、质量轻；b.用电磁力驱动，动作时间短、无摩擦磨损；c.利用磁力形成无接触自锁，机械零件大大减少，适用转速高。但是，电磁滑环式平衡装置的造价比其他平衡装置高，且市场上的成熟产品被外国公司垄断。

2 电磁滑环式在线动平衡装置

文献[9]对于电磁滑环式在线动平衡装置的原理进行了清楚阐述。平衡装置主要由静环和动环两部分组成。图2为实验室采购的平衡头的照片。静环主要由线圈和齿形铁磁环组成；动环主要由轴承支承的配重盘组成，是形成动平衡补偿矢量的元件。装置内两个配重盘相对转动，合成一个矢量，即为校正质量。

图2 电磁滑环式平衡头照片Fig.2 Electromagnetic ring balancer

图3为电磁滑环的动作原理。静环由高磁导率的材料制成，有凸台与凹槽相间的结构，凸台与凹槽的长度等于动环上永磁铁的间距，其作用是稳定平衡位置并传递线圈产生的电磁场。当线圈激励时，铁齿与配重盘上的永磁体相互作用，实现步进，当线圈激励结束后，配重盘稳定在下一个位置不动。

图3 电磁滑环的动作原理Fig.3 Action principle of electromagnetic ring

3 在线动平衡系统特性分析与实验

3.1 影响系数法

传统的现场动平衡技术主要有试重周移法、三点法和二点法等。这些方法存在启动次数多、精度差和对机器损伤大等弊端。影响系数法可以比较精确地求出应加重量的大小和方向，起动次数少。

首先，主轴不加试重，起动至待平衡转速，测量原始振动位移的幅值和相位A0，然后停机加试重P至转子上，P为试重质量与半径的乘积，即

P=mr

(1)

其中：m为试重的质量(g)；r为试重位置的半径(mm)。

然后，重新起动至相同的转速，测量加试重后振动位移的幅值和相位A1，计算影响系数

(2)

其中：K为影响系数(μm/(g·mm))；A0为原始振动量 (μm)；A1为加试重后的振动量(μm)。

进而得到补偿质量为

(3)

其中：Q为补偿质量，其大小为补偿质量与半径的乘积(g·mm)。

3.2 实验平台设计

图4为实验平台的组成，主要包括平衡头、主轴、电机、传感器、底座、控制器、数采器和上位机。主轴为SYL04H-1型机械主轴，空心结构。平衡头安装在主轴内孔中，内部采用若干霍尔传感器用于测量相位和转速。振动的测量采用电涡流位移传感器。主轴与电机之间为带传动，传动比为1∶1。主轴采用柔性支承以减少支承的刚度，使主轴的振动更加明显易测并减少外界干扰。控制器和数采器的软、硬件均采用美国NI公司的LabVIEW系列。

图4 实验平台的组成Fig.4 Composition of experiment platform

3.3 实验与结果分析

3.3.1 转速对实验平台振动的影响

首先考察实验平台的振动特性，测量不同转速下实验平台各处的振动情况。实验从300 r/min连续升至4 200r/min，每次提高300r/min，测试了主轴前端、主轴后端、平台底座和电机外壳的振动。图5为实验平台各处振动幅值对比。可以看出，在1 800 r/min附近，振动幅值剧烈增大，现场可观察到位移探头产生了肉眼可见的振动，整个测试平台产生了共振，不能准确测量主轴的振动，应当避免这些转速。此外，平台振动的幅度与平台的位置是有关系的。测量主轴前端时，传感器安置在底座靠中部位置，振动幅度小。测量电机和主轴后端时，传感器安置在底座边缘，振动幅度大。在其他速度时，底座和电机振动很小，但超过3 600r/min以后，主轴后端的振动增大。结合文献[19]，可能是带传动对主轴的振动产生了影响，需要进一步的分析和实验。

图5 实验平台各处振动幅值对比Fig.5 Comparison of vibration throughout the platform

3.3.2 转速对在线动平衡系统动平衡效果的影响

机床主轴在低速运转时，主轴可以看成是刚性系统，进行动平衡后，其效果比较稳定。在高速下，主轴系统可能会进入柔性状态，这时按照刚性轴的动平衡方法进行动平衡，其效果在其他转速不一定好。此时系统已经越过一阶临界转速，进入柔性状态，动平衡的效果可能会受到转速改变的影响。

实验中首先测量主轴在3 300，3 600，3 900和4 200 r/min下未进行动平衡的振动量；然后在3 600 r/min下对主轴进行动平衡并测量其振动量，再改变转速分别在3 300，3 900和4 200r/min下测量；之后类似地依次在3 900和4 200r/min进行动平衡，然后改变转速测量。图6为主轴在不同转速下动平衡后的效果对比。可以看出：在3 600 r/min动平衡后，降速至3 300 r/min，振动幅值基本不变，升速到3 900和4 200 r/min，振幅提高；在3 900 r/min动平衡后，降速或升速，振幅都有不同程度的提高；在4 200 r/min动平衡后，降速或升速，振幅也有不同程度的提高。

可见，改变转速对动平衡效果有影响，因为主轴已经越过临界转速，工作在柔性状态，这时不能单纯按照刚性轴的动平衡方法，应当采用柔性轴的动平衡方法对主轴进行模态分析和多面平衡。此外，系统在3 300和3 600 r/min、在3 900和4 200 r/min的变化规律相似。

图6 主轴在不同转速下动平衡的效果对比Fig.6 Comparison of the balancing results at different speeds

3.3.3 试重角度对影响系数及动平衡效果的影响

在平衡过程中，试重的试加位置和大小对动平衡起着重要的影响。若试重过小，对振动情况没有明显影响；若试重过大，可能会极大地增加振动，造成设备的损坏，试加位置的选择也具有同样的道理。目前，对于加试重没有精确的计算值，只有一些经验公式，本系统拟用振动幅值和相位变化较大时的影响系数。

实验在主轴端面不同角度试加相同质量(8.1g)的配重，测量试重前后的振动情况，得到对应于实验角度的若干组幅值差值和相位差值。根据式(2)得到在不同角度试重的影响系数。图7为试重前后，振动的幅值差值和相位差值，与试重角度以及计算得到的影响系数幅值之间的关系。其中，幅值差值与相位差值一一对应，影响系数的大小由图中符号的大小体现，并标明数值(单位为10-3μm/(g·mm))。可以看出，幅值和相位变化越大，影响系数越大，而在15°处，相位差值接近零，影响系数最大。

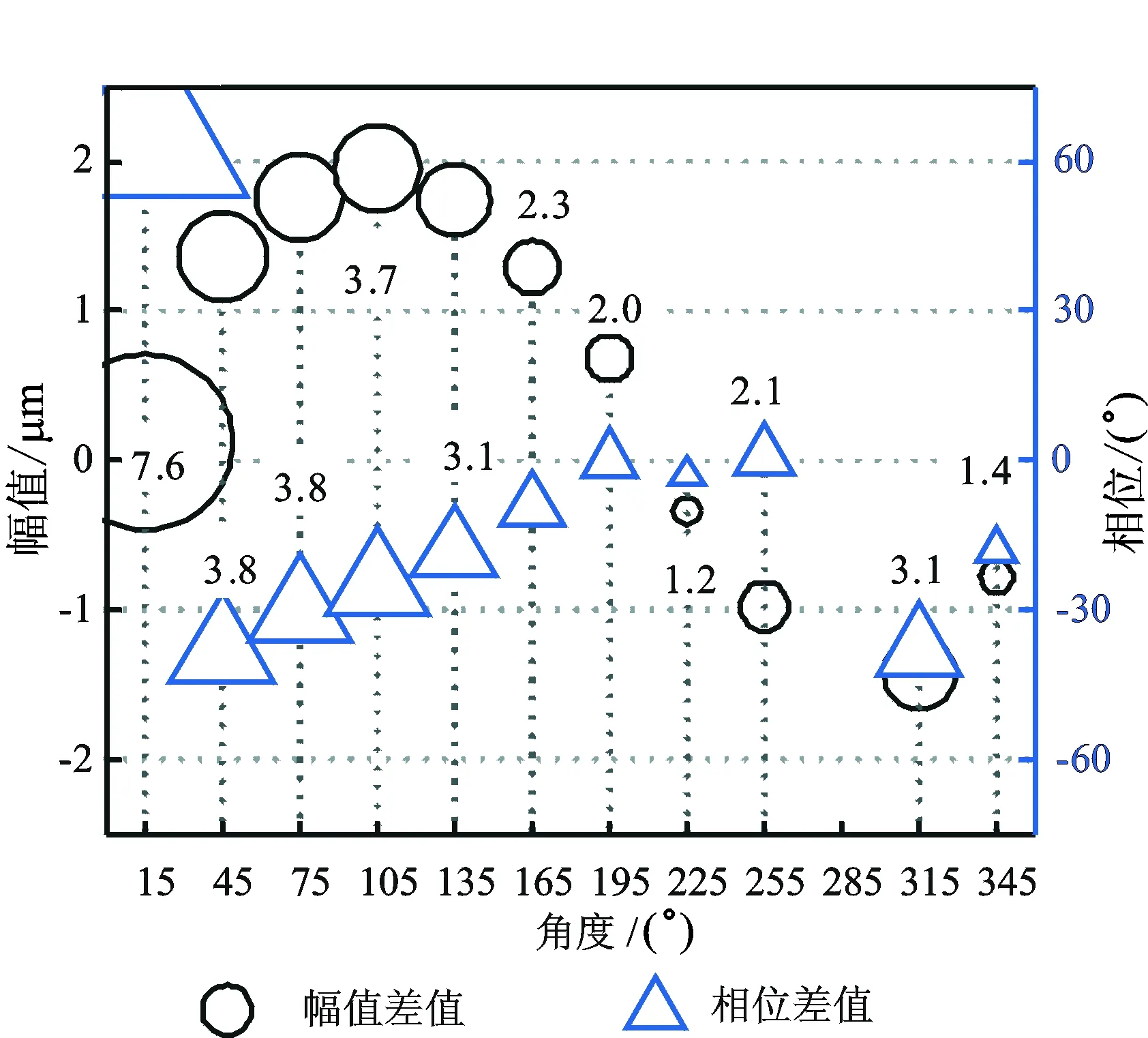
图7 幅值差值和相位差值与试重角度及影响系数幅值的关系Fig.7 Relationship among the difference value of vibration amplitude and phase, the angle of test weight and the impact amplitude coefficient

根据图7选取了两个幅值和相位变化都比较大的点(75°和315°)，以及两个幅值或相位变化较小的点(15°和195°)进行加试重动平衡实验，比较动平衡前后的振动情况。图8为在不同角度加试重后的动平衡效果对比。实验结果表明：将试重加在15°，75°和195°时，动平衡效果不好；在315°时，动平衡效果较好；在75°时，因为振动量过大，超出了设备的平衡能力，所以无法将振动降到理想程度，但幅值下降的程度仍然好于15°和195°。可见，实验结果符合预期，即振动幅值和相位变化都比较大时，影响系数较可靠且幅值较大。

图8 在不同角度加试重后的动平衡效果对比Fig.8 Comparison of balancing effect in different angles of test weight

4 结 论

1) 实验研究了电磁滑环式在线动平衡系统的特性，结果表明该系统可以用于高速主轴动平衡，其结构简单、性能可靠。使用该装置对实验主轴进行动平衡，在获得可靠的影响系数的条件下，最高可以将振幅降低91%。

2) 转速对于在线动平衡系统有很大影响，主要体现在：a.在临界转速附近实验平台本身会产生共振，振动程度几倍于其他转速，会严重影响动平衡的效果；b.主轴越过临界转速后，工作在柔性状态，动平衡的效果只能在一定转速范围内保持，这时不能单纯按照刚性轴的动平衡方法，应当采用柔性轴的动平衡方法对主轴进行模态分析或双面动平衡。

3) 使用影响系数法进行动平衡时，获得可靠的影响系数非常重要，实验针对试重角度进行了研究。结果表明，在试加配重后，振动的幅值和相位改变都比较大的情况下，可获得比较可靠的影响系数。

[1] 周继明, 欧阳光耀. 动不平衡质量不停机自动切除初探[J]. 传感器技术, 1998,17 (4): 13-16.

Zhou Jiming, Ouyang Guangyao. Preliminary exploration on cutting off dynamic unequilibrium mass automatically with non stop machines[J]. Journal of Transducer Technolog, 1998,17 (4): 13-16. (in Chinese)

[2] Gusarov A A, Ssccol C, Shatalov L N. Automatic balancing of rotor [C]∥2nd International Conference on Vibration in Rotating Machinory. London: Institution of Mechanical Engineers, 1980: 457-461.

[3] Birkenstack D, Jager O. Multi-chambered fluid balancing apparatus： US,3950897A[P]. 1976-04-20.

[4] 白彩波. 高速主轴在线动平衡头的研制[D]. 北京：中国计量学院,2012.

[5] 李红伟, 徐旸, 谷会东, 等. 电磁轴承-挠性转子系统的本机动平衡方法[J]. 中国机械工程, 2008, 19(12): 1419-1422.

Li Hongwei, Xu Yang, Gu Huidong, et al. Field dynamic balancing method in AMB-flexible rotor system[J]. China Mechanical Engineering, 2008, 19(12): 1419-1422. (in Chinese)

[6] 黄立权, 王维民, 苏奕儒, 等. 基于电磁自愈力的转子自动平衡方法与实验研究[J]. 振动与冲击, 2011, 30(1): 208-212.

Huang Liquan, Wang Weimin, Su Yiru, et al. Rotor automatical balancing method and test based on electromagnetic self-recovery force[J]. Journal of Vibration and Shock, 2011, 30(1): 208-212. (in Chinese)

[7] Thearle E L. Automatic dynamic balancers (pant 1 leblanc balancer) [J]. Machine Design, 1950, 22(9): 119-124.

[8] Vegte J V. Continuous automatic balancing of rotating systems[J]. Journal of Mechanical Engineering Science, 1964, 6: 264-269.

[9] Hildebrand S, Miller L. Rotating machine active balancer and method of dynamically balancing a rotating machine shaft with torsional vibrations: US, 20060005623A1[P]. 2006-06-12.

[10] Schmitt Industries Inc. SBS balancers [EB /OL]. (2016-04-25). http:∥www.grindingcontrol.com/products/

[11] 周大帅, 伍良生. 机床主轴在线动平衡技术综述[J]. 现代制造工程, 2008(7): 121-124.

Zhou Dashuai, Wu Liangsheng. The summarize of online balancing machine tool spindle[J]. Modern Manufacturing Engineering, 2008(7): 121-124.(in Chinese)

[12] The Companies of Marposs Group. Balancing heads [EB/OL]. (2016-04-25).http:∥www.marposs.com/product.php/eng/grinding_wheel_balancer

[13] Hofmann. Ring balancer AB 9000[EB /OL]. (2016-04-25).http:∥www.hofmann-balancing.co.uk/products/active-balancing-systems/ring-balancer-ab-9000.html

[14] Moon J K, Kim B S, Lee S H. Development of the active balancing device for high-speedspindle system using influence coefficients[J]. International Journal of Machine Tools & Manufacture, 2006, 46: 978-987.

[15] 沈伟. 旋转机械主动平衡技术及工程应用研究[D]. 北京: 北京化工大学, 2006: 12-60.

[16] 樊红卫, 景敏卿, 刘恒, 等. 电磁环形自动平衡装置的结构设计与计算[J]. 机床与液压, 2012, 13: 1-4.

Fan Hongwei, Jing Minqing, Liu Heng,et al. Structural design and calculation of electromagnetic ring automatic balancer[J]. Machine Tool & Hydraulics, 2012,13:1-4.(in Chinese)

[17] 张珂, 李桐, 邓华波, 等. 一种电主轴在线动平衡测试算法[J]. 沈阳建筑大学学报:自然科学版, 2016, 32(1): 148-155.

Zhang Ke, Li Tong, Deng Huabo, et al. A motorized spindle online dynamic balance testing algorithm[J]. Journal of Shenyang Jianzhu University: Natural Science, 2016, 32(1): 148-155.(in Chinese)

[18] 王正浩, 孙成岩, 刘大任, 等. 基础柔性的转子系统振动模态分析[J]. 沈阳建筑大学学报: 自然科学版, 2013, 2: 367-371.

Wang Zhenghao, Sun Chengyan, Liu Daren, et al. Vibration modal analysis of rotor system based on flexible foundation[J]. Journal of Shenyang Jianzhu University: Natural Science, 2013, 2: 367-371. (in Chinese)

[19] 李滨城, Hirsch A. 带传动的横向振动对机床主轴偏移的影响[J]. 现代机械, 2005, 6: 16-17.

Li Bincheng, Hirsch A. The influence of transverse vibration in belt drives on displacement in the end of spindle[J]. Modern Machinery, 2005, 6: 16-17.(in Chinese)