线性时变时滞连续-离散描述系统鲁棒故障诊断滤波器设计

梁天添，王 茂

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

对于实际系统而言，执行器或传感器发生故障可能导致系统非正常工作。例如，在卫星交会对接的操作中，对卫星姿态跟踪控制的研究是非常必要的[1]，而执行器或传感器失效将造成卫星姿态控制系统的非正常工作从而导致对接失败。因此，系统的故障诊断问题具有现实意义。对于一些实际系统[2-4]，描述系统（又称广义系统或奇异系统）因具有比状态空间方法更好的表征特性，得到了越来越多的重视。本文正是基于该背景对描述系统的故障诊断问题进行研究。

对于描述系统故障诊断问题，故障诊断观测器/滤波器的设计是一种行之有效的方法。文献[5]针对基于描述系统模型的离散时间系统，设计了残差容许且符合H∞性能指标的故障检测滤波器。文献[6]针对具有不确定性的描述系统，设计了增广比例微分（PD）观测器，其增广残差对于传感器噪声、未知扰动及不确定性具有鲁棒性。文献[7]针对具有执行器/传感器扰动和未知结构非变参数不确定性的非线性描述系统设计了鲁棒H∞自适应故障估计观测器，该观测器同样适用于正常非线性系统的故障估计。对于线性变参数（LPV）描述系统，文献[8-10]研究了其故障诊断/检测观测器的设计问题。

大多数实际系统中存在状态时滞现象，因此研究时滞描述系统的故障诊断问题具有尤为重要的意义。文献[11-12]分别针对具有不确定性的线性连续时间常数时滞和时变时滞描述系统设计了故障诊断滤波器，其核心是将滤波器视为残差生成器，并将滤波器设计问题转化H∞为滤波问题。文献[13]针对基于描述系统的时变时滞马尔科夫跳变系统，设计了马尔科夫自适应（Markovian Adaptive）观测器。文献[14]针对具有非线性扰动及时变网络交换时滞的非线性跳变描述系统提出了一种新的时滞依赖观测器。

在上述有关时滞连续-离散描述系统故障诊断研究方法中，故障诊断观测器/滤波器均基于奇异结构，实现非常困难。为更精确估计描述系统的故障，急需一种新形式的故障诊断滤波器。在文献[15-17]中，作者提出一系列非奇异结构的故障诊断观测器/滤波器，以实现描述系统的故障诊断，这给本文带来了启示。本文针对一类具有惯性传感器元件的时变时滞连续-离散描述系统，提出了一种新的非奇异结构的基于观测器的故障诊断滤波器。该滤波器基于增广量测残差实现，且增广量测残差满足鲁棒H∞性能指标，即增广量测残差对于故障及增广扰动具有鲁棒性。对于时变时滞描述系统，其滤波器参数矩阵不是标准的LMI。为此，引入CCL算法以解决该问题。为尽早检测出故障，引入残差评价函数及阈值以判断故障是否发生。

本文安排如下：第2节引入参数并使用Euler离散化方法，将时变时滞连续-离散描述系统转化为一般系统。第3节提出非奇异结构的基于观测器的故障诊断滤波器，引入 Lyapunov-Kravoskii方程以证明符合鲁棒H∞性能指标的滤波器参数矩阵的存在条件，引入锥补线性化（CCL）算法对符合线性矩阵不等式（LMI）的参数矩阵不等式进行辅助运算，引入残差评价函数及阈值以判断故障是否发生。第4节提出仿真算例以验证设计方案有效性。第5节得出结论。

1 问题描述

首先考虑如下连续-离散时滞描述系统模型：

其中，x∈Rn为系统状态向量，u∈Rp为系统输入，y∈Rm是系统输出，w∈Rd为系统扰动，f∈Rq为传感器故障，E∈ Rn×n可能为奇异矩阵，即rank(E)=r≤n，d1(t)为时变时滞，且满足 0≤τm≤d1(t)≤τM，τm、τM为已知常数，φ()为[-τM,0]上的实值连续初始函数向量，采样间隔定义为τ=tk+1-tk，A1、A2、B1、Dc、C、Dd、F分别为具有适当维数的常数矩阵。式(1)中，E和C应满足：

对于系统(1)，动态方程中可能存在奇异矩阵E，故在设计滤波器时计算其限制矩阵非常困难。因此，本文引入参数将其转化为非奇异系统。

引理2.1[3]若存在矩阵R1∈Ra×b，R2∈Rb×c，R∈Ra×c，其中R满足 r ank(R)=c，则322

的通解为：

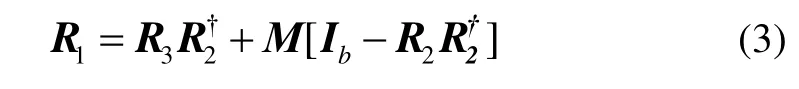
其中，Μ为任意矩阵，R2†表示R2的伪逆。

其中，［HG］由式(5)求解，

Γ∈Rn×(n+m)代表设计自由度。

由式(4)可知，对于任意x(t)，有式(6)成立：

对式(6)使用Euler离散化方法，则有：

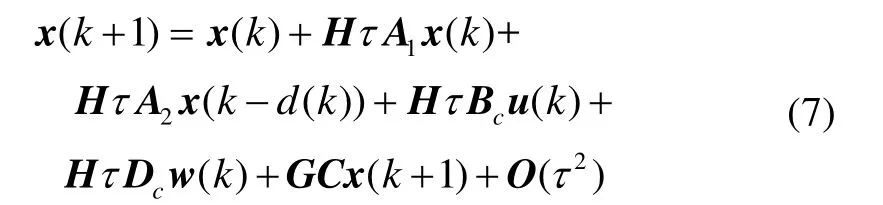
系统(1)中量测方程可表示为：

第三项可表示为：

其中，dM=τMτ。

联合式(7)～(9)，系统(1)可离散化为：

其中，A=τHA1+In，Ad=τA2，B=τBc，Bd=τDc。

定义：

则式(10)可重新表示为：

故而，系统(1)的传感器故障诊断问题可转化为系统(12)的传感器故障诊断问题。

注释1本文中采样间隔τ应充分小以保证Ο(τ2)忽略不计，采样间隔与时滞应满足：τ≤dm，d(k)满足0≤dm≤d(k)≤dM，dm=τmτ，dm和dM应为整数。

2 鲁棒传感器故障诊断滤波器设计

由于故障诊断包括残差生成和残差评价，故而，本节设计一个基于观测器的故障诊断滤波器作为残差生成器，使得：

其中，γ＞0，Wf为稳定加权矩阵，

注释2当Wf=I时，残差r为故障的H∞估计，即故障发生在全频域范围。为提高故障估计性能，提出加权矩阵Wf，式(13)代表Wf频域范围内的H∞估计。假设Wf有如下最小实现：

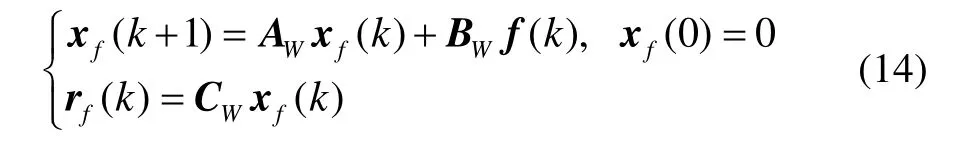
其中，xf∈Rnf，rf∈Rq，AW、BW、CW分别代表常数矩阵。

联合系统(12)和(14)可得如下增广系统：

其中，

对于增广系统(15)，其基于观测器的滤波器具有如下非奇异结构：

其中，∈ Rn为状态估计值，∈ Rm为滤波器输出，L∈R(n+nf)×m和V∈Rq×m为待设计的参数矩阵。

定义：

由式(17)及(18)可得：

其中，

由式(19)和(20)可得如下增广系统：

此时，不等式(13)可重新表示为：

本文设计的故障诊断滤波器应满足：

1）当(k)=0时，式(21)中动态方程应渐进稳定；

2）在零初始条件下，φ(k)=0，不等式(22)成立。

定理1若存在对称正定矩阵P∈R(n+nf)×(n+nf)，Q∈R(n+nf)×(n+nf)，Z∈R(n+nf)×(n+nf)，标量γ＞0，使得：

其中，

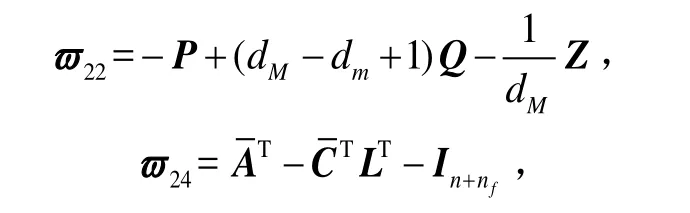
“*”代表对称矩阵中的对称元素，则当(k)=0时，增广系统(21)中动态方程渐进稳定。

证明：定义：

选取如下有关误差的Lyapunov-Krasovskii方程：

其中，

当(k)=0时，可得以下不等式：

其中，

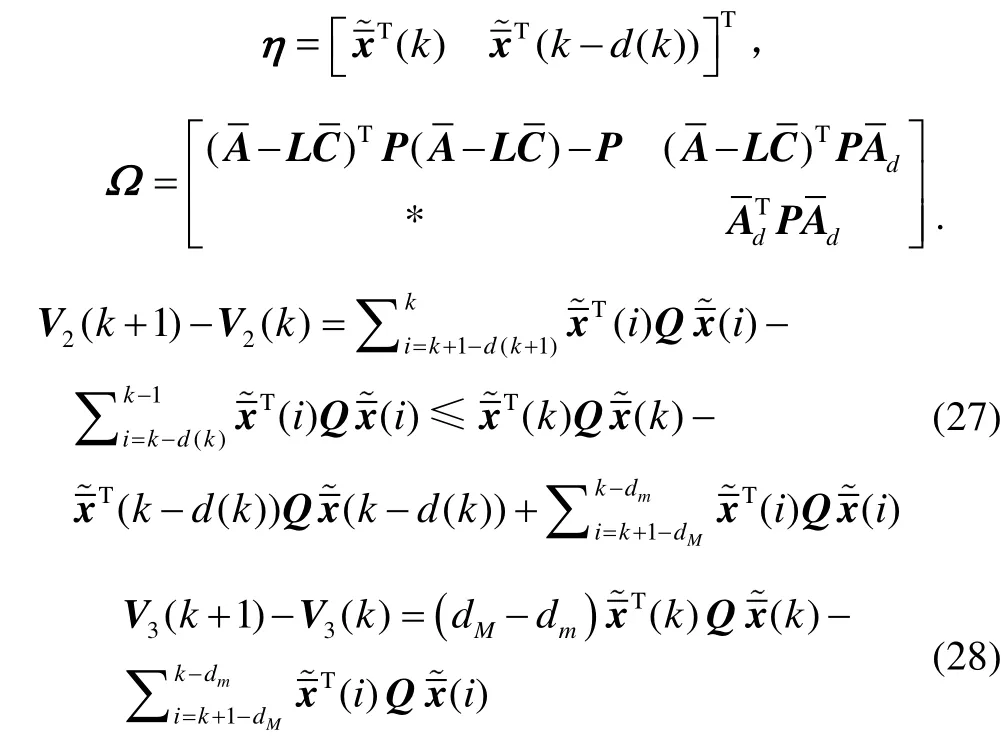
另外，由式(24)可得：

由式(29)可得：

由式(26)～(30)可得：

其中，

由Schur不等式可知，Θ＜0等价于：

对式(32)左乘 d iag(P-1,I,I,Z-1)及右乘其n+nfn+nf转置，则式(32)等价于式(23)。

由Θ＜0可知，存在充分小的正标量δ使得：

由式(31)和式(33)可得：

故，当w(k)=0时，(21)中动态方程是渐进稳定的，定理1得证。

注释3在不等式(23)中，由于存在P-1、Z-1，式(23)不是标准LMI。尽管如此，CCL算法能够有效解决该问题，其步骤可参照算法1。

定理2若存在对称正定矩阵P∈R(n+nf)×(n+nf)，标量γ＞0，使得不等式(35)成立，则当增广系统在零初始状态时，φ(k)=0，此时，对于任意非零的w(k)∈L2[0,+∞)，均有式(22)成立，其中，ϖ22=ϖ22，ϖ25=ϖ24。

证明：定义：

选取如式(25)所示Lyapunov-Krasovskii方程，则有：

其中，

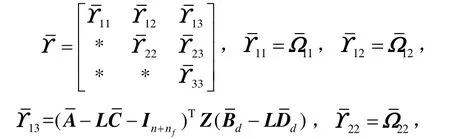
由式(27)(28)(37)(38)可得：

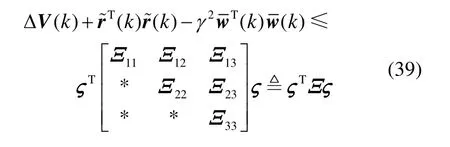
其中，

由Shcur补引理可知，Ξ＜0等价于式(40)：

由式(36)可得：

对式(41)两端从0到+∞相加则有：

已知当系统在零初始状态时，φ(k)=0，则有(k)=0，V(0)=0，又V(∞)＞0，故：

即，对于任意w(k) ≠ 0、w(k)∈L2[0,+∞)，均有不等式(22)成立，定理2得证。

注释4考虑式(35)(23)，容易发现若有式(35)成立，则必有式(23)成立，即若定理2成立，则性能指标(1)和(2)可同时满足，此时，设计的滤波器是线性时变时滞广义连续-离散系统的鲁棒H∞故障诊断滤波器。

为解决不等式(35)中由P-1、Z-1导致的非凸问题，本文引入CCL算法。

定义最大迭代次数为Kmax，满足式(44)(45)的γ初值为βmin，对于给定的时变时滞参数dm和dM，使用CCL算法求解式(35)中γ最小值，观测器参数矩阵L和V，其具体步骤如算法1所示。

算法1：

步骤1对于给定参数dm≥0，dM＞0，Kmax＞0，给定满足式(44)(45)的充分大的γ初值βmin，令βnim=γ。

步骤2寻找满足式(44)(45)的可行解L0、V0、P0、Q0、Z0，若不存在，退出；否则，令k=0并跳转至步骤3。

步骤3解决式如(44)(45)所示LMI问题：

及限制条件P＞0，Q＞0，Z＞0，寻找可行解L、V、P、Q、Z，令Pk+1=P，Zk+1=Z，W1k+1=W1，W2k+1=W2。

步骤4验证式(35)，若成立，令γmin=γ，减小γ值并跳转至步骤2。若式(35)不成立且k=Kmax，退出。否则，令k=k+1，并跳转至步骤3。

为尽早检测出故障，给出残差评价函数及阈值以判断故障是否发生。本文中，残差评价函数Jr及阈值Jth选择如下：

N表示残差评价函数时间窗的长度。在残差评价过程中，N的长度是有限的，这是因为故障应当尽早被检测出，在全时域范围内对残差进行评价没有实际意义。

基于式(47)(48)，可通过如下的残差判断逻辑，判断故障是否发生：

Jr＞Jth⇒故障⇒报警；Jr＞Jth⇒无故障发生。

3 仿真分析

本节给出时变时滞连续-离散描述系统模型以验证设计方案有效性。考虑如下小角度情况下卫星姿态控制模型[18]：

其中，ψ表示偏航角，φ表示滚动角，θ表示俯仰角，ωx、ωy、ωz表示三轴角速度，为控制力矩，T表示外部扰动，ω表d0示卫星绕中心引力体旋转的轨道角速度。

本文中，ω0取值为0.001 rad/s，量测信号为离散变量，姿态角度由星敏感器测量，角速度由陀螺仪测量。另外，J=diag(Jxx,Jyy,Jzz)表示转动惯量，其取值如表1所示。

表1 转动惯量参数Tab.1 Parameters of moment of inertia

令x=[ψ φ θ ωωω]T，u=T，xyzc y=[ψ φ θ ωωω]T，考虑系统时滞为 ：xyz d1(t)=0 .02 +0.01sint，τm=0.01s，τM=0.03s，若ωz为常值，即z=0，且陀螺发生故障，则由式(49)及(50)组成的系统可表示为形如式(1)的时变时滞连续-离散描述系统模型，其参数如下：

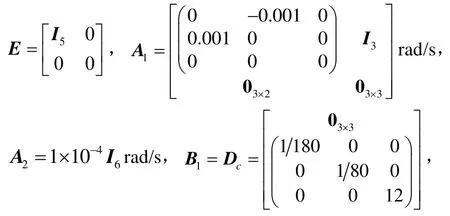
F=[0 0 0111]T，Dd=0，扰动w为均值为零的高斯白噪声，其标准差为 0 .05I3rad/s。

在式(5)中，选择Γ=[I606×6]，则H和G的取值分别为：

容易验证H非奇异，且H、G满足式(4)。

选择：Aw=-1，Bw=1，Cw=0.1。使用 CCL算法，则γ=1.18，求得的L和V值分别为：

V=［ 1.9300,-0 .8165,1.2605,-0 .4238,-2.0323,0.7211］.

其中，

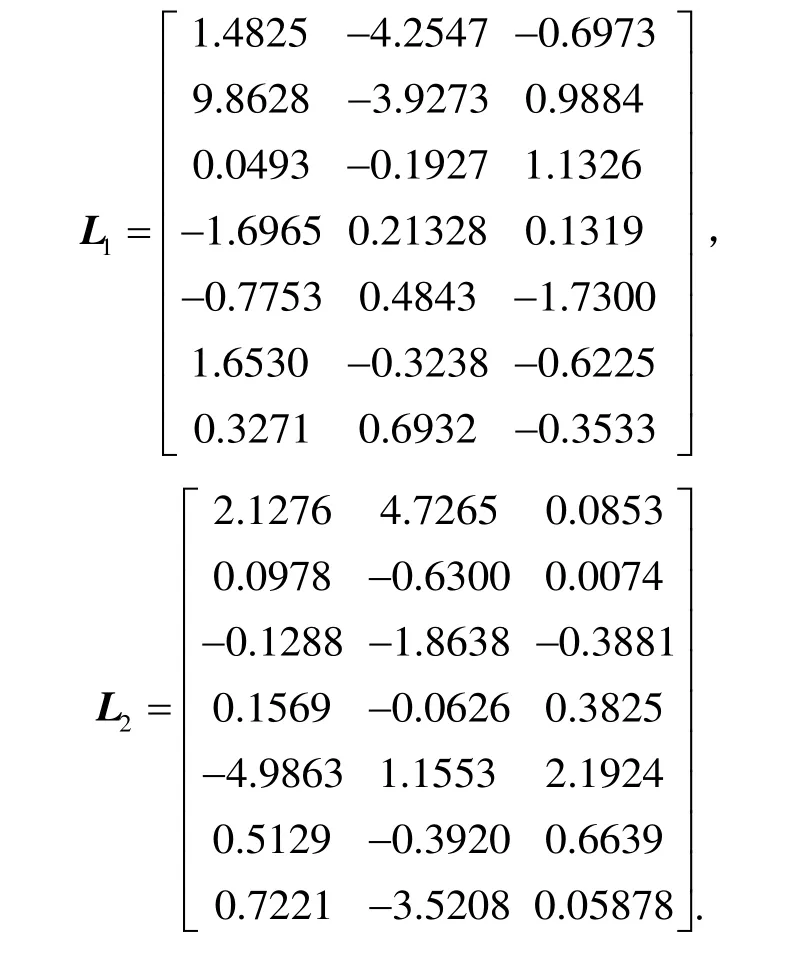
假设系统发生如下离散化后故障：

得到的故障诊断结果如图1～3所示，得到的故障估计均方根误差（RMSE）如表2所示。

图1 故障 f1及其估计Fig.1 f1 and its estimation

图2 故障 f 2及其估计Fig.2 f2 and its estimation

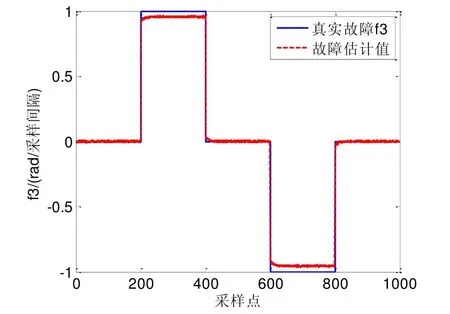
图3 故障 f 3及其估计Fig.3 f3 and its estimation

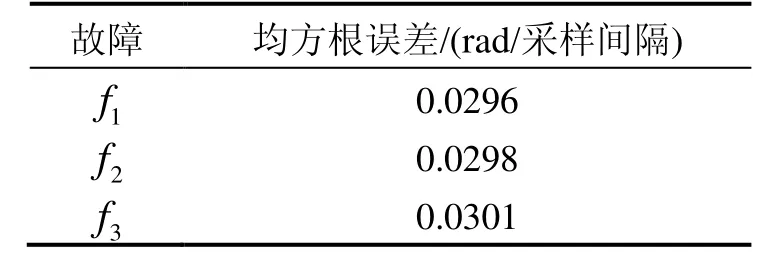
表2 f1至 f 3故障估计均方根误差（RMSE）Tab. 2 RMSEs of fault estimation for f1～f3

由图1～3可以看出，对于故障f1～f3，均可得到较好的故障诊断结果，表1进一步验证了该算法有效性。由表 1可知，对于故障f1～f3，故障估计误差均约为 0.03rad/采样间隔，表明设计的故障诊断滤波器能够执行有效的传感器故障诊断。

选择阈值为Jth=0.02。图4～6为残差评价函数图。当残差评价函数超过阈值时，故障可被检测出。

由图4～6可知，因选取了适当的残差评价函数及阈值，故障可以很轻易的被检测出。

最后，我们对设计的故障诊断滤波器的鲁棒H∞性能指标进行分析。参考文献[12]中有关内容，在本文中，增广残差与故障和增广扰动若满足

图4 故障 f 1残差评价函数Fig.4 Residual evaluation function of f1

图5 故障 f 2残差评价函数Fig.5 Residual evaluation function of f2

图6 故障 f 3残差评价函数Fig.6 Residual evaluation function of f3

则本文设计的故障诊断滤波器是鲁棒H∞故障诊断滤波器。

4 结 论

本文针对具有惯性测量元件的线性时变时滞连续-离散描述系统，设计了一种新的具有非奇异结构的基于观测器的故障诊断滤波器。首先将具有时变时滞的连续-离散描述系统转化为一般系统进行研究。设计的基于观测器量测残差的故障诊断滤波器符合鲁棒H∞性能指标。由于滤波器参数矩阵不等式不是标准LMI形式，引入CCL迭代算法以辅助运算。引入残差评价函数及阈值以判断故障是否发生。仿真结果表明，对于时变时滞连续-离散描述系统传感器发生的缓变故障和突变故障，本文设计的故障诊断滤波器均能实现有效的故障诊断。