以扰动重力为边值条件确定外部扰动重力场

田家磊，李新星，刘晓刚，冯进凯，范 雕

（1. 信息工程大学 地理空间信息学院，郑州 450001；2. 63850部队，吉林 白城 137000；3. 武汉大学 测绘学院，武汉 430079；4. 西安测绘研究所，西安 710054；5. 地理信息工程国家重点实验室，西安 710054；6. 大地测量与地球动力学国家重点实验室，武汉 430077）

地球重力场是地球的基本物理场，同时也是大地测量学、海洋学、地震学、国防科学、空间科学、地球物理学等学科重要的研究对象[1-2]。地球重力场及其时变反映了地球内部质量分布情况和运动状态，同时决定了大地水准面形状与随时间的变化[3-4]。物理大地测量学的两大基本任务就是确定地球的形状和地球外部扰动重力场[5]。

导弹、飞机、火箭、航天飞机、卫星、宇宙探测器等飞行器在飞行过程中都要受到地球外部重力场的影响，所以它们的发射、制导与控制等过程需要精确的重力场信息来提供这些运动物体力学的重力场约束[6]。随着惯性器件的精度越来越高，扰动重力场对惯性导航系统（INS）的影响越发地突出，想要进一步的提高导航精度就需要在导航的过程中对扰动重力进行补偿[7]，由此也加大了对高精度、高分辨率的扰动重力场模型的需求[8]。重力辅助导航也是近些年研究的热点之一[9]。

目前地球外部扰动重力场的模型构建和等效逼近理论主要包括两类：模型逼近和算法逼近。模型逼近主要有Sttokes理论和Molodensky理论等。算法逼近主要有贝亚哈马解、虚拟点质量解[10]、虚拟单层密度解、最小二乘配置解及球谐函数解等。虽然上述方法可以用来确定地球外部扰动重力场，但在应用上均受到一定的限制。

传统的重力测量及数据处理得到的是重力异常，经典的物理大地测量理论也都是以重力异常为边值条件。但是随着 GNSS、航空重力等技术的发展，高精度、高分辨率扰动重力数据的获取变得经济、便捷与高效。目前利用扰动重力确定区域大地水准面的研究比较热门，然而对于利用扰动重力构建扰动重力场的研究比较少。下面结合实际应用的需要，讨论利用扰动重力确定外部扰动重力三分量的方法。

1 格林积分法

球近似下地球各元素之间的几何关系如图1所示。

由位理论可得，扰动位T是调和函数，根据调和函数的性质，扰动位可由格林第三式表示为：

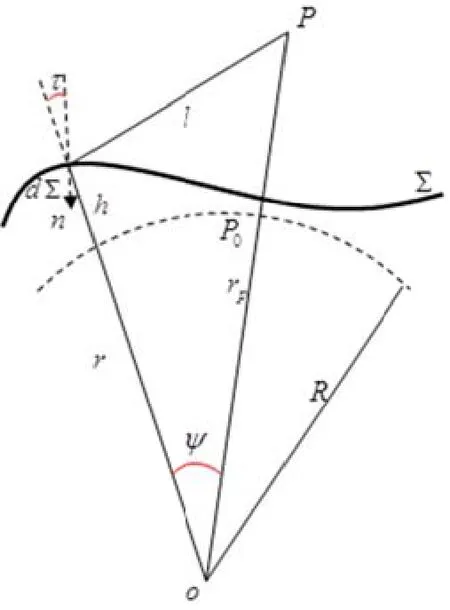
图1 球近似下各元素之间的几何关系Fig.1 Geometric relations among the elements under the condition of the ball approximation

式中，∑表示地面，d∑为地面上的面元，l是计算点p与面元的距离，n是相对于调和空间的边界面外法线方向。ψ为计算点p与地面∑上的面元d∑的球心角，∂T∂n和T分别表示地面的扰动重力和扰动位。式(1)就是应用格林公式以实际地球表面为边界面，以扰动位和扰动重力矢量为边值条件，计算外部扰动位的公式。它需要具有二者的观测值才能进行解算，地形复杂时法线方向的计算是比较困难，这两个因素限制了格林公式的实际应用。尽管如此，格林公式提供了一种以地球自然表面为边界面（自然表面上的扰动位与扰动重力矢量为边值），而不需对任何边值进行延拓或归算，确定地球外部扰动重力场的解析形式[11]。

实际应用中的地形与重力数据都是格网化的形式，通过分析与简化可以得到基于格网数字地形面的格林公式：

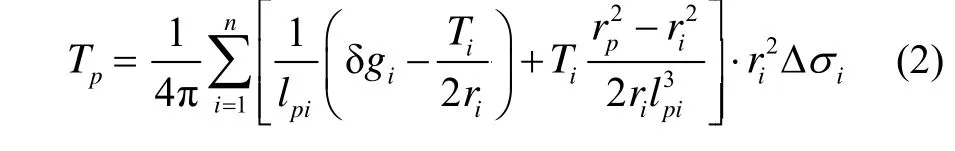
式中，δgi为积分点的扰动重力，lpi表示计算点与地面点之间的距离，Ti为地面点的扰动位，rrp和ri分别表示计算点和地面点的地心向径，Δσi=cosφi⋅ Δφi⋅Δλi为格网的单位球面积，λ、φ分别为经度和纬度。

式(2)表明利用格林公式求解地球外部扰动位同时需要有地面的扰动位以及扰动重力的垂直分量这两个边值条件。分析式(2)的形式可以看出它是由扰动重力垂直分量的单层位和扰动位的泊松核的位两部分组成。在球近似的情况下它们分别是这两种边值问题的解。对式(2)做一定的改进可得：

式中，p0是计算点沿着向径至地面上的点，Tp0表示p0点的扰动位，γ是正常重力，ζ是高程异常。

式(3)采用了相对于p0点的高程异常差作为输入数据，这样做的好处有：它消除了高程异常的系统性误差和长波长的误差，p0点附近高程异常差接近于零，降低了积分的奇异性，精度更高的扰动重力可以起到更大的作用。

地球外部扰动重力矢量通常采用沿球心向径、纬度和经度三个方向的分量表示。它们与扰动位有以下关系：

其中，Api是计算点p与流动面元之间的方位角。将式(3)带入式(4)得到：

利用式(5)，即可由地面上的扰动重力和相对0p的高程异常差计算出地面或空间一点的扰动重力矢量的三个分量。

2 豪汀积分法

第二边值问题是指根据边界面上调和函数的法线导数推求界面内或者界面外的调和函数的问题，亦称Neuman边值问题，球外部第二边值问题的解称为Hotine积分。

式中，δg为扰动重力，H(rp,ψpi)为Hotine核，具体形式为：离散化可得：

由式(4)可得：

根据图1所示的球近似下各元素之间的几何关系可得：

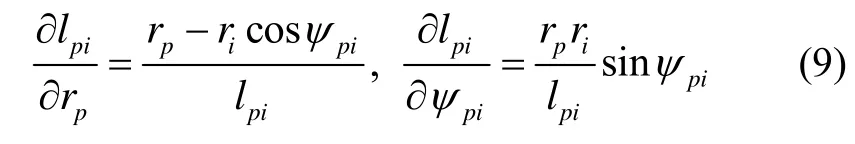
将式(9)带入式(8)可得由豪汀公式计算扰动重力三分量的公式：

3 点质量模型法

瑞典的地球物理学家贝亚哈马于 1964年提出的一种理论，其核心思想就是把地球对外部点的扰动位当成完全处于地球内部一个虚拟球（贝亚哈马球，见图2）对它的引力位。基于贝亚哈马理论，后来有学者提出用位于贝亚哈马球上面的虚拟单层位模型等效逼近地球外部重力场。单层位模型的积分核函数是空间距离的倒数，便于计算。若将虚拟单层质量离散化就可以得到虚拟点质量模型。

现假定点质量模型由分布于地球内部的k个扰动质量为Mj(j=1,2,…,k)的离散扰动质点组成。根据牛顿万有引力定律可以算出地球表面外任意一点P的扰动位，即

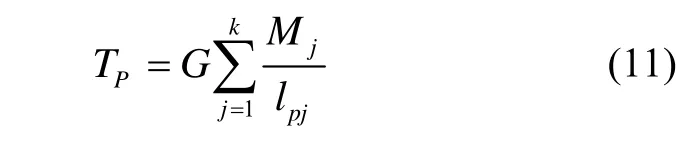
式中，G是引力常数。扰动重力场可以由埋藏在地球

图2 贝亚哈马球Fig.2 Bjerhammar sphere

式中，BR为贝亚哈马球的半径，δig为第i个扰动重力观测量。扰动质点的质量可以由地面上已知的扰动重力来推求。由式(12)可以推导出点质量模型计算扰动重力三分量的式：

4 扰动重力的向上延拓

扰动重力和扰动重力的径向分量数值相等方向相反，因此扰动重力的向上延拓是求扰动重力径向分量的实用方法。向上延拓属于第一边值问题，泊松积分是第一边值问题的解。对于调和函数的向上延拓的实用公式为：

rδg是调和函数，根据调和函数的性质得到关于扰动重力的向上延拓式：

式中，P是计算点，P0是P沿向径方向在球面上的投影点，Q为流动点。

5 实验与分析

下面采用2160阶EGM2008地球重力场模型模拟计算北纬 23.5°～28.5°，东经 111.5°～116.5°区域，大地高为 0、分辨率为2′×2′、大小为150×150的格网扰动重力和高程异常网格数据。空中数据采用2160阶EGM2008模型模拟计算北纬 24°～28°，东经 112°～116°区域，高度为3000 m和1500 m、分辨率为2′×2′、大小为120×120的格网扰动重力三分量，将其作为“真值”，检验各种方法计算外部扰动重力的精度。

采用同样的地面重力数据分别利用三种方法计算同样范围的扰动重力矢量然后和“真值”做差，结果统计如表1～6所示。

可以看出，随着计算高度的增加，三种方法的结果都变好，1500 m高度计算的结果点质量模型的精度是最好的，豪汀积分法次之但是其计算的径向分量结果不好，格林积分法的结果稍差。3000 m高度的水平分量计算结果豪汀积分法最好，格林积分法次之，点质量模型稍差，但是结果都比较好。相比另外两种方法点质量模型在两个高度的径向分量的计算都取得了较好的结果。

表1 格林积分法计算的3000 m高度扰动重力三分量差值Tab.1 Differences between true values and three components of disturbance gravity calculated by Green integral method at height of 3000 m

表2 豪汀积分法计算的3000 m高度扰动重力三分量差值Tab.2 Differences between true values and three components of disturbance gravity calculated by Hotine integral method at height of 3000 m

表3 点质量模型法计算的3000 m高度扰动重力三分量差值Tab.3 Differences between true values and three components of disturbance gravity calculated by Point mass method at height of 3000 m

表4 格林积分法计算的1500 m高度扰动重力三分量差值Tab.4 Differences between true values and three components of disturbance gravity calculated by Green integral method at height of 1500 m

表5 豪汀积分法计算的1500 m高度扰动重力三分量差值Tab.5 Differences between true values and three components of disturbance gravity calculated by Hotine integral method at height of 1500 m

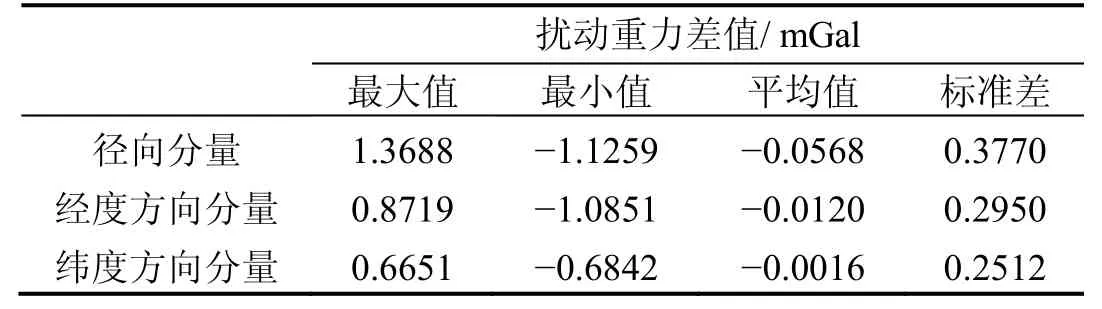
表6 点质量模型法计算的1500 m高度扰动重力三分量差值Tab.6 Differences between true values and three components of disturbance gravity calculated by Point mass method at height of 1500 m

为了研究扰动重力误差对计算扰动重力三分量的影响，并且实测的扰动重力数据由于观测条件的限制必然会有一定的误差，在原始数据加入3 mGal的高斯白噪声，然后计算扰动三分量差值，结果统计如表7～10所示。

从表 7～10可以看出，原始地面加入误差后，三种方法计算扰动重力三分量仍然取得了较好的效果，说明三种方法都有一定的抗差能力。同时利用向上延拓算法也可以很好地完成扰动重力径向分量的计算。

表7 格林积分法加入3 mGal误差计算的1500 m扰动重力三分量差值Tab.7 Differences between true values and three components of disturbance gravity calculated by Green integral method with 3mGal error added at the height of 1500 m

表8 豪汀积分法加入3 mGal误差计算的1500 m扰动重力三分量差值Tab.8 Differences between true values and three components of disturbance gravity calculated by Hotine integral method with 3mGal error added at the height of 1500 m

表9 点质量模型法加入3 mGal误差计算的1500 m扰动重力三分量差值Tab.9 Differences between true values and three components of disturbance gravity calculated by Point mass method with 3 mGal error added at the height of 1500 m

表10 向上延拓法计算扰动重力差值Tab.10 Differences between disturbance gravity calculated by upward continuation method

6 结 论

精确地确定地球的外部扰动重力场对提高惯性导航的精度愈发重要。随着GNSS技术的发展，重力测量以及数据处理中越来越广泛地采用大地高系统，因而获得了越来越多的扰动重力数据。本文研究了几种以扰动重力为边值条件确定地球外部扰动重力场的方法。经过实验说明三种方法都可以有效地计算扰动重力三分量。在低空领域点质量模型法与豪汀积分法（计算水平分量）加扰动重力的向上延拓（计算径向分量）的组合是比较好的方法。虽然在低空领域格林积分方法的结果稍差，但是其计算过程中不需要数据的归算，并且其核函数简单便于计算，在满足其条件的情况下也可以有效地确定地球的外部扰动重力场。