基于因子图的鲁棒性增量平滑算法的水面无人艇组合导航方法

戴海发，卞鸿巍，马 恒，王荣颖

（海军工程大学 电气工程学院，武汉 430033）

随着作战方式的变革，水面无人艇等（USV）智能化无人作战系统已成为现在及未来军事武器装备发展的主流趋势，并得到了世界各国的重视。与常规舰艇相比，水面无人艇具有小型、无人、反应快速、机动灵活、隐蔽性好、可长航等特点，适用于执行危险以及不适于载人船只执行的任务。

当前，水面无人艇的研制特点趋于小型化、低成本化和高精度化。在设计水面无人艇导航系统时，采用MEMS传感器可以大大降低系统的成本，同时减小无人艇的体积，然而MEMS传感器普遍精度较低，单独使用，无法实现高精度导航。为了提高水面无人艇导航系统的精度和可靠性，需要利用卫星导航系统、计程仪、天文导航系统等传感器来协助导航。这些传感器具有不同的误差特性，结合多种传感器的互补特性和余度信息能够提供比单个传感器更精确、更具鲁棒性的估计。但是这些传感器通常都按照不同的频率工作，并且输出信息有些是非线性测量值，给组合导航系统的设计增加了挑战。此外，水面无人艇在不同的任务和环境中，需要配置和可以使用的传感器种类并不完全相同，因此需要根据实际任务需求动态的改变组合导航系统中传感器的配置。

针对上述问题，传统的方法大多采用基于联邦卡尔曼滤波器的组合导航方法[1-3]。虽然这些方法能够通过数据同步处理方法[4]融合不同速率的传感器信息并实时计算出导航解，但是为了保持数据的同步往往需要丢弃一部分测量值，这样就会造成信息的浪费；同时，标准卡尔曼滤波器只能够解决线性问题，而大多数的传感器模型都包含非线性成分；至于扩展卡曼滤波器，由于边缘化了过去的状态而只使用了最近的状态估计，导致表示这些测量值的非线性因子在估计过程中不能够很好地重新线性化，因此该优化过程可能是概率不连续的，估计值并不是最优的。而UKF、PF等非线性滤波器由于计算量大，在工程上难以实现。此外，当某个传感器的信息出现故障变得不可用时，联邦滤波器需要进行较复杂的系统重构处理，而且该方法不支持新导航传感器的扩展。

文献[5-6]针对即时定位与构图问题，提出了一种基于因子图的导航传感器信息融合方法，该方法将信息融合问题用因子图模型来表示。因子图将未知变量结点和已知测量值的关系进行编码，融合来自不同的、可能非同步的传感器观测值的问题就变成在因子图中连接测量值定义的因子与相应结点的问题。使用因子图可以使系统具有即插即用的功能，当有新的传感器接入系统时，只需要在因子图中增加新的结点；同样的，当某个传感器由于信号丢失或者传感器故障变得不可用时，系统只需要限制增加相应的因子，而不需要特别的处理。但是该方法存在计算量大、延迟的问题。为此，文献[7]提出了一种基于因子图的增量平滑算法的信息融合方法，该方法只更新受新观测值影响的贝叶斯网络，避免了一些重复计算，极大地减少了计算量，达到了实时估计的要求。文献[8]将该方法应用到了 IMU/视觉/磁力计等机器人导航系统中，也取得了较好的效果。

对于水面无人艇的多传感器组合导航，经常会出现测量值异常的情况（比如GNSS接收机受到干扰或压制、多普勒计程仪无法探测到海底），这些异常测量值一般称为野值点。如果不对这些野值点进行处理，就会污染导航信息的融合结果，导致估计的导航状态精度下降。目前常用的鲁棒性方法包括传统的M估计和基于图优化的方法[9]，M 估计主要包括 Huber和Cauchy方法。基于图优化的方法包括可切换约束（Switch Constraint）、动态协方差尺度（Dynamic Covariance Scaling）以及最大混合（Max-mixtures）法，前两者适用于单峰高斯噪声分布，而后者适用于混合高斯分布。文献[9]通过试验证明了基于图优化的方法性能要略优于M估计的方法，此外，在图优化的方法中，可切换约束的方法性能最佳，但是计算量大。

本文针对上述问题，结合文献[7]的信息融合方法和文献[9]的可切换约束鲁棒性方法提出了一种新的基于因子图的水面无人艇组合导航方法。第1节阐述了组合导航系统的因子图表示方法；第2节推导了先验及常用传感器的因子表达式；第3节首先介绍了捆绑优化的原理，然后阐述了增量平滑算法的原理，最后针对异常测量值的问题，对切换约束的方法进行改进并应用到增量平滑算法中形成了基于因子图的鲁棒性增量平滑算法；第4节给出了实时的算法实现架构；第5节通过仿真环境试验分析比较了算法的性能，验证了所提算法的有效性。

1 组合导航系统的因子图模型

假设水面无人艇安装了一组输出频率不同步的传感器，其中包括产生高频率输出的IMU传感器以及输出频率相对较低的全球导航卫星系统（Global Navigation Satellite System,GNSS）、多普勒计程仪（Doppler Velocity Log,DVL）等。有些传感器在复杂环境下可能变得不可用，而另一些传感器只在特定情况下可用。组合导航的目的是通过融合所有可用的信息源计算出最有可能的导航解。

进一步假设x表示导航状态，包含水面无人艇的位置p、速度v和姿态ψ信息；c表示IMU的校正参数，包括加速度计和陀螺的零偏。令xi、ci分别表示时刻ti的导航状态和校正参数，定义直到当前时刻tk的一组全部导航状态和全部校正参数为：

假设Λk为直到当前时刻 tk的所有变量组：Λk={Xk,Ck}。

根据上述定义，联合概率分布函数为：

其中， Zk为直到当前时刻 tk接收到的所有观测值。

假设时刻 ti的观测值为 zi，则那么，待估计参数的最大后验估计为

根据文献[8]，联合概率分布式(2)可以因式分解成一个先验信息和独立过程以及测量模型。令 p(Λ0)表示所有的可用先验信息，则因式分解可写成：

根据文献[7]，上述因式分解可以表示成因子图模型。如图1所示，因子图是一种双边图，包含两种类型的结点（因子结点和变量结点），边表示因子结点和变量结点存在关系。图中的每个因子结点都可表示式(4)中的一个独立项，因此：

图1 包含多频率测量值的因子图：高频率的IMU测量值、以及低频率的GNSS、DVL测量值Fig.1 Factor graph representation with multi-frequency measurements: high-frequency IMU measurement,lower-frequency GNSS and DVL measurements

其中，d(.)表示代价函数。

对于高斯噪声分布，因子 fi满足如下形式：

特别地，表示测量模型的因子定义为：

式中，h(.)为非线性测量函数，zi为真实测量值。

因此，式(3)的最大后验估计问题变成了最小化下列非线性最小二乘函数的问题：

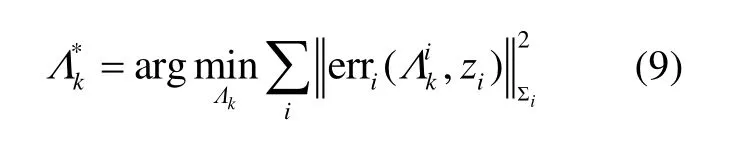
2 通用传感器的因子公式

从式(9)可知，因子 fi的推导是基于因子图融合方法的关键问题。本节将推导水面无人艇主要导航传感器测量模型的因子公式，这些传感器包括IMU、GNSS、DVL。

2.1 先验因子

可用的先验信息 p(Λ0)可以进一步分解为某些变量的独立信息，每一个独立信息可以表示成一个分离的先验因子。变量 υ ∈Λ0的先验因子是一个一元因子：

对于高斯分布，先验信息以均值μυ和方差Συ方式给出：

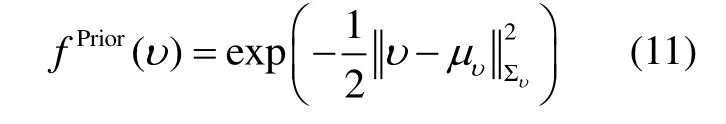
2.2 IMU等效因子

导航状态x 的随时间变化的关系可以描述成下述的非线性差分方程：

式中，h 为惯性导航系统的微分方程（参见文献[10]）；fb、ωb分别是惯性传感器测量得到的载体坐标系下的比力和角加速度；c表示IMU的校正参数，可根据IMU误差模型来修正IMU的测量值 fb和ωb。IMU的误差模型的估计通常与导航状态x 的估计结合在一起。线性化方程(12)将产生具有雅克比矩阵和过程噪声的状态方程。

通常，c随时间的变化关系可以用自身的非线性模型（即随机游走）来描述：

线性方程(12)(13)的离散化方程为：

根据同样的方法，可以得到IMU的偏差因子：

式中，ck+1和ck在因子图中表示为变量结点。

在实际中，考虑到导航应用的实时性，按照IMU的输出频率在因子图中增加新的因子来优化导航解并不可行。因此本文采用了文献[7]中的等效 IMU因子的更新策略，即根据预积分算法，将一系列连续的IMU测量值结合起来等效成一个IMU因子。

为了避免在重线性化的时候重新计算积分变化量，新的预积分算法采用了在预积分起始时刻ti所在的载体坐标系上进行积分计算的策略，同时为了避免欧拉角方法的奇异性问题，采用了文献[10]在流形上进行预积分的方法。

算法1：IMU测量值的预积分算法；先前的预积分变化量1）输入：IMU测量值、；校正参数；2）根据校正参数修正IMU的测量值；3）位置更新：；4）速度更新：；5）方位更新：的指数映射；6）输出：预积分变化量，其中 表示角速度向量为 .

等效IMU因子为

2.3 GNSS测量模型因子

一般的，GNSS测量方程可表示为：

该因子只与表示当前导航状态的结点xk有关。

当GNSS的测量值为伪距时，也可以按照同样的方法得到GNSS的因子表达式。

2.4 DVL测量模型因子

DVL通过声波的多普勒效应测量载体的对地或对水速度，如果测量值是对地速度，其测量方程可以表示成：

所以，DVL测量因子可以表示为：

如果测量值为对水速度，其测量方程可以表示成：

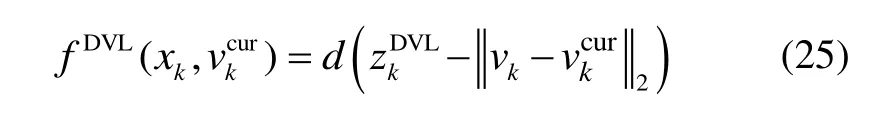
根据文献[4]，海流速度的变化模型可以用一阶Markov模型来描述：

式中，τcur为时间相关常数，ηcur为过程噪声。

海流模型的离散化方程为[17]：

式中，T为时间间隔。因此，水流速度因子可以表示为：

式中，hcur(⋅)为水流速度预测函数，即式(27)。

3 基于鲁棒性增量平滑的信息融合

3.1 捆绑优化

目前为止，信息融合问题已经使用因子图的表示方式推导出来，并且定义了一些常用传感器的因子。

因子图编码的非线性优化问题可以通过在标准高斯-牛顿非线性优化器中重复线性化来解决。从变量组Λk的一个初始估计值开始，高斯牛顿法通过线性化系统找到估计的修正值Δ满足：

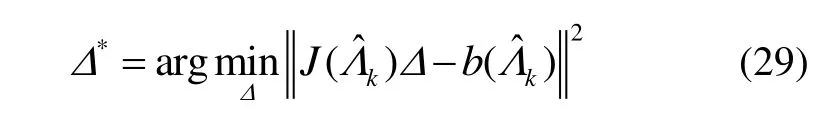
式(30)可通过矩阵求逆得到，但是当数据量较大时，计算量变得很大，因此一般利用矩阵分解来求解。假设矩阵J可QR分解为J=QR，则有QTJ=[R0]T且QTb=[dc]T，又根据式(30)，有RΔ=d。由于R为上三角矩阵，因此可通过回代法求得Δ。得到Δ后，线性化点更新到一个新的估计值

在因子图的框架中，该过程通过变量消除来完成[8]。首先确定变量消除的顺序，然后从因子图中依次消除各个变量，形成和弦贝叶斯网。在贝叶斯网络中，更新值Δ通过回代法得到，具体过程可参见文献[7]。

3.2 增量平滑

对于导航问题，系统每接收到一个新的传感器测量值就在图中产生一个新的因子。这等效于在线性化最小二乘问题的测量雅克比矩阵中增加新的一行，通常雅克比矩阵发生变化后，就需要从头对新的雅克比矩阵进行分解，但这样随着时间的增长计算量会越来越大。根据文献[8]，大部分的计算都和先前步骤是相同的，因此可以重复使用。当使用 3.1节的算法重新计算贝叶斯网络时，可以发现贝叶斯网络中只有很少一部分会因为新增加的因子而发生变化，因此并不需要每次都从头开始计算。

因此，当新的测量值到来时，只需要关注贝叶斯网络中受到影响的部分。一旦识别出贝叶斯网络中受到影响的部分，就将该部分转换回因子图的形式，并加上新的因子，然后将产生的因子图重新进行变量消除；再将变量消除得到的贝叶斯网络融合到原来未受影响的贝叶斯网络中，这样得到的结果与捆绑优化的结果是相同的。关于受到影响的贝叶斯网络识别算法，本文采用的是文献[7]提出的方法。

3.3 鲁棒性

为了提高因子图方法的鲁棒性，一般会采用可切换约束的方法。可切换约束的方法在2012年被提出用于SLAM中检测错误的闭环约束。后来，将其用来消除GNSS在城市环境中的多径效应[12]。文献[9]将代价函数修正如下：

式中，i表示1到k时刻之间的测量值序号，j表示残差未超过阈值的测量值序号，s∈{0,1}为切换约束变量，Sk表示到时刻k为止所有的约束变量，sj=0表示第j个测量值为正常值，否则为野值；γj为切换约束变量的初始估计，Ξ为切换约束变量的方差，ψ(sj)为实值函数且满足：

与普通因子图方法不同的是，该方法在对所有的状态量进行优化后，接着计算每一个测量值的残差，如果残差大于一定的阈值，则会在因子图中加入与该测量值相关的切换变量，然后重新优化，从而减轻野值点对优化结果的影响。具有可切换变量的因子图如图2所示。

图2 具有可切换约束的因子图Fig.2 Factor graph with switchable constraint

显然，由于上述方法需要进行两遍优化，因此计算量也成倍增加，不利于实时实现。针对上述问题，本文对该方法进行如下改进：

在将新测量值加入因子图之前，先对测量值做一个判断，如果测量值和预测值的残差小于阈值，则按照普通的因子图方法进行优化，否则，测量值可能是野值点，此时在因子图上增加一个与该测量值相关的可切换变量，使得该切换变量与状态量一起进行优化，这样就可以在一遍优化的过程中同时完成野值剔除和状态估计，从而减少了计算时间。

改进后的代价函数如式(31)所示：

式中，i*表示残差未超过阈值的测量值序号。

4 实时性能架构

尽管基于增量平滑的因子图融合算法的计算量要明显小于捆绑优化算法，但是融合一个新测量值的真实计算时间依赖于需要重复计算的贝叶斯网络规模。但是在实际应用中，需要实时的导航解。如果只处理IMU的数据，做到实时性是完全可能的；但是当外部传感器的信息到来时，处理时间尽管很小，实时性能还是难以保证。

为了解决这个问题，可以采用并行处理的方式。如算法1所示：当IMU的测量值在时刻到来时，采用高优先权的处理过程，根据算法 1预融合得到，然后通过、的估计值、以及预测函数实时解算出导航解；当非IMU数据在时间点到来时，可以采用低优先权的处理过程。该过程包括生成一个新的测量因子以及等效的IMU因子和偏差因子，这些因子和导航解以及校正结点、被加入到因子图中，根据预测函数初始化这些变量的估计值。特别地，的估计值通过预测函数产生；然后进入增量平滑算法，得到新的估计值，同时标记为新的预融合时间起始点，并且以为初始值；接着基于和实时计算导航解，其中k表示当前时间；一旦增量平滑完成，就用、的更新估计值替换和，且不需要修改。

算法2：实时性能架构1）初始化：新因子；2）初始化：根据先验因子，新变量、设置、，；3）while接收到测量值z时 do；4）if z是IMU 的测量值；5）通过算法1，根据z更新初始化；6）根据生成导航解；7）else；8）基于、以及，计算、的预测值、；9）为测量值z创建一个合适的因子；10）创建等效的IMU因子和偏差因子；11）增加因子；12）if 增量平滑可用；13）对于新的因子和变量结点、、到和，执行增量平滑算法；14）令；15）end if；16）初始化，；18）end if；19）if 增量平滑完成 then；20）重新更新最近的导航和校正参数结点的估计值x、c；21）令；17）令，，；

22）end if；23）end while.

5 仿真试验

本节中，利用仿真试验搭建一个 IMU/GNSS/DVL组合导航系统验证所提出的算法。共设计了两组试验：试验1设定所有的测量值都是正常值，然后通过与文献[6]的联邦卡尔曼滤波方法进行对比，验证本文算法的估计精度和收敛速度；试验2通过对测量值人为设置野值，与文献[14]的普通的基于因子图增量平滑方法以及文献[15]的切换约束方法进行了比较，验证算法的鲁棒性。

本文的算法是在开源库 gtsam的基础上修改实现，所有的方法都是在一台单核3.4GHz、16GB RAM内存的i7-6700处理器上完成的。

5.1 精度试验

利用Monte-Carlo仿真水面无人艇的运动，验证算法的可行性。首先创建了一条地面真实轨迹，仿真了水面无人艇以15m/s的速度航行。初始位置：纬度λ=108°，经度L=24°，海拔高度h=0m；初始航向为北向；仿真时间为400 s。轨迹包含几个匀速直行和大机动阶段，运动轨迹如图2所示，红色箭头表示水面无人艇航行方向。

基于地面真实轨迹，理想的IMU以100 Hz的速率产生测量值，同时考虑地球的自转以及重力矢量的变化。共做了100次Monte-Carlo仿真试验，其中每一次仿真中，这些测量值都加入了常值偏差和零均值白噪声。 加速度偏差标准差为σ=1mg，陀螺偏差标准差为σ=10(°)/h。加速度计和噪声方差的标准差分别为σ=100μg/，σ=0.1(°)/。初始位置误差为(10,10,10)m（东北天坐标系），初始速度误差标准差(0.5,0.5,0.5)m/s，初始姿态误差为(0.1,0.1,0.1)°。

此外，假设水面无人艇上装有北斗接收机、多普勒计程仪，测量量分别为位置和对地速度，并且分别以 1 Hz、2 Hz的速率发送信息。理想的北斗接收机的位置和多普勒计程仪的速度信息只包含噪声误差，假设为零均值高斯白噪声，误差标准差分别为σGNSS=20 m和σDVL=0.1 kn。

图3比较了纯惯性算法（Inertial）、基于卡尔曼滤波器的联邦算法（Federated Kalman Filter,FKF）以及本文提出的增量平滑算法（Incremental Smoothing,IS）的解算轨迹。从图3中可以看出，随着时间的增长，纯惯导解算结果误差不断积累，导致轨迹严重偏离真实轨迹，而采用组合导航修正惯性器件误差后，误差发散得到了抑制，估计结果与真实轨迹几乎吻合。

图3 真实轨迹与估计轨迹Fig.3 Ground real trajectory VS estimation trajectory

图4(a)～(e)比较了本文提出的信息融合方法与普通的联邦滤波方法的性能，这些性能分别为单次仿真的位置估计误差、速度估计误差、姿态估计误差、加速度计零偏估计、陀螺零偏估计误差。其中，IS表示本文提出的基于因子图的增量平滑算法的信息融合方法，FKF表示文献[6]提出的基于联邦滤波的方法。

从图4中可以看出，本文所提出的算法相对于卡尔曼滤波的方法对于所有的状态量都有更好的估计效果，加速度计与陀螺零偏估计误差接近于零。此外，由于基于因子图的增量平滑算法在完成估计的同时也进行平滑处理，因此该算法的估计误差更加平滑，且收敛速度也要快于传统的基于滤波的方法。

图4 增量平滑算法与联邦滤波算法的性能对比Fig.4 Comparison between incremental smoothing and federated filter

表1列出了100次蒙特卡洛仿真试验的各导航误差的估计均值和标准差。从表中可以看出，本文所提出的算法相对于卡尔曼滤波的方法对于所有的状态量都有更好的估计效果，位置估计误差从8 m减少到5 m以内，速度估计误差从0.15 m/s减少到0.10 m/s以内，姿态误差从0.4°减少到0.1°以内。

表1 100次蒙特卡洛仿真估计误差统计特性Tab.1 Statistics of estimation error in 100 Monte Carlo simulations

5.2 鲁棒性试验

在试验1的基础上，假定 GNSS接收机由于受到干扰导致其从 100～200 s的测量值变得不可用(出现大量野值点)，然后利用 3.3节提出的改进的具有切换约束的增量平滑方法（Modified Switch Factor-Incremental Smoothing,MSFIS）对 IMU、GNSS、DVL测量值进行融合。

表2列出了普通的增量平滑算法（IS）、具有切换约束的增量平滑算法（Switch Factor-Incremental Smoothing,SFIS），以及MSFIS方法的计算时间。从表2可以看出：SFIS方法的计算时间最长，超过了IS方法的两倍，这是由于SFIS方法增加约束因子而且进行了两遍优化；而 MSFIS方法虽然也增加了约束因子，但是它只做了一遍优化，因此计算时间仅比IS方法稍有增加，相比SFIS方法节约了大约56%的时间。

表2 三种因子图方法的计算时间Tab.2 Computation time of the three factor based methods

图5 几种基于因子图方法的平均定位误差Fig.5 Mean positioning errors for graph-based methods

图5为 100次 Monte-Carlo试验 IS、SFIS以及MSFIS三种方法的平均定位误差。从图中可以看出，由于野值点的影响，IS方法得到的优化结果严重偏离了真实状态，而后两种方法由于增加了约束因子，对野值点具有较好的鲁棒性。此外，从图中还可以看出，本文所提出的MSFIS方法与SFIS方法估计精度相当。综上可知，本文所提出的MSFIS方法对野值点具有较好的鲁棒性，而且显著的缩短了计算的时间。

6 结 论

本文提出了一种基于因子图的鲁棒性增量平滑算法的水面无人艇组合导航方法，该方法可以相对容易的对多传感器非同步测量数据进行实时融合，且可根据传感器的可用性实现即插即用的功能。本文所提出的方法，基于非线性优化的方法处理实时测量数据，并结合增量平滑的方法，实现了最小延迟条件下的近似最优估计。

通过 IMU/GNSS/DVL组合系统仿真环境对本文所提出的方法进行验证，并与传统的基于卡尔曼滤波器的联邦滤波算法及基于约束因子的鲁棒算法进行了性能对比。仿真试验表明，本文所提出的方法具有比传统基于滤波的方法更好的估计精度和更快的收敛速度；此外，该方法对野值点具有良好的鲁棒性，且计算时间要少于基于约束因子的鲁棒方法。由于篇幅限制，本文只推导了一些常用传感器的因子公式，并且假设测量噪声满足高斯分布，下一步将对更多传感器的因子公式以及非高斯测量噪声条件下的组合导航系统的融合方法进行深入研究。