三浮陀螺仪径向有源磁悬浮位置检测建模与优化设计

吴 辽，杨孟兴，王 卿，樊 理，申志刚

（中国航天科技集团 第十六研究所，西安 710100）

有源磁悬浮（AMB）应用于机电陀螺，改善陀螺浮子的支承状态，消除接触摩擦力，稳定浮子质心位置，可以直接提高陀螺零次项漂移和一次项漂移。对于精度达到万分级的陀螺来说，对浮子质心的稳定精度往往要求在纳米级，这就对陀螺浮子剩余质量的支承系统提出了更高要求。例如大量测试数据表明，对于动量矩约 200 kg⋅cm2/s的陀螺来说，测试时磁悬浮跳动0.02～0.05 μm，陀螺精度则很难优于10-3(°)/h。

AMB是制约三浮陀螺发展的技术瓶颈之一，建立准确、可靠的浮子位置检测系统是突破这一瓶颈先决条件。由于受空间尺寸限制，陀螺用磁悬浮必须设计成无位置传感器系统。近几年在这一领域的研究大部分集中在硬件电路、控制算法、磁悬浮干扰力矩等方面[1-3]，对电磁元件缺乏系统性的研究和设计，而常规的计算公式无法适应于三浮陀螺磁悬浮结构尺寸约束强、精度要求高、应用环境特殊等特点，计算所得误差较大[4-7]。与其他场合磁悬浮应用不同的是陀螺用的磁悬浮元件具有位置检测和位置调整的双重功能[4]，即磁悬浮元件既是位置信号传感器又是陀螺浮子位置调整的执行器。本文重点关注AMB的位置检测功能，首先推导建立了适用于外转子八极径向AMB的位置检测模型，并与实测数据进行对比分析验证，在此基础上对现有的磁悬浮元件结构方式进行优化，研究探索AMB在位置检测方面新的设计路径和方法。

1 磁悬浮系统

磁悬浮系统可分为三大部分，位置检测部分、中心处理电路和加力输出部分。元件部分一般由轴向元件、径向元件各两个协同完成位置信号敏感和加力动作执行[8]。系统工作在分时控制模式下，位置检测时元件的作用为位置传感器，浮子位置调整时元件充当执行器，系统框图如图1所示。

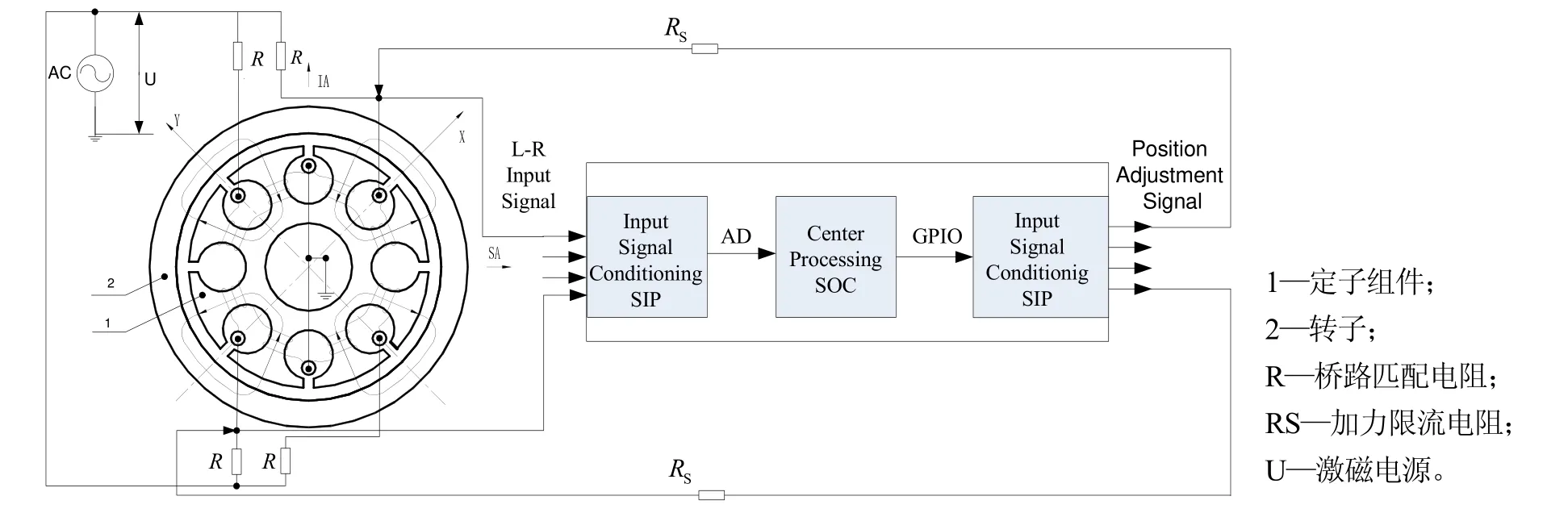
图1 径向AMB系统框图Fig.1 Radial magnetic bearing system

2 L-R敏感位置偏移量模型

从磁悬浮系统工作框图中不难看出径向磁悬浮位置检查机理为L-R惠更斯电桥。每个坐标方向由两个磁极组成，每个磁极配备一个绕组线圈。在位置检测周期时，电磁元件就相当于一个位置传感器，输入量为陀螺浮子的位置偏移量，输出量为桥路电压差。下面将对这一检测关系进行建模，并分析与灵敏度和线性度有关的因素[9-10]。

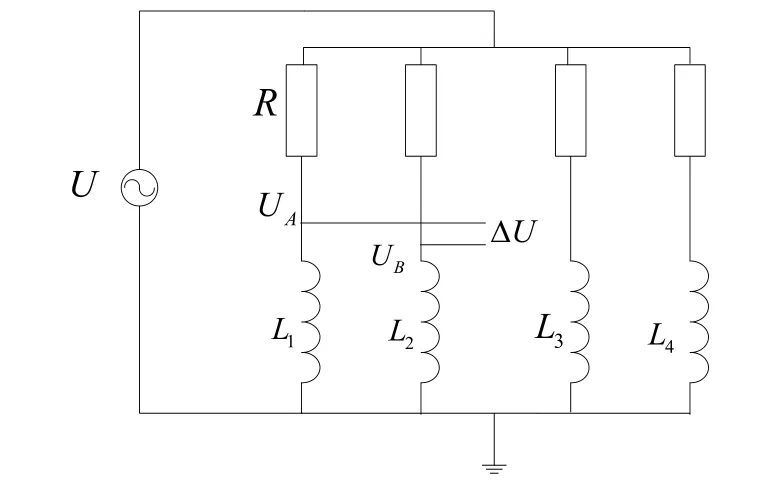
图2 径向磁悬浮位置检测原理电路Fig.2 Position detection principle circuit of radial magnetic bearing

如图2中所示，记桥路两端电压为UA、UB，

式中，L1、L2径向元件Y坐标方向的两组对称磁极下的电感，ω为激磁电源角频率。

对式(1)进一步计算可得：

为了便于化简计算，记X1=R/L1ω，X2=R/L2ω，且由于实际应用时选取的匹配电阻R使得UA、UB的测量值在560 mV左右，即R＜Lω，X1,X2＜1，因此有：

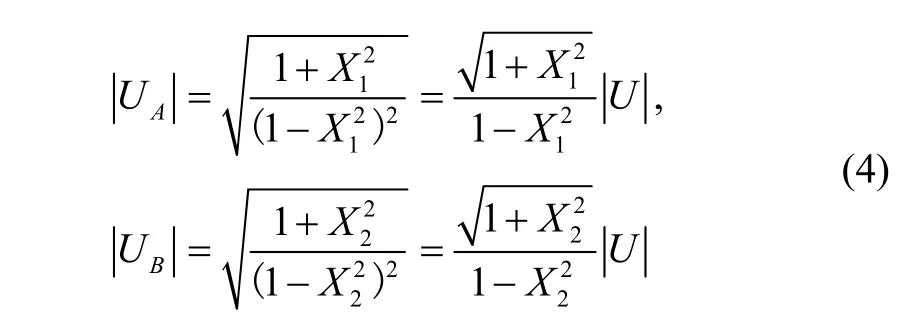
对于直接做差的后处理电路而言还需考虑桥路两端电压的相位，记为φA、φB：

由于目标值为ΔU=|UA|-|UB|，现需要对X1、X2中的关键量电感进行建模计算。径向磁悬浮元件单个坐标磁极模型接近于U型电磁铁，以此为基础建模再进行必要的修正。从安培环路定理入手，

式中，Hfe为铁芯气隙磁场强度；Ha为气隙磁场强度；s为工作气隙长度；lfe为铁芯磁路长度；N为绕组匝数；I为工作电流；μ0和μr分别为真空磁导率和铁芯相对磁导率。由于铁芯和气隙中的磁通密度B是相等的，式(6)中的Hfe和Ha进一步计算：

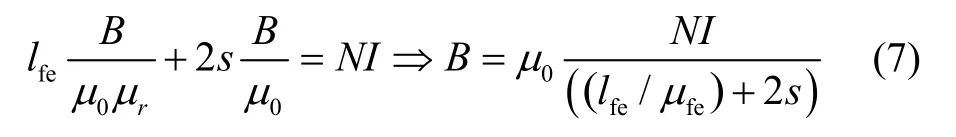
图3 U型电磁铁磁路Fig.3 U-type solenoid electromagnetic circuit

铁心中μr<<1，因此经常忽略铁芯的磁化作用，式(7)进一步简化为

电感L从线圈端点计算为L=NΦ/I，Φ为N匝线圈产生的全部磁通，

若要推导出适用于径向磁悬浮的电感计算公式，式(9)还需要进行修正：

式中，R1、R2分别为定子外径和转子外径，D为元件轴向长度，y为转子Y轴偏移量，因此式(9)可进一步写成：

式(4)与式(11)联立，并记|UA(B)|=F(X)，X=L(y)。直接化简式(4)较为困难，将其在y=0采用泰勒级数展开，并重点关注前两项，

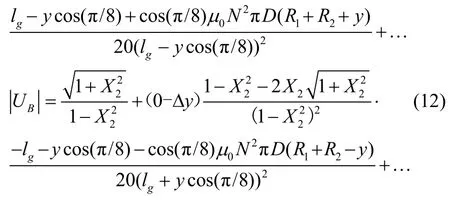
记y=0时，L1=L2=L0，X1=X2=X0，

在一定的简化推导后，建立了径向磁悬浮位置检测模型，进一步可以表示为 ΔU=k.Δy，k位置信号输出的灵敏度，

式(15)即给出了位置检测输出信号的灵敏度计算公式，常用单位mV/μm。

3 优化设计与实验验证

3.1 设计优化

磁悬浮元件在进行合格筛选测试时，元件输出信号的灵敏度和线性度是重要的两个参数，一般要求在[-15,15]μm范围内灵敏度不低于14 mV/μm，线性度误差小于10%。式(1)～(15)是本文给出的设计计算依据，可以进行设计校核。将采用公式计算的结果与实测数据进行对比，如图4所示。表1为原状态三个批次的实测统计值。从图4中可以看出，计算值与实测值在[-15,15]μm范围左右偏差很小，通过对实测值进行最小二乘拟合所得斜率值为15.15 mV/μm，与式(15)的计算值15.84 mV/μm偏差约为4.6%。该偏差由于在建模过程中进行了部分条件简化，忽略了铁芯磁化作用，泰勒级数展开后忽略二次项及高次项，认为转子处于机械中心时Y轴两个零位电感对称相等，这些都是计算误差的来源，也是生产过程中需要进行质量控制的地方。

基于前面的分析与验证在不改变现有产品的接口尺寸的前提下进行设计优化。对设计参数匝数N、定子外径R2、工作间隙lg、铁芯轴向尺寸D进行组合计算给出三种方案，如表2所示。输出结果如图5所示。

通过对图5量化对比分析，重点关注位置偏移量[-15,15]μm范围内的输出灵敏度和非线性误差。与原方案对比：方案一灵敏度提高23%，非线性误差降低16.3%；方案二非线性误差较大；方案三灵敏度较低。各方案对比结果见表 2。因此从位置检测角度来看，方案一优于其他方案。

图4 计算值与实测值对比Fig.4 Calculated value and measured valve

表1 灵敏度实测值统计Tab.1 Statistics ofsensitivity measurements

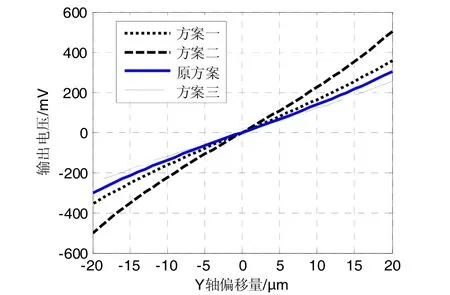
图5 各方案输出特性Fig.5 Output characteristics of eaach scheme

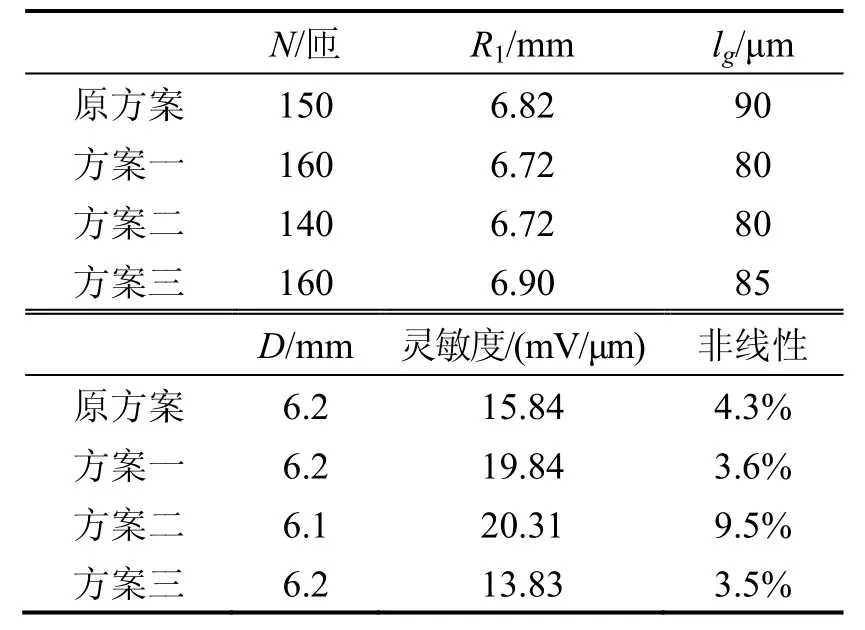
表2 方案优化对比Tab.2 Comparison on optimizatio n schemes

3.2 实验验证

前文已通过元件标定测试验证了所建模型的正确性，还需通过电磁仿真软件Flux对优化方案的力学性能进行校核，以及通过陀螺整表精度测试验证AMB的控制效果。力学性能仿真所建三维电磁模型如图6所示。

如图7所示方案一的仿真结果与原方案相接近，且在工作点60 mA电流附近输出电磁力学性能有所提升。以上计算和仿真结果表明，基于本文的计算方法给出的优化方案，有效地提高径向磁悬浮的位置检测质量和力学性能指标。

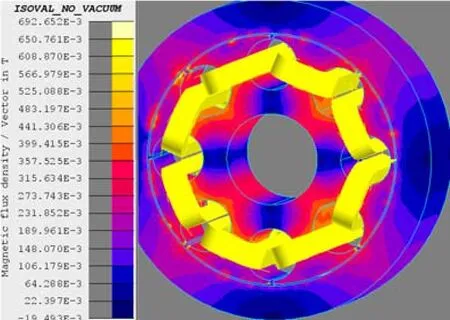
图6 径向元件磁场仿真模型（方案一）Fig.6 Simulation modell of radial component magnetic field(Option one)

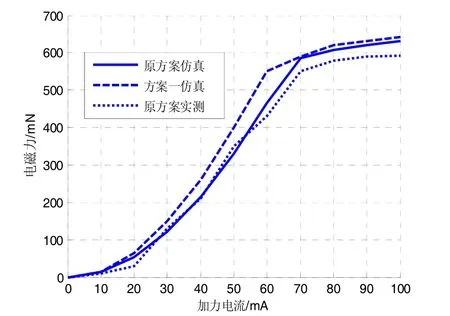
图7 不同电流产生的电磁力Fig.7 MMagnetic force oof different currr ents

AMB控制硬件采用16位A/D对交流转直流后的差分信号进行采集，检测范围00～～10 V，通过提高元件本身的设计灵敏度和抗干扰能力使得系统检测的有效精度从00.015 μm 提高至 0.01 μm。前后测试结果对比见图8。

陀螺固定位置漂移对浮子跳动最为敏感，以 OA轴固定位置精度测试为例，AAMB优化前后陀螺输出对比如图9所示。同时对陀螺做了不同姿态下的固定位置22 h漂移测试，每个方向测试三次，统计结果见表3。

从测试结果来看，图8中磁悬浮信号的跳动幅度有所减小，图9中陀螺输出尖峰得到了一定的抑制，这些均与AMB的控制优化有关。从表3中可以看出，优化后的AMB系统对陀螺在输出轴（OAA）和马达轴（SA）向上姿态下的精度平均提高 30%～50%。在输入轴（IA）向上姿态下基本没有改善，主要原因是陀螺IA方向输出存在斜率，跳动不是其主要矛盾。

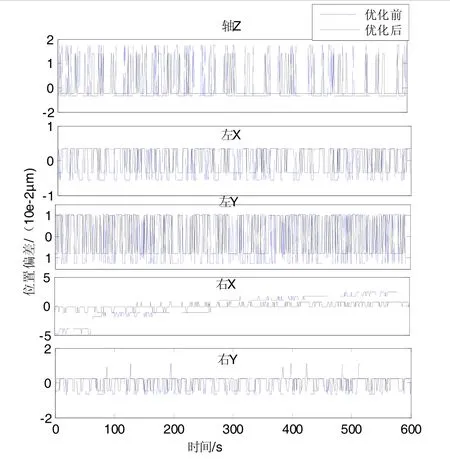
图8 优化前后磁悬浮位置信号对比Fig.8 Optimized before and after the magnetic levitation position signal contrast

图9 优化前后陀螺输出对比Fig.9 Optimized before and after gyro output contrast

表3 优化前后陀螺固定位置测试Tab.3 Optimization before and after fixed state drift rate of gyroscope

综上所述，优化设计后的磁悬浮元件有效地提高了元件位置检测灵敏度和线性度，优化控制算法削弱了陀螺输出尖峰的幅度，提高了陀螺精度。

4 总 结

合理优化AMB系统，为陀螺浮子提供高精度、低干扰的支承环境是提高三浮陀螺精度的关键。本文从三浮陀螺磁悬浮位置检测原理出发，推导建立了适用于八极外转子结构形式的径向磁悬浮位置检测数学模型，并通过测试验证了模型的正确性。

基于本文给出的模型和优化设计方法对现有磁悬浮元件结构方式进行了优化，使元件位置检测灵敏度提高了23%，非线性误差降低了16.3%，结合控制算法对AMB系统进行了优化。实验结果表明，优化后径向磁悬浮输出力学性能有所提升，陀螺固定位置漂移在OA轴向上和SA轴向上姿态下减小30%～50%，即本文提出的优化设计方法能有效改善AMB系统品质以及提高陀螺固定位置精度。