基于参数激励的MEMS陀螺电馈通抑制方法

赵鹤鸣，郑 奋，程梦梦，徐大诚，郭述文

（苏州大学 微纳传感技术研究中心，苏州 215100）

硅微陀螺仪是基于科氏效应测量目标物旋转角度或角速度的传感器[1]。陀螺工作时，包含两个振动模态，即驱动模态和敏感模态。通过科氏效应，实现两个模态间的能量转换。理论上，硅微陀螺仪的对称性使其驱动模态和敏感模态具有相同的谐振频率，通常采用与谐振频率同频的驱动激励信号对谐振子进行振动激励。然而在实际情况下，由于工艺、材料等方面的不可抗因素，硅微陀螺仪的对称性并非能够达到理想值，使用该方法时会引起从驱动模态到检测模态的耦合效应[2]，同时也会产生误差信号。除此之外，电路中存在的一些寄生电容，会导致陀螺驱动端的信号串扰到检测端。这种电馈通效应[3]造成的误差信号会严重影响陀螺检测模态的输出信号。由于这些局限性的存在，研究者们不断寻找可以提高陀螺仪各项性能[4]的解决方案。

参数激励法是一种抑制上述电馈通干扰的方法，在驱动模态中加入参数激励信号可以改变驱动模态中的刚度系数，使谐振系统达到谐振状态的一种驱动方式。1986年，Burdess[5]将参数激励法应用于球形谐振器上，最近十几年里才开始对 MEMS谐振器进行应用。美国哥伦比亚大学将参数激励法应用于音叉式陀螺仪，美国斯坦福大学[7]将参数激励法应用于高Q高频率的盘式谐振陀螺仪，并提高了敏感模态的灵敏度。较之国外研究，国内清华大学、上海交通大学等[7]也对参数激励法应用在硅微陀螺仪上进行了研究，虽然对改善陀螺性能也做了一定的工作，但比较系统和全面地将参数激励法应用于驱动模态下来提高陀螺系统性能指标的研究相对较少。

本文以硅微轴对称陀螺为研究对象，通过调制静电刚度的方式，使得在陀螺驱动响应不变的情况下，降低陀螺驱动激励的静电驱动力信号幅度，以此降低驱动信号对敏感检测的干扰。在文献[8]的基础上，利用多通道锁相放大器仪器，将参数激励信号添加到驱动激励中，并对该陀螺进行了性能测试。

1 硅微陀螺仪基本工作原理

1.1 动力学方程及能量传递方程

在理想状态下，硅微陀螺仪在驱动和检测方向上工作相互隔离互不影响，均可以用一个“弹簧—质量块—阻尼”二阶ks线性系统[9]来研究。硅微陀螺仪的理想力学简化模型如图1所示。

图1 硅微陀螺仪理想力学简化模型示意图Fig.1 Schematic diagram of ideal simplified mechanical model of silicon micro-gyroscope

硅微陀螺仪的基本动力学方程在时域上可以用一个常系数非齐次二阶微分方程表示：

式中，md、ms是陀螺驱动模态和检测模态的等效质量，cd、cs是等效阻尼系数，kd、ks是等效弹性系数，F(t)为外加驱动力，2msΩx是MEMS陀螺仪沿驱动方向振动时在敏感方向上产生的科氏力。驱动模态和检测模态的动力学方程仅与质量、阻尼、刚度这三个参数有关。

图2为硅微环式陀螺简化后结构图，其中，圆环外部分布16个电极，每个电极的弧长为2α，电极与圆环的初始间距是h0。

图2 环式陀螺简化结构图Fig.2 Simplified structure diagram of ring gyro

用u表示任意φ角度位置对应的环的振动位移[10]，

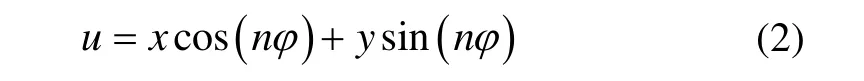
其中，x、y分别表示驱动模态和检测模态的振动位移。环与电极间的距离为h=h0-u，陀螺仪所具有的能量储存在环与电极之间，其能量表达式及其泰勒展开式如下：

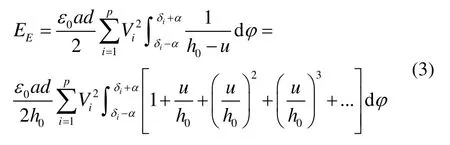
式中，δi代表第i个电极的中心角度，Vi是第i个电极和环间的电压差值，a是环的半径，d是环的厚度。由于环的位移u远远小于环与电极之间的间距h0，可省略式(3)中(u/h0)3及以上的高阶项并将其对x求导，得到电极板上总静电力为

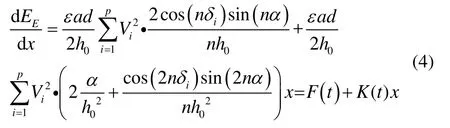
由此可知，电极板上的总静电力由两部分组成，F（t）为驱动力，K（t）x为静电刚度力。所以，驱动力F（t）和静电刚度K（t）的表达式可以写成如下形式：

1.2 电馈通效应

通常将输入信号与输出信号之间产生的静电耦合称为电馈通。电馈通的存在将影响陀螺仪零速率时的输出，从而干扰陀螺仪的正常运动，是陀螺仪角速率测量的误差源之一[11]。

目前已经有许多减小电馈通的方法，如减小驱动电压中的交流分量的幅度，使用专门设计的测量配置，消除寄生电容的影响，或者将陀螺仪的激励和运动的检测在时间上分开[12]。

本文采用的参数激励法是在驱动端新增一个频率为驱动激励信号频率两倍的参数激励信号，与驱动激励信号一起对陀螺进行激励。此时，陀螺输出的除了敏感检测信号以外，还会存在由于电馈通引起的干扰信号和参数激励信号。然后利用一个低通滤波器将二倍的参数激励信号滤除。由于参数激励法可以降低驱动激励信号的幅度，所以检测端得到的干扰信号远比未加参数激励信号前的干扰信号小，可以达到减小电馈通的目的。

2 参数激励法理论

参数激励法是一种改变方程中时变系数的激励方法。该方案中设置参数激励信号的频率为原始激励信号频率的两倍，谐振结构的刚度随之发生变化，通过控制系统调节参数激励信号的幅值，从而改变谐振结构的振动状态，达到谐振结构的振动控制[13]。采用参数激励法时，由于谐振子的振动幅度不受参数激励信号大小的限制，因此可以在不增加控制电路复杂度和不改变陀螺结构的前提下，通过刚度调制的方式，实现驱动输出与激励的增益放大。这样，就使得在驱动激励信号幅值下降的同时，仍能保持陀螺仪的响应不发生改变，从而抑制从驱动端到检测端产生的电馈通效应，改善零偏稳定性，提高陀螺的精度。在这里，当谐振器的刚度周期性地发生变化时，驱动模态的运动方程可以由Mathieu-Hill方程[14]表示。

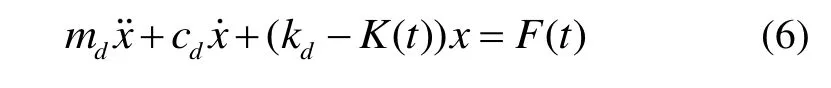
通过1.2节的推导，针对模态间能量传递问题，可推导出包含参数激励信号在内的系统运动方程。

将参数激励信号引入陀螺驱动模态，则驱动激励信号可由两部分构成[13]：

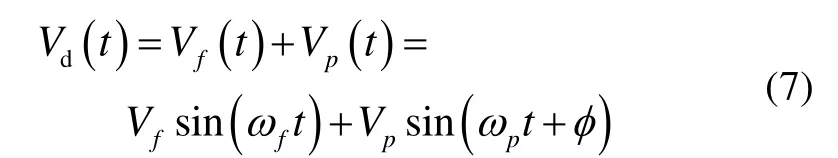
Vfsin(ωft)为原始激励信号，把Vps in(ωpt+φ)称为参数激励信号，同时，有ωp=2ωf。把驱动激励信号式(8)代入式(6)，可求得添加参数激励信号后的驱动力和刚度，即：

将解得的驱动力和刚度代入刚度调制后的陀螺仪动力学方程式(7)中，即可得到环式陀螺刚度信号发生周期变化的参数激励方程：

其中，

式中，α代表陀螺半电极的弧长，d是陀螺的厚度，Vdc是陀螺的直流偏置电压。根据陀螺仪结构参数，方程(9)的稳态解可以写成如下形式[15]：

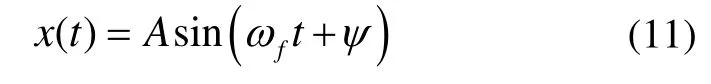
其中，

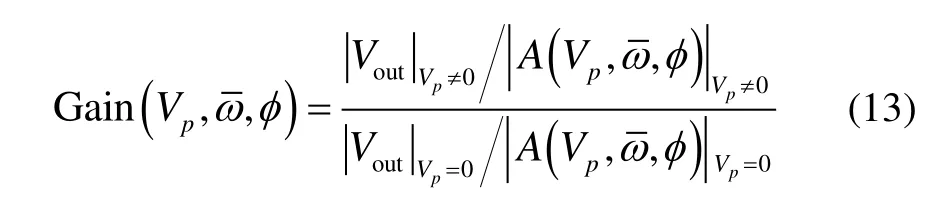
当系统处于谐振状态时，设φ=0，增益的最大值表达如下：

从式(14)可以看出，随着参数激励信号幅值的增加，驱动输出与激励的放大增益也越大。

3 实验过程与结果分析

3.1 十六边形环式陀螺结构

在本次实验中，以十六边形环式陀螺进行实验，结构示意图及其二阶振型如图3所示。其框架结构完全对称，谐振器由14个同轴十六边形环组成，通过8根交替辐条连接，并最终与中心锚点相连；质量块悬挂在环和辐条间的所有层上；最外环外侧是16个外部电极。

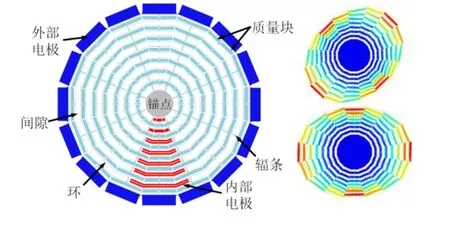
图3 十六边形环式陀螺结构示意图及其二阶振型图Fig.3 Schematic of hexagon ring gyro structure and its second-order mode diagram

陀螺的系统参数如表1所示。

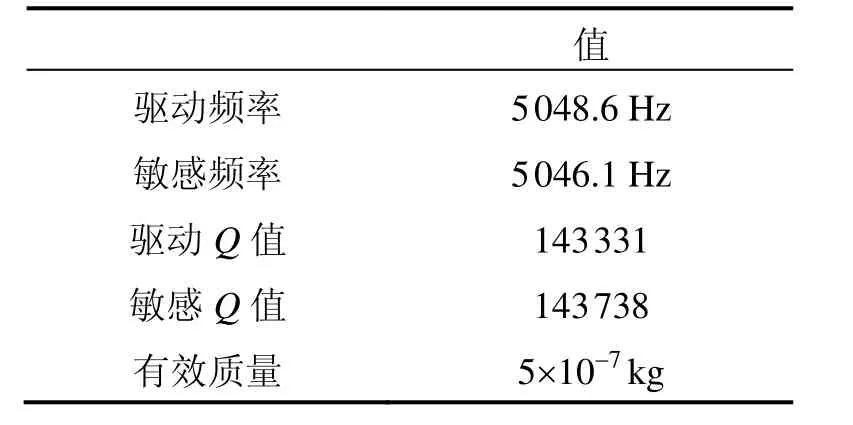
表1 十六边形环式陀螺系统参数Tab.1 Parameters of hexagon ring gyro system

陀螺的驱动模态框图如图4所示，驱动控制回路通过锁相环（PLL）和自动增益控制（AGC）保持驱动模态的频率和幅度恒定。在PLL控制中新增一个压控振荡器（VCO）模块，用于输出稳幅的二倍谐振频率激励信号，此信号即为参数激励信号。将其与驱动激励信号一同对驱动激励电极进行激励。

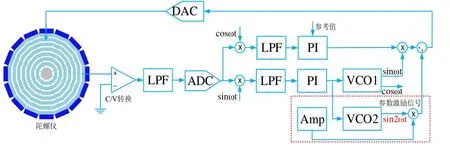
图4 十六边形环式陀螺驱动模态框图Fig.4 Block diagram of drive mode of hexagon ring gyro

3.2 实验过程

为了验证参数激励法在实际系统中的效果，在多通道锁相放大器上进行了实验。

多通道锁相放大器是瑞士苏黎世仪器公司研发的一款高频、双通道数字锁相放大器，具备多个输入输出接口、USB接口和电源等。实验设备及其连线如图5所示。

图5 实验操作图Fig.5 Experimental operation

在该仪器上实现的基于参数激励法的陀螺驱动闭环控制系统框图如图6所示，其中PLL 模块实现锁相环，PI模块实现自动增益控制[16]。

图6 参数激励法下的驱动环路结构图Fig.6 Drive loop structure diagram based on parametric excitation method

PLL模块主要由乘法器、低通滤波器、PI控制器以及数控振荡器组成。首先，仪器的解调器模块可完成乘法器和低通滤波器这两步骤的工作，将输入信号与振荡器输出信号相乘进行解调，经过低通滤波器滤除输出的高频信号保留低频相位信息，输入到PI控制器中。PI控制器调节相位信息，输出合适的控制信号，数控振荡器根据输入的控制信号输出相应的振荡频率。实验时需手动设置PLL 模块中数控振荡器的中心频率、扫频范围、陀螺谐振处的相位、低通滤波器的截止频率以及PI参数。由于使用了参数激励法进行实验，在实际操作中，新引入一路数控振荡器，其输出信号频率是原驱动信号频率的两倍，且与驱动信号同相。最后，将参数激励信号与驱动激励相加，所得的频率信号为最终控制频率信号。在本次实验PLL参数设置中，谐振器的中心频率设为5048.6 Hz，谐振点处相位是82°。

AGC环路系统主要由幅值解调、低通滤波、幅值比较和PI控制器组成。首先，在PI模块中设置控制驱动模态振动幅度的参考值和P、I参数。信号在输入PI模块之前经解调器模块进行乘法解调和低通滤波得到输入信号的幅度信息，将其与PI模块中设置的参考值比较得到幅值偏差信号，经PI控制器形成幅值控制量，即幅值增益，作为交流驱动信号的增益。最后，输出信号经仪器的输出端口与陀螺驱动模态的激励电极相连，实现幅度控制闭环。在本次实验 AGC参数设置中，PI模块中的参考幅度设为300 mV。

3.3 结果分析

首先，不添加参数激励信号，直接对D40号陀螺进行驱动闭环实验，驱动响应幅度锁定在300 mV。参数激励信号对驱动激励及增益变化趋势的影响如图7所示。可以看到未加参数激励信号前，驱动激励信号幅度为34.9 mV；逐渐增加参数激励信号，驱动激励信号幅度Vf逐渐下降；当参数激励信号幅度Vp加至185 mV时，驱动激励信号幅度变为 20.39 mV，驱动模态的幅度增益从最初的8.6上升至14.7。在无角速度输入时，敏感模态输出为电馈通信号，参数激励信号对电馈通信号的影响如图8所示，电馈通信号幅度为141.25 mV；增加参数激励信号后，电馈通信号幅度为 38.75 mV。由此可见，参数激励对减小电馈通干扰有很大的效果。

在常温下，在施加185 mV参数激励信号时，采集陀螺零偏输出40 min的数据，对其进行Allan方差分析，如图9所示，并将所测陀螺的测试结果汇总于表2。从表2可以发现，相比于未加参数激励信号的条件下，陀螺的零偏不稳定性从 6.864(°)/h降至4.316(°)/h，零偏稳定性从86.1972(°)/h降至26.5229(°)/h，性能分别提高了1.6倍和3.3倍。由于在系统中加入了参数激励信号，导致驱动激励信号的幅值下降，从而减少了电极内部的馈通干扰，进而降低了敏感模态检测输出中的噪声，提高了输出稳定性。

图7 参数激励信号对驱动激励信号及增益变化趋势的影响Fig.7 Influence of parametric excitation signal on driving excitation signal and gain variation trend

图8 参数激励信号对电馈通信号的影响Fig.8 Influence of parameter excitation signal on electrical feed-through signal

表2 D40号陀螺测试结果Tab.2 Test results of D40 gyro

图9 Allan方差曲线对比图Fig.9 Comparison on Allan variance curves

4 结 论

本文在PLL-AGC陀螺驱动回路中加入参数激励信号，实现了在不改变陀螺驱动响应情况下，减小了陀螺驱动激励幅度，达到提升陀螺性能的目的。实验结果表明，当参数激励信号加至185 mV时，可以将驱动激励降低近一半，且驱动模态的增益提高了近一倍。同时，对陀螺敏感模态进行开环实验，通过检测陀螺的零偏，表明参数激励法可有效降低了陀螺的零偏不稳定性，提高陀螺输出信号的稳定性。