重视几何直观 培养数学素养

胡萌

[摘 要]几何直观是学好数学的有利工具，也是提高数学素养的重要工具。培养学生的何直观能力作为教学的重要任务，应受到教师的重视。教师可通过引导学生利用图形描述概念或问题，培养几何直观的能力，提升数学素养。

[关键词]图形认知；几何直观；数学素养

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）02-0085-01

培养学生利用图形描述和分析数学问题的能力是课程标准提出的目标之一。教师应加强学生对图形的认知训练，帮助学生理解概念、算理、法则等，培养学生解决问题的能力。

一、加强图形认知，突破概念难点

很多学生能把一些概念背得滚瓜烂熟，但一到实际应用时就束手无策，原因是学生对概念的本质并没有很好地理解。教师应加强图形认知，将抽象的概念、定理与几何直观结合起来，化抽象为具体，化复杂为简单，带领学生轻松突破概念学习难点。

例如，教學“乘法分配律”时，课本中的图示如图1所示。笔者先出示图2，帮助学生建立概念与实物之间的联系。对于“一共贴了多少块瓷砖”，学生根据图示很快得出了两种计算方法：4×9+6×9和（4+6）×9。

笔者隐去图中的格子，得到直观的长方形图（如图3），然后追问：“已知长方形的长是10，宽是9，面积是10×9。10×9除了写成4×9+6×9=（4+6）×9的形式外，还有其他形式吗？”学生写出10×9=1×9+9×9，10×9=2×9+8×9，10×9=10×2+10×7，10×9=10×3+10×6等式子。通过对直观图的分拆，学生初步认识了乘法分配律的基本概念。最后，笔者出示图4，将具体的数字换成字母。学生通过分析、讨论、验证，得出了“（a+b）×c=a×c+b×c”的数学模型。

教师借助有序的图形认知，在实物直观、图形直观与乘法分配律之间建立有效的联系，让学生通过直观的长方形图，顺利突破了乘法分配律的难点。

二、加强图形认知，优化思维表达

逻辑表达往往过于抽象，但是数学直观恰恰能弥补这个不足，将复杂的文字变得更简单、更好理解。

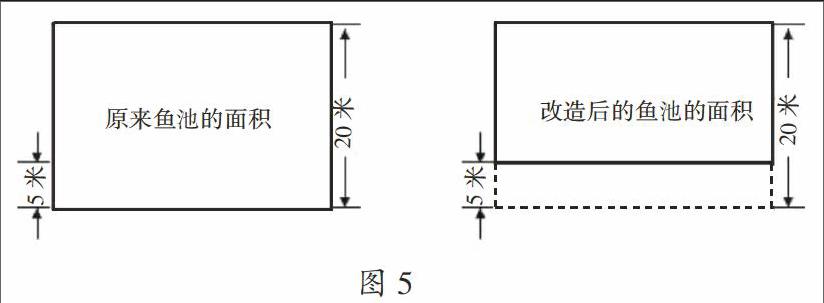
例如，教学“解决问题的策略”时，有这样一道习题：有一个宽20米的长方形鱼塘，改造后宽减少了5米，面积减少了150平方米，求改造后的鱼塘的面积。大部分学生先求出长方形的长，即 150÷5=30（米），进而得出改造后的鱼塘面积为30×（20-5）=450（平方米）。笔者要求学生画出直观图（如图5），学生根据直观图发现还可以这样思考：改造后的鱼塘的长没有变化，宽是20-5=15（米），是5米的3倍，那么改造后的鱼塘的面积是减少部分面积的3倍，即150×3=450（平方米）。

教师借助图形，让学生超越了长方形面积计算公式的逻辑转换，通过几何直观直接洞察问题的本质，优化了思维方式。

三、加强图形认知，引领数学建模

几何直观能有效表示出抽象的数学对象，培养学生的直观领悟能力。教师应加强学生对图形的认知，引领学生寻找数学对象的直观模型。

例如，教学“认识平均数”时，笔者出示男女生套圈的统计图，让学生观察并思考：“4名男生和5名女生分别组成两个代表队，哪一队套的平均圈数较多？”学生通过观察条形统计图，并进行移多补少的操作，很快得出结论。学生借助直观的条形统计图，认识到平均数的本质是“移多补少”，由此建立了直观的平均数数学模型。

教师利用条形统计图引领学生直观理解平均数的意义，形成了用“移多补少”的数学模型解决平均数问题的策略，培养了学生的逻辑推理能力。

总之，几何直观能力的培养是一个长期的过程，教师要引导学生学会利用图形寻找抽象概念与几何直观间的关联，突破知识难点，从而提升学生解决问题的能力。

（责编 韦 迪）endprint