基于层次分析法的大学生及格率因素探究

刘泽一，梁四化，宋辰雪，王 同，薛 冰

(长春师范大学数学学院，吉林长春 130032)

1 问卷调查

对于当代青年大学生来说，可谓是诱惑与机遇并存，而若在知识文化水平方面具备一定的优势便可以在一定程度上掌握机遇的先机。及格与否是衡量大学生知识文化水平的一个重要指标，目前国内外学者对于大学生进行学情分析。早在20世纪，美国研究了“全国大学生学习性投入调查”(NSSE)评价项目。我国清华大学于2007年结合中国国情与学生的实际情况，对中国大学生的学习情况进行深入研究[1]。然而专门对于影响大学生及格率因素的探索甚少，本文通过对东北地区某高校学生进行问卷调查，以期得到对大学生及格率影响因素探究的有益方向。通过回收有效问卷，对问卷结果进行系统整理分析，得到关于影响大学生及格率的19条因素，可分为个人、学校、家庭、社会四个方面。其中，个人层次包括年级、毕业方向、学习参与度、专业兴趣、学习能力、专业难度；学校层次包括学风建设、教师授课模式、资源共享程度、情感生活、学校学术氛围、奖励机制、人才培养方案；家庭层次包括家风建设、家庭经济水平、父母期望；社会层次包括社会就业压力、政府政策和社会舆论导向。

2 基于层次分析法影响大学生及格率因素评价体系构建

层次分析法(the analytic hierarchy process，AHP)，是20世纪70年代中期由美国运筹学家托马斯·塞蒂正式提出[2]。它是一种定性和定量相结合的、系统化、层次化的分析方法，是应用网络系统理论和多目标综合评价方法提出的一种层次权重决策分析方法。由于层次分析法在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。简而言之，就是将与决策有关的元素分为目标层、准则层及方案层，后在此基础上进行定性分析和定量分析，从中选出最优解，做出决策。

2.1 建立层次结构模型

2.1.1 符号说明

A表示目标层；Bj表示准则层第j个指标的名称(j=1,2,3,4)；Ci表示子准则层第i个指标的名称(i=1,2,…,19)；W1表示准则层对目标层的排序向量(权向量)组成的矩阵；W2表示子准则层对准则层的排序向量(权向量)组成的矩阵；W3表示子准则层对目标层的排序向量(权向量)组成的矩阵；λmax表示判断矩阵最大特征根；CI表示一次性指标；RI表示随机一次性指标；CR表示随机一次性比率。

[指导教师]梁四化(1980- )，男，副教授，硕士生导师，从事非线性微分方程研究。

2.1.2 层次构建

影响大学生及格率的因素评价体系包含目标层、准则层、子准则层(表1)。

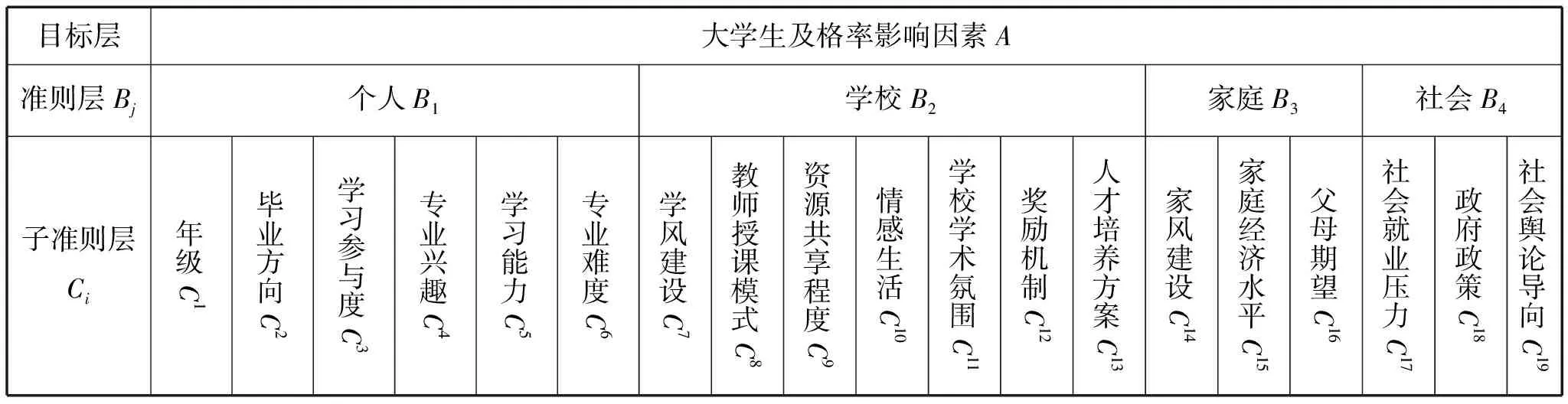
表1 影响大学生及格率因素层次表

大学生及格率影响因素作为总的评价目标，为目标层；主准则层由个人、学校、家庭、社会四个方面构成；子准则层为直接影响大学生及格率的具体指标。

2.2 构造影响大学生及格率因素评价判断(成对比较)矩阵

层次分析法的一大特点就是将主观判断量化，从而将定性分析转为定量分析。下面我们将所有因素两两比较，采用相对尺度来尽量减少各项因素的比较难度，提高准确度，构成判断矩阵并计算层次单排序权重值。判断矩阵是一层所有因素与上一层某一因素的相对重要性比较，判断矩阵的元素用aij表示(表2)。

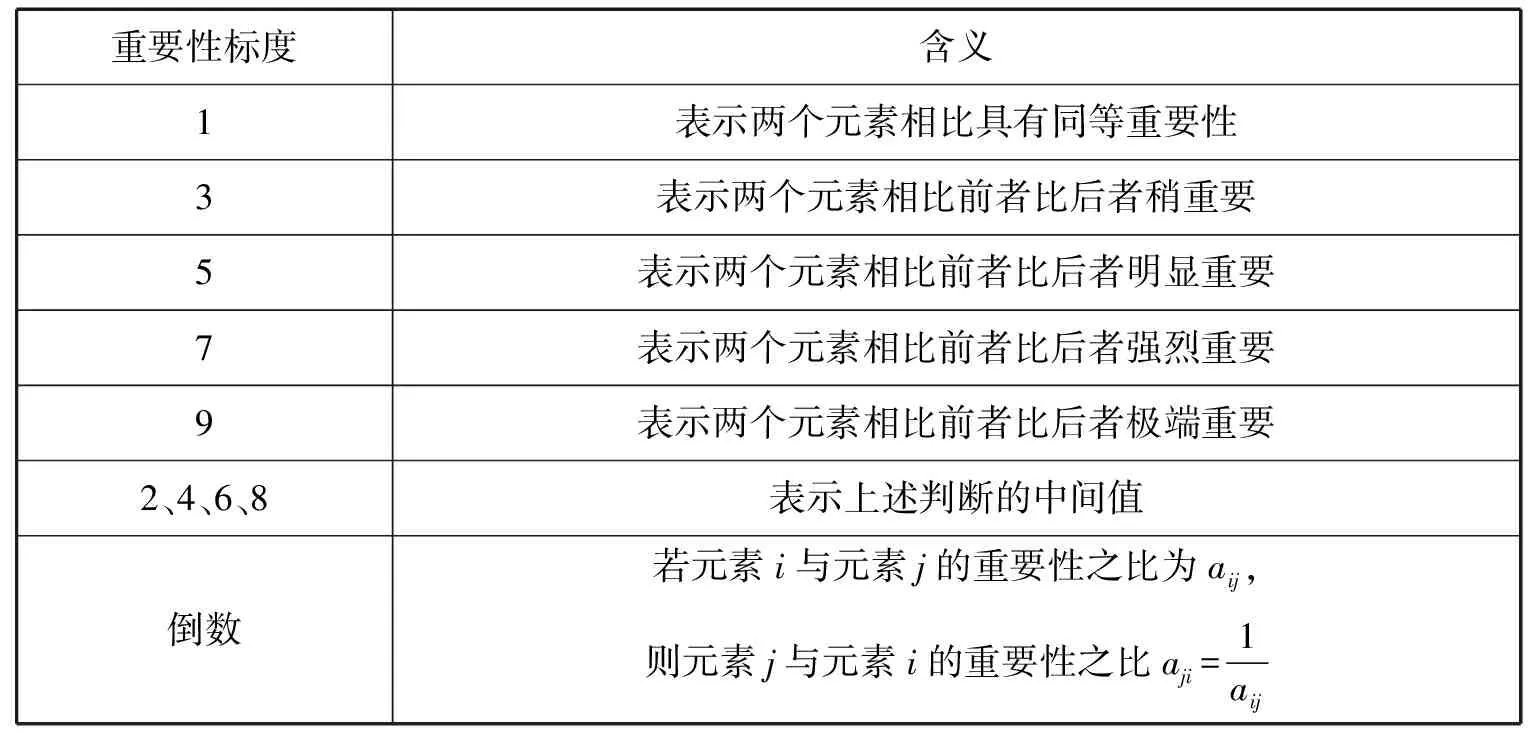
表2 重要性标度表

2.3 判断矩阵一致性检验及层次单排序

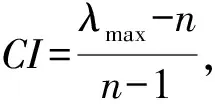
表3 平均随机一致性指标RI表

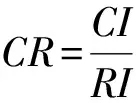
对所有判断矩阵进行层次单排序，即计算同一层次因素对上一层次因素的相对重要性权值，在此之前需要先进行一致性检验。层次单排序结果如表4至表8所示。

表4 判断矩阵A-Bj

表5 判断矩阵B1-Ci

表6 判断矩阵B2-Ci

表7 判断矩阵B3-Ci

表8 判断矩阵B4-Ci

2.4 层次总排序及其一致性检验

计算各层次全部因素对于目标层的合成权重，进行层次总排序。在进行层次总排序之前也需先进行一致性检验。经检验CR值小于0.1，满足一致性检验。合成权重结果如表9所示。

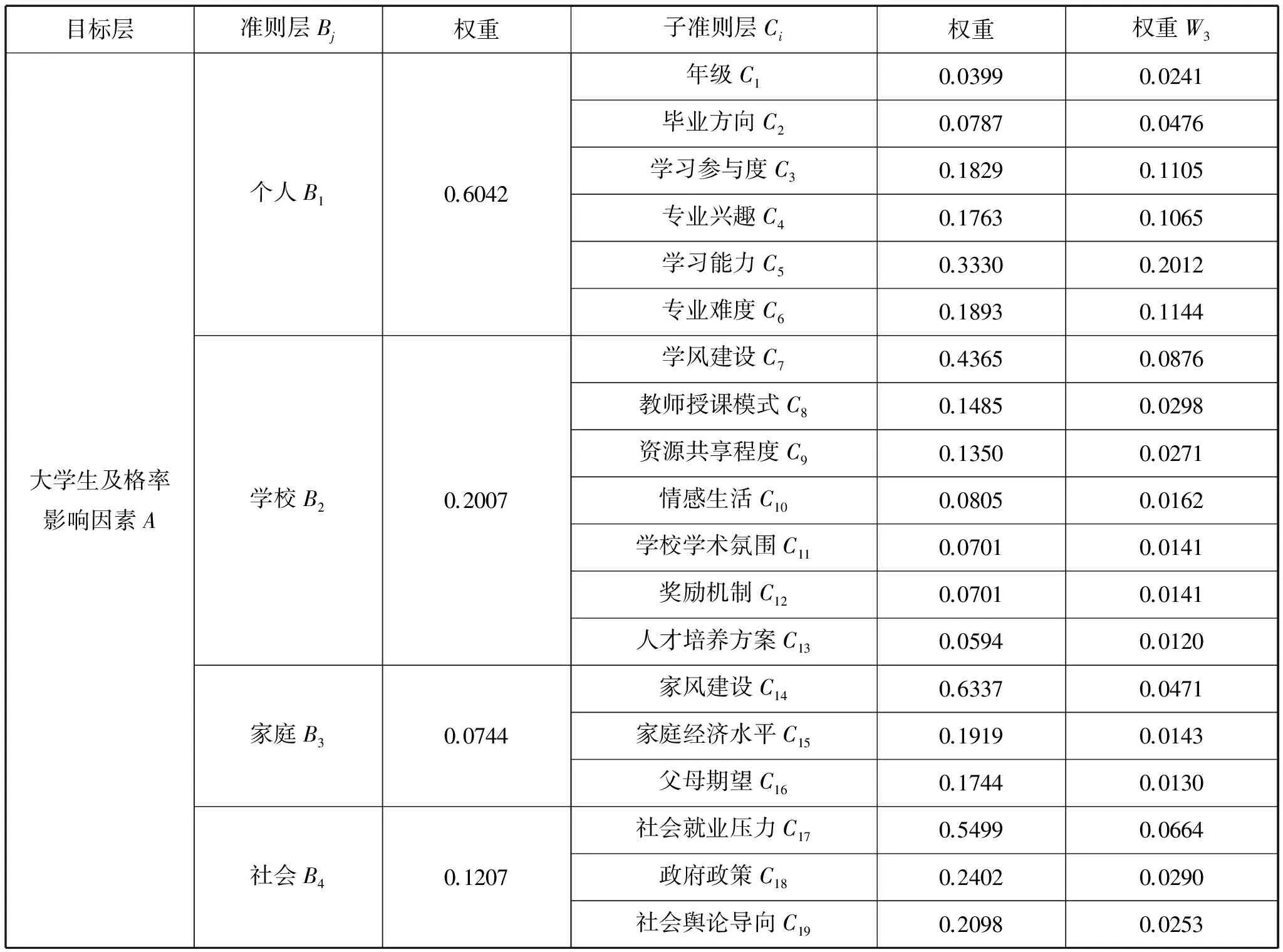
表9 合成权重结果

经层次总排序后发现，在个人层次中学习能力的权重值最高；学校层次中学风建设的权重值最高；家庭层次中家风建设的权重值最高；社会层次中社会就业压力的权重值最高。

3 建议

目前，中国高等教育已经进入大众化阶段，高等教育已经成为“现代社会的教育基础”。然而，教育系统日渐发展，国家投入力度不断加大，却仍然存在很大的“学习危机”，例如大学生学习自身动力不足，意志不够坚定，及格率较低，学校的教育模式和教师的授课方式不适应学生的需求，资源配置不均衡等。本文采用层次分析法建立模型，分析了大学生影响及格率的诸多因素，给出了较为合理的建议。从学生、教师、学校、家庭等层次入手，使结论及建议较为明确。

根据调查结果，调查小组针对占比重较大的因素提出如下建议：要想提高学生的学习能力，就要从提高内化和应用知识的能力、分析和整理信息的能力、追问和反思经验的能力这三个维度入手，指导学生学会建立自己的知识体系，达到知行合一。

[1]黄美娟.美国“全国大学生学习投入性调查”(NESS)研究[D].上海:上海师范大学,2014.

[2]周维超,童建刚,张海平.层次分析法在确立TBM围岩分级各地质因素权值中的应用[J].四川地质学报,2011(1):64-66.

[3]王连华,王松华.高校服务经济社会的数理评价指标体系研究——以上海为例[J].生产力研究,2011(8):107-108.

[4]代逸生,刘媛.基于MCCAA的工期成本质量的多目标优化分析[J].科学技术与工程,2012(19):4676-4680.

[5]徐跃.宁凯机加工分厂车间布局方案评价研究[D].南京:南京理工大学,2010.