数学建模思想在数学课程教学中的渗透

陈艳凌

(齐齐哈尔高等师范专科学校，黑龙江齐齐哈尔 161005)

数学模型是为了某种目的，用字母、数字及其它数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式。数学概念、数学理论体系、数学公式、方程式和算法都可称为数学模型[1]。

数学建模是根据具体问题，在一定假设下化简问题，建立起适合该问题的数学模型，求出模型的解，并对它进行检验，然后分析并检验所得到的解，以此确定建立的数学模型是否用于解决实际问题的多次迭代，不断深化的过程。

1 在数学课程中渗透数学建模思想的必要性

大学数学课程是高等院校各专业学生必学的基础课程。传统的课程主要讲解概念、定理、公式以及推论，教学重点放在数学的抽象性、严密性和逻辑性上，往往令学生感到乏味枯燥。正如李大潜院士所说：“过去的数学教学暴露出根本的缺陷，过于追求体系的天衣无缝，过于追求理论的完美和逻辑的严谨，忘记了数学从何处来又向何处去这个大问题，把数学建构成一个自我封闭的王国”[2]。数学建模正是联系数学理论知识与实际应用问题的桥梁，“将数学建模思想融入数学类主干课程”[3]，是数学课程教学改革的发展趋势。

1.1 调动学生学习积极性，激发学生参与探究的兴趣

兴趣是最好的老师。在大学数学中渗透数学建模思想，让学生在学习概念定理的基础上，运用知识解决实际问题，不仅能达到学以致用的效果，又能让学生加深对理论知识的理解，充分体会到数学本身就是刻画现实世界的数学模型，感受到数学的无处不在[4]。促使学生在实践中产生浓厚的探索兴趣，激发学习的热情。

1.2 增强理论联系实际的意识，提升大学生综合能力

部分大学生认为大学数学理论性过强，与实际生活相差甚远。在大学数学课程教学中渗透数学建模思想，可以提高学生学习数学知识的应用意识，培养学生用数学的思维方式。数学建模往往是由小组合作完成的，有利于培养学生的团队合作精神，提高学生的综合能力。

2 数学建模思想在数学课程教学中渗透的策略

2.1 建模思想在数学分析教学中的渗透

数学分析的主要教学内容是定义、概念、定理及推论，是从客观事物的某种数量关系或空间形式中抽象出来的数学模型。在教学中，应结合讲授内容，选取合适的案例，渗透数学建模思想。

例1 卖报人的卖报策略问题，卖报人每天早晨从报社购进日报进行零售，晚上把卖剩下的退给报社。

问题提出：请建立卖报人通过对每天购进报纸数进行控制来实现最大利润的数学模型。

假设：卖报人通过自己的经验和统计掌握了自己所负责的销售区域日需求量的随机规律，每天报纸的需求量为x份的概率是f(x)，(x=0，1，2，…)。假设每份报纸的零售价为m1元，购价为m2元，退回价为m3元，m1>m2>m3。假设每天卖报人购进了n份报纸，而需求量是随机的。当x≤n时，赚到(m1-m2)x元，赔了(m2-m3)(n-x)元；当x>n时，赚到(m1-m2)n元。卖报人每天购进n份报纸时,平均利润为I(n)元。得如下数学模型：

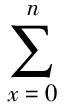
当需求量x的取值和购进量n都很大时，将x看作连续变量，f(x)转化为概率密度函数p(x)，则

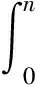
为求I(n)的最大值，要求I(n)对n的平均变化率。

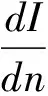
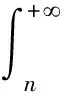
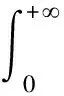
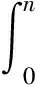
在定积分知识应用的教学中，通过解决卖报具体问题渗透数学建模思想，既巩固了定积分的知识结构，又提高了教学的趣味性，学生不再感觉概念定理枯燥，而是对抽象的知识有了亲近感，并获得成就感。通过模型假设—模型构成—模型求解—模型验证的一系列解题过程，培养了学生的探索意识，提高了学生实践能力。

2.2 建模思想在高等代数教学中的渗透

高等代数是大学数学各专业的基础课程，是数学在其它学科应用的必修课程，也是全国数学类硕士研究生入学考试必考课程。它具有严密的逻辑、系统的推理、抽象的思维，成为学生学习困难的数学课程。为了改变这种情况，可以尝试在高等代数教学中渗透数学建模思想。

2.2.1 在矩阵乘法中渗透风险型决策问题

矩阵乘法不同于任何数的乘法，其独特的算法往往让初学者感到理不清头绪。结合风险型决策问题，可以引发学生探索的欲望，使他们在解决问题过程中掌握矩阵乘法的算法。

例2 某企业要对某个问题进行决策(方案、自然状态、状态出现的可能性、收益值如表1所示)。试确定最优方案[5]。

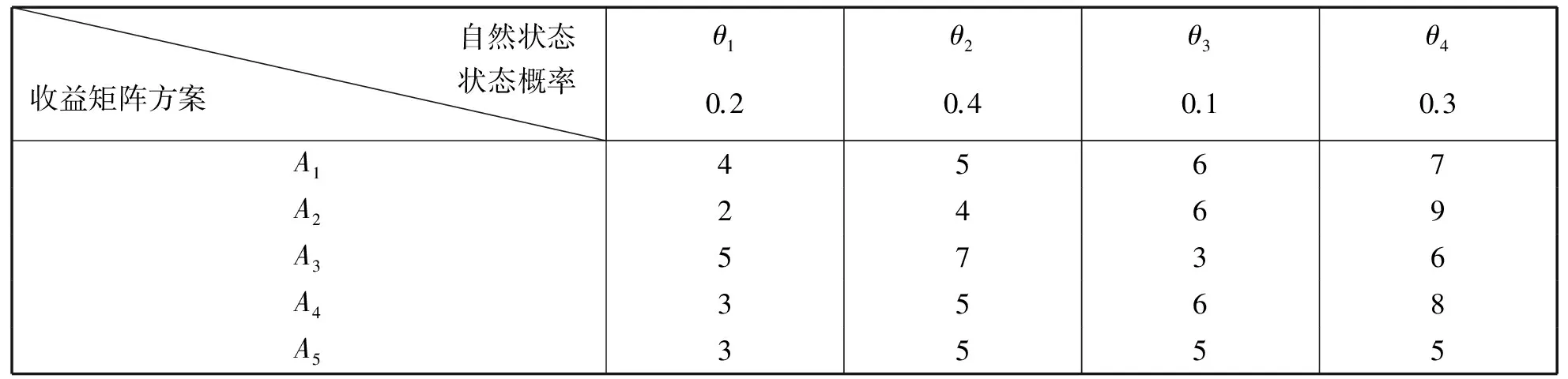
表1 某企业收益值表

Q中的最大值为5.9，对应的行动方案是A3，所以合理的决策是A3。

运用矩阵方法进行风险型决策，可以简化比较复杂、计算量比较大的决策问题的计算求解过程，又可将理论与实际联系起来，让学生感受矩阵乘法的重要性，产生探究的欲望。

2.2.2 线性方程组求解中渗透洗衣机品牌问题

例3 一项投资分析试图找出一家无商标洗衣机厂商的经营额。已知这家公司制造3种品牌的洗衣机，即品牌A,B,C。分析学家还知道该公司向供应商订了450000块1型电路板、300000块2型电路板及350000块3型电路板。品牌A用2块1型电路板、1块2型电路板及2块3型电路板；品牌B用3块1型电路板、2块2型电路板及1块3型电路板；品牌C用每种类型电路板各1块。

分析：分析学家只要计算出该公司制造的各种品牌的洗衣机的台数，就可知道该公司的营业额。

假设：该公司制造的三种品牌的洗衣机分别为x1,x2,x3台，则可列出线性方程组：

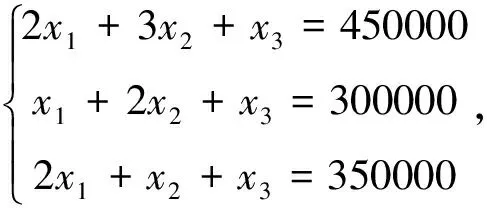
容易计算出系数矩阵与增广矩阵有相等的秩，所以方程组有唯一的解，即能求出该公司制造的3种品牌的洗衣机的台数。

通过模型假设—模型构成—模型求解—模型验证的一系列解题过程，不仅巩固了线性方程组求解，而且培养了学生的探索意识，提高了学生实践能力。

3 结语

把数学建模思想渗透到数学课程教学中，有利于学生学习大学数学抽象的概念、定理及推论，激发学生的学习兴趣，培养学生的探究意识和实践能力。但是这种结合还在不断探索中，随着大学数学教育教学改革的不断发展，仍需要广大高等学校数学教师及数学爱好者继续探索研究。

[1]顾泠沅,朱成杰.数学思想方法[M].北京:中央广播电视大学出版社,2004.

[2]曹燕.数学建模思想在高等数学课程教学中的渗透[J].科学大众(科学教育),2013(5):137,165.

[3]李大潜.将数学建模思想融入数学类主干课程[J].中国大学教育,2006(1):9-11.

[4]韦程东,罗雪晴,程艳琴.在数学分析教学中融入数学建模思想的探索与实践[J].高教论坛,2008(3):77-79.

[5]刘仲奎,杨永保,程辉,等.高等代数[M].北京:高等教育出版社,2003.