水的状态与体积、压力和温度间的关系

金成树，崔英资，于冬梅，孙红梅，侯 林，郎德龙

(绥化学院食品与制药工程学院，黑龙江绥化 152061)

水是地球上非常重要的物质，在生命的环境中起着重要作用。河流中水的循环，雨、雾、雪和霜等的形成都与水的状态有关，水在工农业生产中有着非常广泛的应用。因此，了解和研究水的状态、温度、压力和体积间的关系是非常必要的。

1 水的空间状态图

图1是在压力不太高时且不存在空气或惰性气体影响时水的空间状态图[1-4]。相律的方程式为f=k-P+Z，其中f表示体系的自由度数，k表示体系的独立组分数，P表示体系处于平衡状态时的相数，Z表示温度和压力等影响因素(一般情况下Z=2，即仅考虑温度和压力因素)。EYRME曲面表示普通固态水即冰Ⅰ的温度、体积和压力之间的关系，该曲面上点的自由度数为2。CND曲面表示液态水(即未饱和水)的温度、体积和压力之间的关系，该曲面上点的自由度数为2。C表示临界点(647.29K，22.09 MPa)，此时气液相无差别。CWHG曲面表示气态水(即过热水蒸气)的温度、体积和压力之间的关系，该曲面上点的自由度数都为2。注意，过热水蒸气是指在相同的压力下其温度高于饱和水蒸气所对应的温度的气态水。LMN表示等温等压的三相线，线上所有点的自由度数都为0。DNMED曲面表示冰Ⅰ和液态水的平衡共存面，CNMLWC曲面表示液态水和饱和水蒸气的平衡共存面，JLMRJ曲面表示冰Ⅰ和饱和水蒸气的平衡共存面，上述三个两相平衡共存面上点的自由度数为1。垂直于lgV轴的平面上的HWLJ线上所有点的体积都相同。垂直于lgp轴的平面上的GDEY曲线上所有点的压力都相同。液态水和气态水的分界线大致在临界点温度或稍低于该温度的附近。-99℃时冰Ⅰ的蒸气压为0.0016Pa[5]。-60℃和-120℃时固态水的密度分别为0.924g/cm3和0.929g/cm3[6]。可见，温度低于-99℃时水的蒸气压可被忽略掉，R点的温度低于-99℃。JR线上所有点的温度都相同。

本文中V都表示摩尔体积。图1中点、线和面以外的空间与水的状态没有任何联系。在本文所有图中，lgp和lgV都表示相应的压力p和摩尔体积V的对数值，p的单位是MPa，V的单位是m3/mol。当压力p和摩尔体积V等于零时，lgp和lgV都趋于负无穷大，这是该方法的缺点。如直接采用压力p和摩尔体积V为坐标，则会带来绘图困难或曲线形状不规则问题。

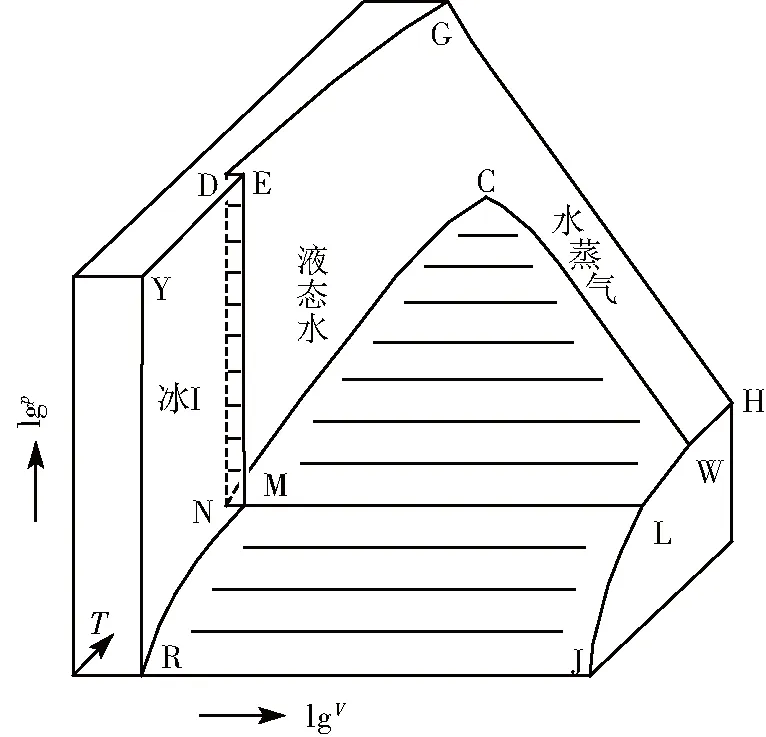
图1 在压力不太高时水的空间状态图

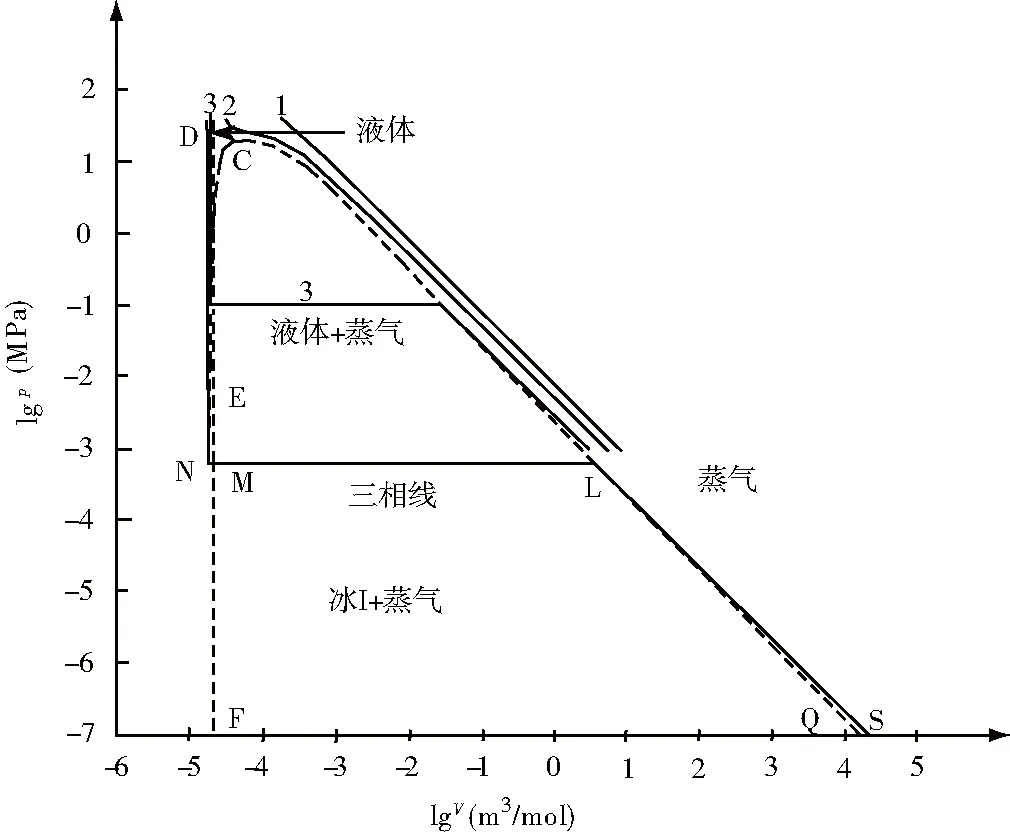
图2 在压力不太高时水的lgp-lgV状态图

2 水的lgp-lgV和lgp-T状态图

2.1 水的lgp-lgV图

图2是在压力不太高时水的空间状态图在lgp-lgV平面上的等温截线图。1号等温截线表示973.15K时的过热水蒸气[6]的等温截线，温度高于临界点温度，水蒸气不能液化。2号等温截线表示653.15K时的过热水蒸气[6]的等温截线，这时温度稍微高于水的临界点的温度。3号等温截线(实线)表示373.15K时的等温截线[6]，该等温截线分别穿过液相区、液气两相平衡共存区和气相区，等温等压的平台的自由度数为0(由于温度已知)，截线中非平台部分的点的自由度数为1。DNMLS等温截线(实线)的温度等于水的三相线(NML)的温度，该等温截线分别穿过液相区、固液气三相平衡共存区和气相区，等温等压的三相线平台中自由度数为0，截线中其余的非平台部分的点的自由度数为1，实线LS上的摩尔体积是用理想气体状态方程计算的(温度为273.16K)。虚线LQ上点的摩尔体积是根据冰Ⅰ在不同温度下的饱和蒸气压数据用理想气体状态方程计算的，它是冰Ⅰ的饱和蒸气压曲线在lgp-lgV平面上的投影线(不是等温截线)。虚线CM是液态水的摩尔体积曲线在lgp-lgV平面上的投影线。虚线CL是液态水的饱和蒸气压曲线在lgp-lgV平面上的投影线。气态水和液态水曲面在图2中lgp-lgV平面上的投影明显，而固态冰Ⅰ曲面(图1中EYRME曲面)在图2中lgp-lgV平面上的投影是非常狭窄的曲面(虚线EMF所占据的位置)。液态水在高压下具有可压缩性，如0℃时在500atm(50.6625MPa)下体积缩小到原来的0.9767倍[6]。

2.2 水的lgp-T图

在图3中，lgp-T状态图是水的空间状态图在lgp轴和T轴构成平面上的投影图，不是等容截线。临界点至三相点的实线CN是液态水和气态水的平衡共存线(图1中的CNMLWC曲面在lgp-T平面上的投影线)。实线NF是固态水和气态水的平衡共存线(图1中的JLMRJ曲面在lgp-T平面上的投影线)。实线BN是固态水和液态水的平衡共存线(图1中的DNMED曲面在lgp-T平面上的投影线)。在固态冰Ⅰ和液态水的平衡共存线中，普通固态冰Ⅰ的熔点分别为0.0025℃、-5.0℃、-10.0℃、-15.0℃和-20.0℃时，对应的压力分别为0.101325MPa、59.8MPa、110.4MPa、156.0MPa和193.5MPa[3])。而亚稳态的过冷液态水的饱和蒸气压(过冷液态水在-3℃、-6℃、-9℃、-12℃和-15℃时的蒸气压分别为489.7MPa、390.8MPa、310.1MPa、244.5MPa和191.5Pa[7])比相同温度时的冰Ⅰ的饱和蒸气压稍大一点(冰Ⅰ在-3℃、-6℃、-9℃、-12℃和-15℃时的蒸气压分别为475.614Pa、368.575Pa、284.062Pa、217.546Pa和165.425Pa[6])，AN线表示过冷液态水的饱和蒸气压曲线。

在压力不大时普通的冰称为冰Ⅰ，当压力达到214.2MPa左右，会出现其他类型的冰。N点(273.16K，0.6113KPa)的三相分别是冰Ⅰ、液态水、气态水。冰Ⅰ、冰Ⅲ、液态水的三相点的温度和压力分别为251.15K和214.2MPa。冰Ⅰ、冰Ⅱ、冰Ⅲ的三相点的温度和压力分别为238.45K和219.8MPa。冰Ⅱ、冰Ⅲ、冰Ⅴ的三相点的温度和压力分别为248.85K和355.6MPa。冰Ⅲ、冰Ⅴ、液态水的三相点的温度和压力分别为256.15K和357.6MPa。冰Ⅴ、冰Ⅵ、液态水的三相点的温度和压力分别为273.31K和646.3MPa。冰Ⅵ、冰Ⅶ、液态水的三相点的温度和压力分别为354.75K和2269.1MPa。图3中每个三相点的自由度数都为0，而每条线上点(除三相点外)的自由度数都为1。由上述可见，固态冰的熔点与压力有关，高压的影响不可忽略。

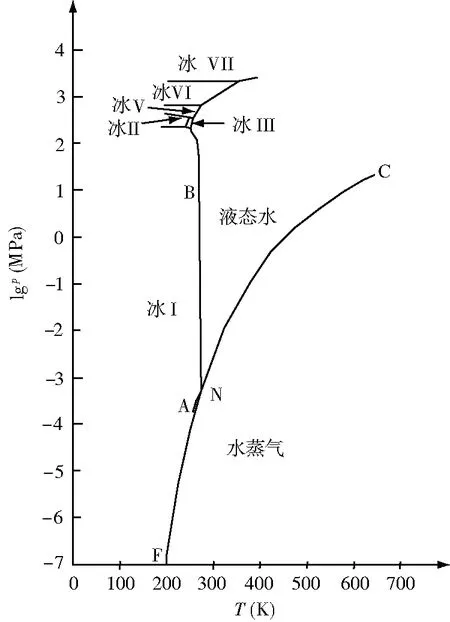
图3 水的lgp-T状态图

3 讨论和结论

水处于闭合体系中并且没有空气或惰性气体存在时，纯物质处于平衡状态的两相间压力与温度之间的关系符合Clapeyron方程，即

(1)

(2)

其中,R表示普适气体常数。图3中的每个两相平衡共存线都符合Clapeyron方程。

由惰性气体产生的外压对饱和蒸气压的数值是有影响的，假设实际气体为理想气体，它们之间的关系式为:

(3)

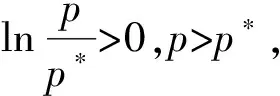
在一定温度下，稀溶液中溶剂的蒸气压等于纯溶剂的蒸气压乘以溶剂的摩尔分数，称为拉乌尔(Raoult)定律。因此，非挥发性溶质的加入可使溶剂的蒸气压降低，将导致水溶液的凝固点降低，沸点升高。如海水的凝固点比纯水低，自来水等因含杂质沸点比纯水高。

液体表面的形状会影响液体的饱和蒸气压，并符合Kelvin公式[8]，即

(4)

其中，(4)式推导时假设了实际气体为理想气体，p*表示液体表面为平面时的饱和蒸气压(该值会受惰性气体压力影响)，p表示小液滴的饱和蒸气压，γ表示液体的表面张力，M表示液体的摩尔质量，ρ表示液体的密度，r表示小液滴的半径。根据Kelvin公式可知，在相同的温度下，小液滴半径越小，饱和蒸气压越大(lnp/p*与r成反比)。但r在数量级上明显改变时，lnp/p*的值变化不大。

Kelvin公式可以帮助我们更好地理解雾的形成和消失的原因。在温度高时，大气中气态水在一般情况下的实际蒸气压p值小于小液滴的饱和蒸气压p值，不能形成雾。但在温度低时水蒸气的饱和蒸气压p*值会减少，实际蒸气压p值达到或大于小液滴的饱和蒸气压p值，大气层中的气态水将凝结为小液滴析出并漂浮在大气中而形成雾。在形成雾后，如果温度升高，则饱和蒸气压p*值也将在理论上不断增大，小液滴必须使自身的半径不断变小来增加小液滴的饱和蒸气压p值，甚至于使雾消散，否则(4)式左边理论上有变为零或负值的可能，将违背(4)式。实际蒸气压p值小于饱和蒸气压p*值时，小液滴只能消散为气体。当实际蒸气压p值远大于小液滴的饱和蒸气压p值，也会使(4)式两端数值不相等，这将导致气态水凝结为小液滴，直至小液滴半径不断增大形成雨或露水(而不是雾)并落到地面。当然在气温很低时，气态水将凝结为雪或霜。

雪和霜等是气态水在低温下凝结而成的小冰晶，它们的密度要小于普通固态冰Ⅰ。在升温至0℃时雪和霜能熔化为液态水(当然具体的熔化温度也会受到杂质和气压的影响)。在冬季或冰箱冰柜中，气态水会凝固为雪或霜(不是大块冰)。由于雪和霜中小冰晶间接触的紧密程度不如大块冰，故传热慢，在相同的条件下比大块冰熔化速度要慢。

[1]陈运生.物理化学分析[M].北京:高等教育出版社,1987.

[2]Borgnakke C,Sonntag R E. Fundamentals of Thermodynamics[M].Singapore: John Wiley & Sons Singapore Pte. Ltd.,2014.

[3]胡英.物理化学：上册[M].4版.北京:高等教育出版社,2005.

[4]金成树.簇合物的规则和热力学第二定律[M].哈尔滨:黑龙江科学技术出版社,2016.

[5]张向宇.实用化学手册[M].2版.北京:国防工业出版社,2011.

[6]刘光启,马连湘,刘杰.化学化工物性数据手册(无机卷) [M].北京:化学工业出版社工业装备与信息工程出版中心,2002.

[7]孙尔康,徐维清,邱金恒.物理化学实验[M].南京:南京大学出版社,1998.

[8]梁山,崔玉红,郭艳玲.外压与凝聚态物质饱和蒸气压关系的讨论[J].大学化学,2013(4):67-69.