基于数学建模的连体数独的求解问题研究
2018-03-05柯春梅
柯春梅
(厦门海洋职业技术学院基础部,福建厦门 361101)
数独就是在一个包含一定单元格的区域内,根据题目类型给定的规则,通过已知数字推理出剩余未知数字的一类数字谜题.数独按照条件、规则,可分为标准数独和变形数独.连体数独是一款变形数独,它是指两个或者多个具有若干共同格子的数独连成一体,构成的另外一种数独,其解题规则是:在不相交部分,求解要求与单个数独的要求完全一样,在相交部分,其数字既是第一个数独的,也是第二个数独的[1].连体数独不是由可以单独解开的数独合并到一起的,合格的连体数独是以整体出现时可以求解,而拆分开来是无法单独求解的.连体数独连的方式多种多样,常见的有二连体数独、三连体数独、四连体数独(僧侣数独)、五连体数(武士数独、花型数独、异形五连体数独)、六连体数独、九连体数独、十一连体数独等[2-3].数独问题可以看作优化问题,通过建立数学模型,并利用LINGO软件进行求解,目前这种研究不多,胡英武[4]给出九阶数独的模型与求解程序,马丽娜[5]给出对角线数独的模型与求解程序,柯春梅[6-7]给出了标准数独、对角线数独、窗口数独、额外区域数独、奇偶数独及杀手数独的求解程序,对于连体数独的建模与求解问题,目前尚未看到相关研究.这里基于数学建模研究五连体数独的求解问题,这些思路与方法可以推广到其他连体数独的求解问题.
1 提出问题
图1所示的五连体数独称为武士数独,是由五个数独组成的,其中中间数独和其他四个数独都有一个共同的小九宫.我们按照符号假设、模型建立与模型求解等数学建模基本步骤来建立武士数独的数学模型,编制相应的LINGO程序,并以图1为例求解.然后将模型推广,建立花型数独的数学模型,编制相应的LINGO程序,并举例求解.
2 符号假设
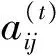
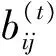

图1 武士数独
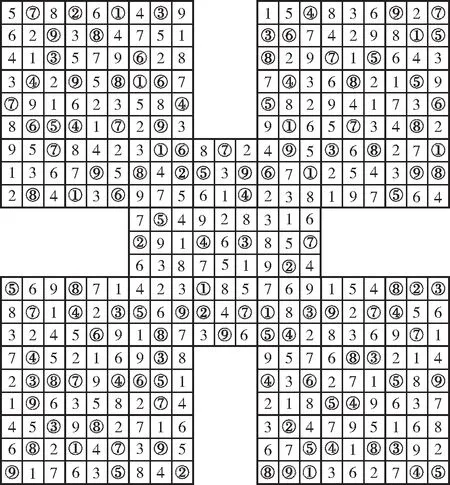
图2 武士数独的解
Bmt={(i,j)|3int[(i-1)/3]+int[(j-1)/3]+1=mt},t=1,2,3,4,5;Bmt表示第t个数独的第m个小九宫.
3 建立模型
连体数独的求解问题可以转化为数学规划问题,数学规划问题的三要素是决策变量、目标函数和约束条件.
决策变量:由于格子(i,j)处要么填入数字k,要么不填入数字k(k=1,2,…,9),有且只有两种状态,因而引入三元0-1变量:
目标函数:由于数独的可行解是唯一的,连体数独的可行解也是唯一的,该可行解就是目标函数,所以连体数独的目标函数为min=1.
约束条件:根据数独的填数规则和连体数独的概念,武士数独的约束条件为:
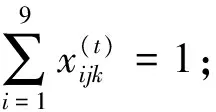
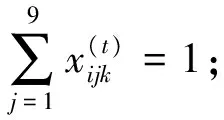
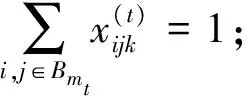
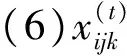
(7)公共部分的数字满足相交的两个数独的条件:
根据上述分析可知,武士数独的数学模型为:
4 模型的求解
LINGO是求解优化问题的专业软件包,它内置建模语言,提供几十个内部函数,从而能以较少的语句,较直观的方式描述大规模的优化模型,而且它的运算速度快,计算结果可靠[8].利用LINGO编程语言,对上述模型编制程序如下:
model:
sets:
number/1..9/;
line/1..9/;
col/1..9/;
gong/1..9/;
shudu(line,col):b1,b2,b3,b4,b5,a1,a2,a3,a4,a5;
link(line,col,number):x1,x2,x3,x4,x5;
endsets
data:
!键盘输入;
a1=?;
a2=?;
a3=?;
a4=?;
a5=?;
enddata
@for(line(i):@for(col(j):b1(i,j)=@sum(number(k):k*x1(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x1(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x1(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x1(i,j,k))=1));

@for(link(i,j,k):@bin(x1(i,j,k)));
@for(line(i):@for(col(j):b2(i,j)=@sum(number(k):k*x2(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x2(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x2(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x2(i,j,k))=1));

@for(link(i,j,k):@bin(x2(i,j,k)));
@for(line(i):@for(col(j):b3(i,j)=@sum(number(k):k*x3(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x3(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x3(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x3(i,j,k))=1));

@for(link(i,j,k):@bin(x3(i,j,k)));
@for(line(i):@for(col(j):b4(i,j)=@sum(number(k):k*x4(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x4(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x4(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x4(i,j,k))=1));

@for(link(i,j,k):@bin(x4(i,j,k)));
@for(line(i):@for(col(j):b5(i,j)=@sum(number(k):k*x5(i,j,k))));
@for(line(i):@for(col(j):@sum(number(k):x5(i,j,k))=1));
@for(line(i):@for(number(k):@sum(col(j):x5(i,j,k))=1));
@for(col(j):@for(number(k):@sum(line(i):x5(i,j,k))=1));

@for(link(i,j,k):@bin(x5(i,j,k)));
End
键盘输入
a1=0 1 6 0 7 0 0 9 0
8 0 2 5 0 9 6 0 1
0 0 0 0 0 4 0 0 0
0 5 0 0 0 0 0 0 0
2 0 0 4 0 3 0 0 7
0 0 0 0 0 0 0 2 0
0 0 0 1 0 0 0 0 0
5 0 9 2 0 7 1 0 3
0 8 0 0 9 0 5 4 0; a2=0 7 0 2 0 1 0 3 0
0 0 9 0 8 0 0 0 0
0 0 3 0 0 0 6 0 0
0 4 0 9 0 8 1 6 0
7 0 0 0 0 0 0 0 4
0 6 5 4 0 7 0 9 0
0 0 7 0 0 0 0 1 6
0 0 0 0 9 0 8 0 2
0 8 0 1 0 6 0 0 0; a3=0 0 4 0 0 0 9 0 7
3 6 0 0 0 0 0 1 5
8 0 0 7 0 5 0 0 0
0 4 0 0 8 0 0 5 0
5 0 0 0 0 0 0 0 6
0 1 0 0 7 0 0 8 0
0 9 0 3 0 8 0 0 1
6 0 1 0 0 0 0 9 8
0 0 0 0 0 0 5 0 0;
a4=5 0 0 8 0 0 0 0 0
0 7 0 4 0 3 5 0 9
0 0 0 0 6 0 0 8 0
0 4 0 0 0 0 0 3 0
0 3 8 7 0 4 6 5 0
0 9 0 0 0 0 0 7 0
0 0 3 0 8 0 0 0 0
0 8 0 1 0 7 0 9 0
9 0 0 0 0 5 0 0 2; a5=0 0 0 0 0 0 8 2 3
1 0 3 9 0 7 4 0 0
5 4 0 0 0 0 0 7 0
0 0 0 0 8 3 0 0 0
4 0 6 0 0 0 5 0 9
0 0 0 5 4 0 0 0 0
0 2 0 0 0 0 0 0 0
0 0 5 4 0 8 3 0 0
8 9 1 0 0 0 0 4 5;
运算后可得到武士数独的解如图2所示.
5 模型检验
武士数独的数学模型和求解程序具有普遍适用性.对于不同的武士数独,我们只要输入相应的数据a1,a2,a3,a4,a5就可以得到它的解.利用百度搜索可以搜到很多武士数独,这里选取文献[9]中10个武士数独进行验证,可以得出正确的解,而且求解速度在1秒以内.
6 模型的推广
图3所示的五连体数独称为花型数独[3],它是由图5所示的5个数独组成,从左到右的数独分别是第1数独、第2数独、第3数独、第4数独、第5数独.
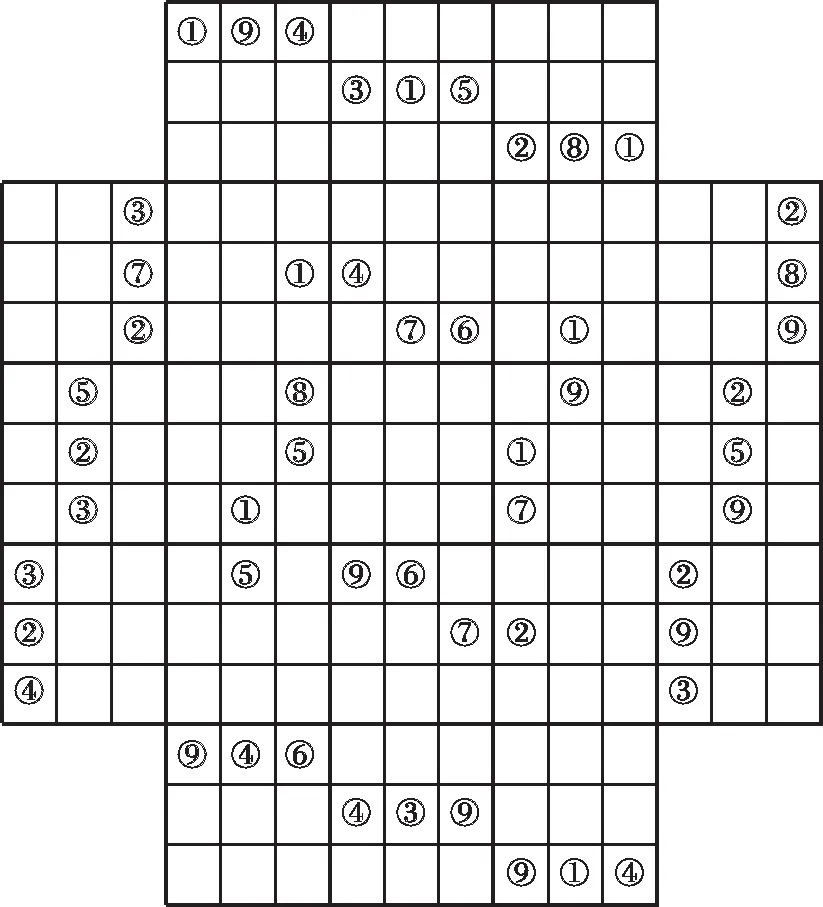
图3 花型数独

图4 花型数独的解

图5 组成花型数独的5个数独
按照前面的符号假设,将武士数独模型的最后4行修改为:
相应地,将武士数独求解程序的最后4行修改为:
键盘输入
a1=1 9 4 0 0 0 0 0 0
0 0 0 3 1 5 0 0 0
0 0 0 0 0 0 2 8 1
0 0 0 0 0 0 0 0 0
0 0 1 4 0 0 0 0 0
0 0 0 0 7 6 0 1 0
0 0 8 0 0 0 0 9 0
0 0 5 0 0 0 1 0 0
0 1 0 0 0 0 7 0 0; a2=0 0 3 0 0 0 0 0 0
0 0 7 0 0 1 4 0 0
0 0 2 0 0 0 0 7 6
0 5 0 0 0 8 0 0 0
0 2 0 0 0 5 0 0 0
0 3 0 0 1 0 0 0 0
3 0 0 0 5 0 9 6 0
2 0 0 0 0 0 0 0 7
4 0 0 0 0 0 0 0 0; a3=0 0 0 0 0 0 0 0 0
0 0 1 4 0 0 0 0 0
0 0 0 0 7 6 0 1 0
0 0 8 0 0 0 0 9 0
0 0 5 0 0 0 1 0 0
0 1 0 0 0 0 7 0 0
0 5 0 9 6 0 0 0 0
0 0 0 0 0 7 2 0 0
0 0 0 0 0 0 0 0 0;
a4=0 0 0 0 0 0 0 0 2
4 0 0 0 0 0 0 0 8
0 7 6 0 1 0 0 0 9
0 0 0 0 9 0 0 2 0
0 0 0 1 0 0 0 5 0
0 0 0 7 0 0 0 9 0
9 6 0 0 0 0 2 0 0
0 0 7 2 0 0 9 0 0
0 0 0 0 0 0 3 0 0; a5=0 0 8 0 0 0 0 9 0
0 0 5 0 0 0 1 0 0
0 1 0 0 0 0 7 0 0
0 5 0 9 6 0 0 0 0
0 0 0 0 0 7 2 0 0
0 0 0 0 0 0 0 0 0
9 4 6 0 0 0 0 0 0
0 0 0 4 3 9 0 0 0
0 0 0 0 0 0 9 1 4;
运行后可得到该花型数独的解如图4所示.用文献[3]中的练习题进行验证,同样可以在1秒内得到正确答案.
构成连体数独的单个数独可以是九阶的,也可以是非九阶的,还可以是变形数独.连体数独,可以两个数独有共同格子的连体,也可以是多个数独有共同格子的连体,而且连体的方法多种多样,但它们的解题规则是一样的.上述建模和求解的思路与方法可以推广到各种连体数独的情形.
7 结语
数独是一款益智数字游戏,它全面考验做题者的观察能力和推理能力,虽然玩法简单,但数字排列方式却千变万化,是训练头脑的绝佳方式,引起许多民众特别是青年学生的兴趣,每年的中国数独锦标赛都吸引众多学生的参加.数独的求解问题可以转化为数学规划问题,先建立数学模型,建模过程包括符号假设、模型建立、模型求解、模型推广等,再用LINGO软件编程求解.用数学建模的方法求解连体数独具有可推广性,数学模型和求解程序简洁,运算时间短,结果准确.将基于数学建模的数独求解问题用于数学建模的培训,能引起学生的兴趣,可以训练建模的基本步骤,还能训练LINGO软件的应用,对提高培训效果起到积极的作用.
[1]严德人.竞技数独[M].北京:中国言实出版社,2007.
[2]余俊雄,尤国峻.数独揭秘[M].武汉:湖北少年儿童出版社,2011.
[3]芦向明,蓝天.非常数独:一本书玩够76种花式数独[M].北京:化学工业出版社,2011.
[4]胡英武.数独问题的整数规划模型[J].金华职业技术学院学报,2011(6):86-88.
[5]马丽娜.对角线数独的LINGO求解模型[J].电脑知识与技术,2015(4):91-93.
[6]柯春梅.数独的数学模型与LINGO求解程序[J].长春师范大学学报,2016(12):8-13.
[7]柯春梅.杀手数独的数学模型与LINGO求解程序[J].呼伦贝尔学院学报:汉文版,2016(6):85-88,91.
[8]袁新生,邵大宏,郁时烁.LINGO和Excel在数学建模中的应用[M].北京:科学出版社,2007.
[9]百度贴吧.一组武士数独(数独吧)[EB/OL].(2015-11-12)[2017-05-29].http://tieba.baidu.com/p/4173732197.
