GCL13型鼓形齿联轴器的结构参数分析与优化
2018-03-05杜克飞
杜克飞
(马鞍山钢铁股份公司,安徽马鞍山 243000)
0 引言
鼓型齿联轴器作为机械传动的重要运动构件,由于其结构的复杂性,为此很多学者对它的力学性能进行了研究,而本文在前人研究结果[1-4]的基础上,利用ANSYS有限元分析软件对鼓型齿联轴器的全齿对接触模型进行了静力学分析,在轴线对中的情况下,利用了有限元方法系统地研究了齿位移圆半径和压力角主要参数对GCL13型鼓形齿联轴器的力学性能和承载性能的影响。为GCL13型鼓形齿联轴器的参数优化提供了理论依据。
1 GCL13型鼓形齿联轴器参数
GCL13型鼓形齿联轴器是由内齿圈、外齿轴套和螺栓组成的。其装配如图1所示。
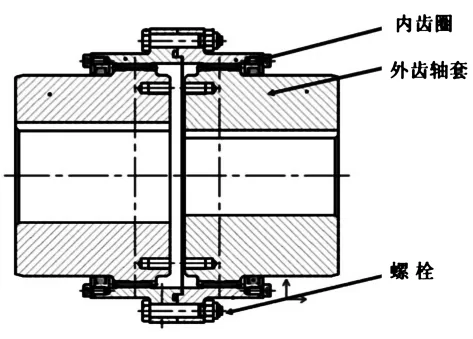
图1 鼓形齿联轴器的装配图
主要技术参数为:齿数z=80;模数m=2 mm;齿形角α=20°;齿顶高系数=0.8;鼓度系数ε=r/R=160÷265=0.604;公称转矩T=63 kN·m;许用转速n=1850 r/min;两周偏转角ωmax=1.5°;螺栓拧紧力矩MA=149 N·m。
2 有限元模型的建立
2.1 鼓形齿模型的简化
齿轮啮合实际是轮齿齿面之间相互接触作用,它是一种高度非线性行为,为了节省计算资源,应对鼓形齿联轴器的整体模型进行简化,由于只需要了解齿轮两接触面之间的受力情况,所以建立内齿圈和外齿轴套的有限元模型既可。但是如果采用单个齿的有限元模型,则计算结果与建立全部齿轮的计算结果相差较大。综合考虑采用建立全齿模型,如图2所示。
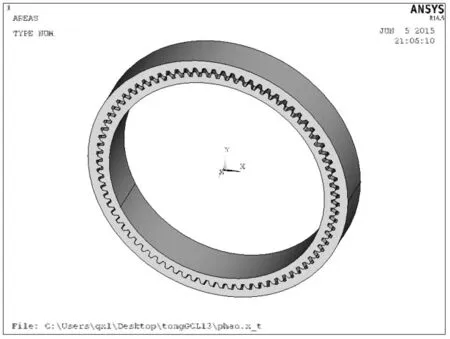
图2 装配体简化模型
2.2 离散模型的建立
为了保证计算精度,本文采用8节点的4面体单元solid185对鼓形齿联轴器划分网格,模型全部采用扫略方法划分得到六面体网格[5-6],且对关键部位(接触的齿)进行网格细化程序处理,离散模型如图3所示;联轴器材料为42CrMo,屈服极限为930 MPa,设置其弹性模量为2.06×1011Pa,泊松比为μ为0.3。
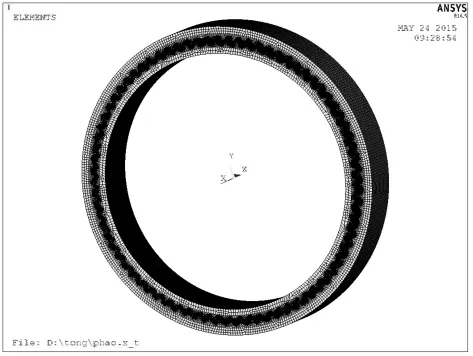
图3 划分网络后的鼓形齿
2.3 载荷与约束
根据GCL13型鼓形齿联轴器的实际工作情况,先对鼓形齿联轴器的内齿圈的外表面施加约束;然后再在柱坐标系下,对外齿轴套的内孔表面施加径向约束,并且在其两外端面施加轴向约束。
对外齿轴套的内孔表面上的节点,施加的切向力F为

式中:F为节点受到的切向力的大小,N;T为公称转矩,N·m;R为外齿轴套的内孔半径,m;N为外齿轴套的内孔表面节点个数。
将GCL13型鼓形齿联轴器的相关参数代入公式(1),查得节点数为18 544通过计算可以得到外齿轴套的内孔表面施加的切向力F=23.429 N。GCL13型鼓形齿联轴器的加载约束后的图如图4所示。
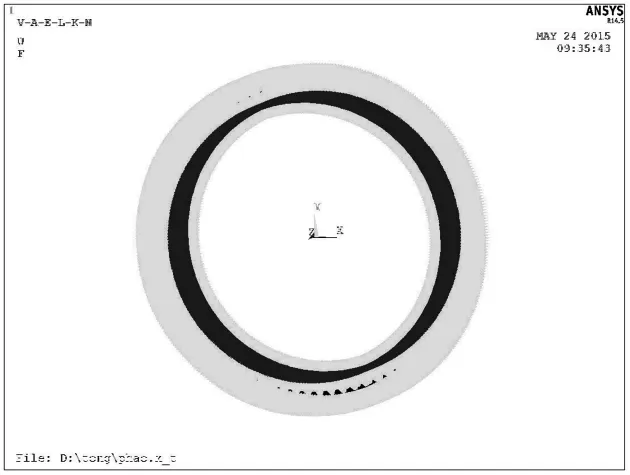
图4 施加载荷和约束
2.4 求解及静力学仿真
为了使求解过程快速而又收敛,而又减少有限元分析的运算时间,并获得更加精确的结果,分析中设置一个载荷步的加载方式,将这一载荷步又分为50个子步,每个子步又将该载荷分成很多增量进行15~25次迭代求解。在求解阶段,计算机接受并求解有限元方法产生的方程组,ANSYS有多种求解系统方程组的方法,为了保证计算质量、稳定和求解速度,选用稀疏矩阵直接求解法,该方法是建立在与迭代法相对应的直接消元法的基础上的。为了全面了解鼓形齿齿面承载后的应力、应变情况,从鼓形齿承载后的变形、米塞斯等效应力、接触状态、接触应力等几个方面分析鼓形齿的齿面情况。根据材料力学相关知识,该型号鼓形齿联轴器所用材料应选择第四强度理论作为相对应的准则即范·米塞斯屈服准则,米塞斯等效应力:
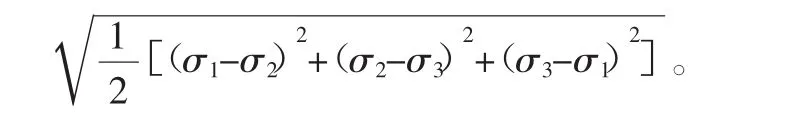
其中,σ1、σ2、σ3分别为第一、第二、第三主应力。
利用ANSYS软件求解出的接触应力和米塞斯应节力分布云图如图5、图6和图7所示。

图5 鼓形齿面接触应力

图6 外齿轴套米塞斯应力

图7 内齿圈米塞斯应力
由图5~图7可知:当GCL13型鼓形齿联轴器压力角大小为20°时,位移圆半径分度圆直径之比R/d=0.828,齿顶高系数:0.8,=1.1,=0.8,=0.85,在两轴线对中工况下,鼓型齿面上的接触应力大小及分布如图5所示,最大接触应力为340.84 MPa;外齿轴套米塞斯应力的大小及分布如图6所示,最大的米塞斯应力为213.552 MPa;内齿圈米塞斯应力大小及分布图如图7所示,最大米塞斯应力为222.472 MPa。
3 性能规律分析
3.1 改变位移圆半径的影响
取R/d=0.828,0.9,1.0三种情况来探索位移圆半径对鼓形齿联轴器力学性能的影响。
1)位移圆半径R=265 mm(R/d=0.828),参见本文第2节分析。
2)位移圆半径R=288 mm(R/d=0.9)如图8、图9和图10所示。

图8 鼓形齿面接触应力

图9 内齿圈米塞斯应力

图10 外齿轴套米塞斯应力
3)位移圆半径R=320 mm(R/d=1)如图11、图12和图13所示。

图11 鼓形齿面接触应力
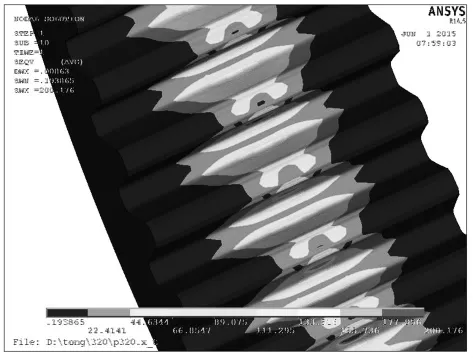
图12 内齿圈米塞斯应力

图13 外齿轴套米塞斯应力
4)位移圆半径变化与应力变化关系。在两轴线对中工况下,GCL13型鼓形齿联轴器的位移圆半径变化与应力变化关系如表1所示。
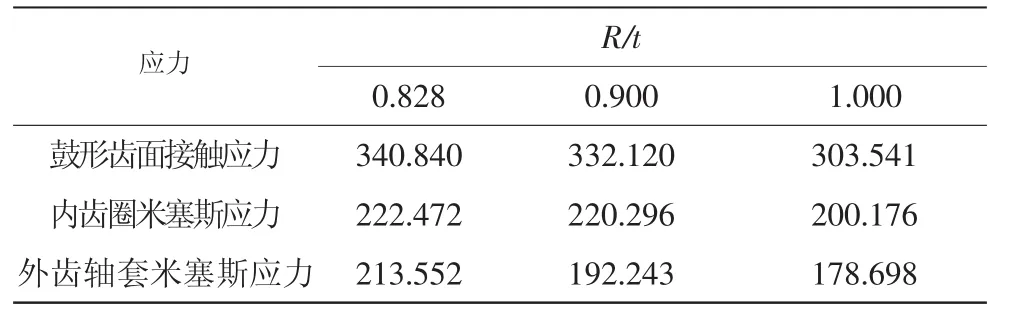
表1 位移圆半径变化与应力变化关系MPa
由表1可以看出,在轴线对中工况下,对于GCL13型鼓形齿联轴器,鼓形齿联轴器齿面接触应力、内齿圈米塞斯应力和外齿轴套米塞斯应力会随着位移圆半径的增大而减少。此外,这些应力的分布规律以及最大应力出现的位置基本相同。

图14 鼓形齿面接触应力

图15 内齿圈米塞斯应力

图16 外齿轴套米塞斯应力

图17 鼓形齿面接触应力
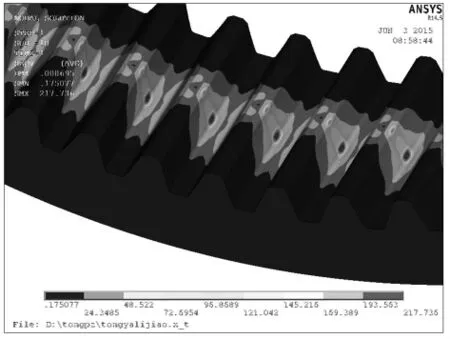
图18 内齿圈米塞斯应力
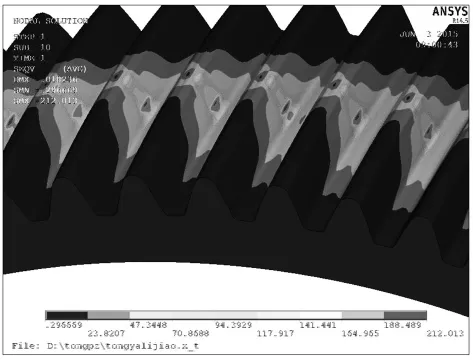
图19 外齿轴套米塞斯应力
3.2 改变压力角的影响
为了研究压力角的影响,选取压力角分别为20°、22°和24°进行分析。
1)压力角大小为20°,参见第3节分析。
2)压力角大小为22°,如图14、图15和图16所示。
3)压力角大小为24°,如图17、图18和图19所示。
4)压力角与应力变化关系。在两轴线对中工况下,压力角变化与应力变化关系如表2所示。
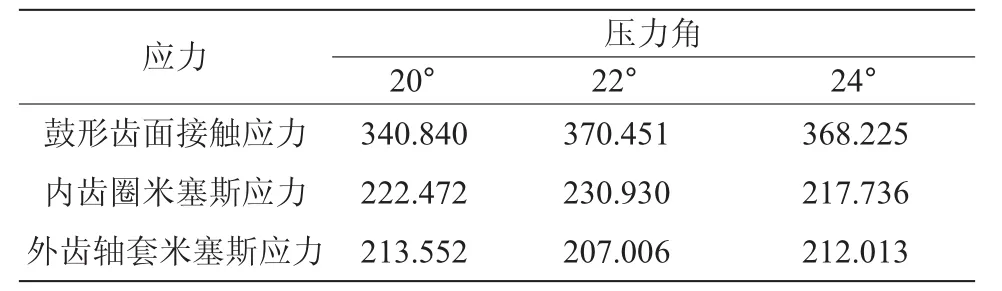
表2 压力角与应力变换关系 MPa
由表2可以看出,在轴线对中工况下,对于GCL13型鼓形齿联轴器,压力角的大小对鼓形齿联轴器齿面接触应力、外齿轴套米塞斯应力以及内齿圈米塞斯应力大小和分布位置的影响很小。
4 结语
1)鼓形齿联轴器的承载性能受其齿形参数的影响较大。在轴线对中工况下,对于GCL13型鼓形齿联轴器,随着位移圆半径的增大,鼓形齿联轴器承载能力会有所提高;压力角的大小对鼓形齿联轴器齿承载能力影响很小。
2)压力角和位移圆半径两个齿形参数的变化对不同型号的GCL型鼓形齿联轴器承载性能的影响规律不完全相同。
[1] 易传云.鼓形齿联轴器啮合分析[J].上海大学学报(英文版),2005,9(6):61-67.
[2] 张勇,谢剑刚,王宏波.鼓形齿接触应力的有限元分析[J].机械,2005(4):7-9.
[3] 毕青.搅拌机用鼓形齿联轴器的全齿有限元接触分析[D].上海:上海交通大学,2009.
[4] 孟百刚.鼓形齿联轴器的应用与设计[J].一重技术,2002(增刊1):19-22.
[5] 王庆五,左昉,胡仁喜.ANSYS10.0机械设计高级应用实例[M].北京:机械工业出版社,2006.
[6] 高耀东,刘学杰.ANSYS机械工程应用精华50例[M].北京:电子工业出版社,2011.
[7] 机械设计手册编委会.机械设计手册:第1卷[M].北京:机械工业出版社,2004.
[8] 刘自然,何园园,张跃春,等.鼓形齿联轴器主要参数探讨及应用研究[J].机械工程师,2012(8):75-76.
[9] 郝好山,胡仁喜,康士廷,等.ANSYS10.0机械设计高级应用实例[M].北京:机械工业出版社,2006.
[10] 宋乐民.齿形与齿轮强度[M].北京:国防工业出版社,1987.
[11] 约翰逊.接触力学[M].北京:高等教育出版社,1992.
[12]邓平凡.ANSYS12有限元分析自学手册[M].北京:人民邮电出版社,2011.
