定式思维招全错，审清题意挽败局

王修汤

学完《简单的线性规划问题》一节后，我班同学练习了这样一道题.

一、题目重现

某制药公司有三条生产线生产中成药产品.公司进行产品结构调整，决定用现有产品生产线的剩余生产能力试生产两种新产品，新产品的生产方式为批量生产：400个产品为一批.目前由于大多数生产设备已用于其他产品的生产，所以首先确定每周生产线可用的生产时间，以及各种产品每批的生产时间，时间单位以小时计.然后由生产中心确定生产成本，市场中心进行定价，得到两种新产品每一批的利润.具体数据如下表所示.

试确定这两种产品的生产方式，以使公司每周的利润最大，并求出最大利润.

二、普通解法我班同学普遍解法如下：设每周生产产品一x批，生产产品二y批，每周的利润为g千元，则约束条件为

目函数为z=3x+5y，画出可行域（如图1）.当直线z=3x+5y经过直线3x+2y=18与直线y=6的交点（2，6）时，z取最大值36，所以生产线每周生产2批产品一，生产6批产品二时，公司利润最大，最大利润为36千元.

三、参考答案

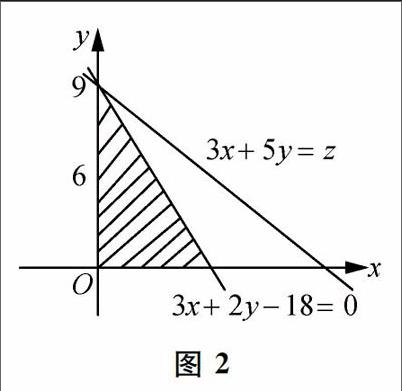
设第三条生产线每周生产产品一、产品二分别为x批、y批，此生产线每周的利润为z元z千元，则约束条件为3x+2y≤18，x≥0，y≥0目标函数为z=3x+5y，画出可行域（如图2）.当直线z=3x+5y经过直线3x+2y=18与直线x=0的交点（O，9）时，z取最大值45，所以生产线1每周生产4批产品一，生产线2每周生产6批产品二，生产线3每周生产9批产品二时，公司每周的利润最大，最大利润为87千元.

四、错因分析

本是课本上的一道常规练习题，全班同学却无一人做对，这必须引起足够的重视.仔细分析了解就会发现，是我们的定式思维招致了错误.因为这几天我班刚学过线性规划的应用题，很多题目都是根据条件列jLI_I表格，再写出约束条件.例如课本中有一道例题：某工厂生产甲、乙两种产品，生产1 t甲种产品需要A种原料4 t，B种原料12 t，产生的利润为2万元；生产1t乙种产品，需要A种原料1t，B种原料9t，产生的利润为1万元.现有库存A种原料10t，B种原料60t，则甲、乙两种产品应各生产多少，才能使利润总额最大？

课本上为了指导解题，将已知数据整理成下表：

根据表格，很多同学列出的约束条件是O≤4x+y≤10，0≤12x+9y≤60，这个约束条件对于这道x≥0，y≥o.题来说是正确的.但是当我们做其他题目时，例如前面的原题，还不由自主地去套用表格的这种模式，就会列出上面错解中的约束条件.从错解得出的结论也能发现错误，因为错解结论中并没有交待清楚每一条生产线如何生产，仅仅是笼统指出生产线每周生產2批产品一，生产6批产品二.

五、重新审题

题目中“400个产品为一批”是什么意思？每一批只能全是一种产品吗.还是可以在同一批中同时有产品一和产品二？静心分析应该是每一批都是一种产品.第一，因为生产线的性质决定了每批只能生产一种产品；第二，题目中的表格也体现出每批只是一种产品.

对于第1条和第2条生产线，没有悬念.每周只能生产一种产品，当然尽全力生产，效益最高.所以第1条生产线每周生产4小时产品一，即生产4÷1=4批，就能获得最大利润4×3=12（千元）；而第2条生产线每周生产12小时产品二，即生产12÷2=6批，就能获得最大利润6×5=30（千元）.

唯独第3条生产线，它是一段时间生产产品一，另一段时间生产产品二，必须合理安排才能获得更大的利润.所以才会有约束条件3x+2y≤18，x≥0，y≥0其实从表格可知，产品二所需时间短，利润大，所以理所当然全部生产产品二，这和我们利用线性规划知识解得的答案r=0，y=9完全一致.所以，第3条生产线每周生产18小时产品二，即生产18÷2=9批，获利9×5=45（千元）.总的利润为每周12+30+45 =87（千元），即8.7万元，

由此算来，解题的前提是“审题”，如果连题目的意思都没有弄明白就下手解题，那就只能死套题型，最终招致的就是“全错”.只有审清题意，才是解决数学问题的“正道”，endprint