基本不等式的历史背景及几何意义

杨志文

1.赵爽的“弦图”

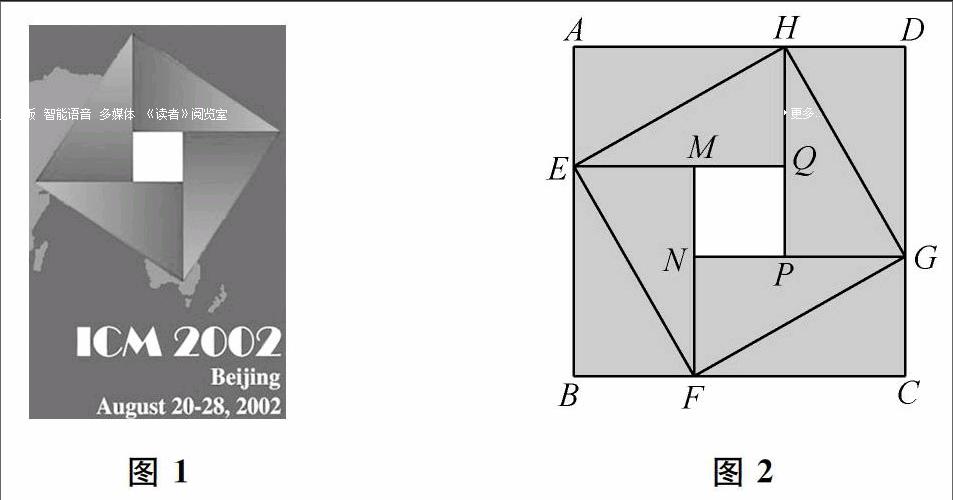
我们先来看一张图片，2002年第24届国际数学家大会在我国召开，图1是大会会标，是根据我国古代数学家赵爽的“弦图”设计的.

公元3世纪，中国数学家赵爽“负薪余日，聊观《周髀》”，他在给<周髀算经》“勾股网方图”作注时，给出图2所示的“大方图”.赵爽写道：

“以图考之，倍弦实，满外大方，而多黄实.黄实之多，即勾股差实.以差实减之，开其余，得外大方.大方之面，即勾股并也.”

用数学符号语言表达，即：若直角三角形两直角边为为a，b，a≥0，b≥0，则

（a+b）²=4ab+（b-a）²，（a+b）²=2c²-（b-a）2=2（a²+b²）-（b-a）²，

因此，可得不等式4ab≤（a+b）²≤2（a²+b²）.

2.歐几里得的矩形之变

古希腊数学家似乎并没有对各类中项的大小进行比较，但他们已经研究过部分中项的几何作图法以及它们之间的数量关系，欧几里得在《几何原本>卷六命题13中给出了两条已知线段之间的几何中项的作图法.如图3，以AB为直径作半圆ADB，则CD即为AC和CB之间的几何中项.

3.芝诺多鲁斯的等周问题

在欧几里得之后，获得与均值不等式等价结果的数学家是芝诺多鲁斯（Zenodorus，约公元前2世纪）.他写了一本名为《论等周图形》的书，专门研究等周问题.在书中，他给出了许多命题，其中一个是：“在边数相同、周长相等的所有多边形中，等边且等角的多边形的面积最大.”

这些历史材料，再现了基本不等式的“源头”，通过挖掘数学历史文化背景，揭示了基本不等式的几何意义，值得我们细细品味.endprint