利用双链DNA 编码节点和质粒求解的有向Hamilton 路径问题

沈成才 甄 涛 廖 峰

（北京师范大学克拉玛依附属学校 新疆克拉玛依 83400）

0 前言

DNA计算以DNA 碱基序列作为信息编码的载体，利用现代分子生物学技术，在试管内控制酶的作用下进行DNA 的序列反应，作为实现运算的过程，以反应前DNA 序列作为输入数据，完成运算后，从反应后的产物及溶液中得到全部的解空间。由于DNA 计算具有高度的并行性和较大的存储量，可以大规模并行处理和组合运算，解决算法研究领域的某些难解问题，如Hamilton 路径问题（Hamilton Path Problem，HPP）。Hamilton 路径是指在有向图中开始于起点，结束于终点，且一次性经过所有节点的最短路径。用寡聚核苷酸片段编码图的顶点和边，放入溶液进行生化反应，生成表示随机路径的DNA，再通过PCR、凝胶电泳、亲和纯化等操作，完成解的产生和最终解的分离，如果有经过图的所有顶点一次且只经过一次的最短DNA 序列，则得到Hamilton 路径，否则就不存在。Hamilton 路径在互联网、交通网、通讯网、集成电路、DNA 计算机及国民经济各行各业等都有重要的应用前景［1］。

Adleman 利用DNA 编码等分子生物技术解决了有向图中的Hamilton 路，Nobuhiko Morimoto 等给出了该问题的表面计算方式，Masanori Arita 等基于双链DNA 比单链DNA 结构稳定且不易形成二级结构，设计了一种双链DNA 分子的HPP 模型，刘文斌、许进提出赋权Hamilton 路径的DNA计算模型［2］。高琳等人通过编码合成ssDNA（Single Strand DNA）片段研究基于分子生物技术的有向最短哈密尔顿路问题的DNA 算法，也有一些研究基于质粒DNA 计算模型的DNA 计算、Hamilton 圈问题的DNA算法等［3］。

可见，Hamilton 路径问题的研究大多建立在以单链DNA 编码节点的方式上。而对于Hamiltion路径问题，DNA 计算在可行解的生成过程中，错误杂交、顶点较多等因素，较多的单链寡聚核苷酸片断可能会形成发夹结构，产生大量“伪解”，制约模型的应用规模；另外，DNA 计算所应用的生物技术也存在着误差，例如PCR 技术中的聚合酶的碱基错配率，随着循环次数的增加，带有错配碱基的拷贝数增加，偶尔一些非酶的非受控制的支路的反应，甚至包括DNA 链的动力分解，均增大了最优解输出的难度［4］。

为了减少错配的可能，提高筛选Hamilton 最短路径的有效性，本研究以具有黏性末端的改造质粒DNA 作为框架，利用双链DNA 编码节点，对生成的各种路径进行筛选，保留Hamilton 最短路径。

1 Hamilton 路径的DNA 算法及算法实现

1.1 问题描述 设图G 是一个有向图，其指向输入和输出顶点分别为vin 和vout。如果一条从vin 到vout 路包含G 的每个顶点一次且仅有一次的一条有向路P 称为有向Hamilton 路问题，简称HPP 问题。

有向Hamilton 问题的非确定性解法步骤如下：

1）产生经历有向图节点的所有路径。

2）只保留起点是vin，终点是vout 的路径。

3）保留只有n 个节点的路径。

4）保留那些进入有向图中所有节点至少一次的路径。

5）如果有任何路径保留下来，则存在Hamilton 路径。否则，不存在［5］。

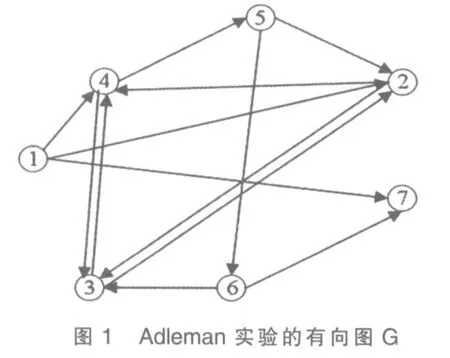
1.2 算法及实现

1.2.1 编码设计 用30 bp 的DNA 双链进行编码；对关联的各条边编码，取前节点的后半段序列作为边的前半段编码，取后节点的前半段序列作为边的后半段编码；将编码的各边通过化学合成法合成。

例如顶点①的编码为TATCGGATCGCGATC

ATAGCCTAGCGCTAG

顶点③的编码为GCTATTCGAGACGTC

CGATAAGCTCTGCAG

顶点④的编码为GGCTAGGTACGATCG

CCGATCCATGCTAGC

例如：各边的编码

①—③GGATCGCGATCGCTA

CTAGCGATAAGCTCT

③—④TTCGAGACGTCGGCT

GCAGCCGATCCATGC

①—③—④

GGATCGCGATCGCTATTCGAGACGTCGGCT

CTAGCGATAAGCTCTGCAGCCGATCCATGC

1.2.2 质粒DNA 的构建 质粒是染色体外能够独立复制，稳定遗传的一种环状双链分子，包含复制子、选择性记号和克隆位点。根据Hamilton 路径的长度，选用容量合适的质粒，通常选用PBR322型或PUC 系列载体。利用限制性内切酶对质粒DNA切割，形成2 个分别与Hamilton 路径中的起点和终点边编码相互补的黏性末端。然后对其进行扩增，测其长度标注为n。由于其具有能和起点边和终点边编码相互补且唯一互补的黏性末端，所以通过质粒可以选出从起点到终点的所有路径，排除了其他可能路径。

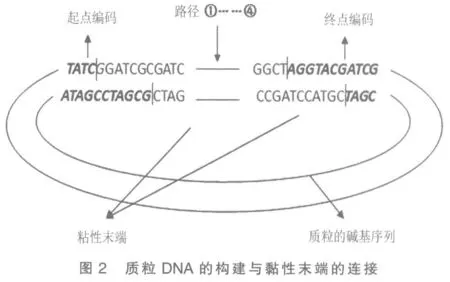
1.2.3 路径生成 使外源DNA 与质粒载体发生一系列连接反应，生成各条有向路径。通过合成扩增大量的编码片段，可以获得从起点到终点的所有可能路径。

1.2.4 电泳分离重组质粒 各条路径会和载体质粒发生结合而形成闭环DNA 分子，也有部分载体未发生结合而成开环。可以通过与标准目的重组质粒进行电泳条带对比分析进行筛选，利用琼脂糖凝胶电泳分离重组质粒。

1.2.5 PCR 与测序 通过利用构建载体时的限制性内切酶对重组质粒进行切割；将插入的路径切割下来，并进行PCR 扩增，有利于进一步筛选。最后，通过对路径中的碱基序列测定，分离出经各节点一次的路径，即为最短Hamilton 路径。

2 算法分析与讨论

线性单链DNA 合成简单、操作性强，但是单链DNA 稳定性差，在反应过程中容易发生错配，产生伪解，且其筛选方法是在扩大生成的起点到终点路径下进行，并不能排除其他解，加大了后续测序难度。与线性DNA 相比，质粒DNA 在限制酶剪切之后，又迅速连接成环状分子，从而确保计算过程免受其他酶的干扰，计算准确性高且稳定。质粒始终是双链结构，不会形成发夹结构，方便切割操作，便于使用凝胶电泳技术检测结果。复制和转录过程中，DNA 不被分裂成长的单链，而是DNA的少部分被打开并被相关蛋白质周密地控制，阻止无法预料到的退火形式［6］。

因此，本研究利用双链DNA 编码节点和质粒DNA，以求获得最短有向Hamilton 路径。一方面，通过DNA 双链对节点编码，形成有双链DNA 组成的各条有向边。单链DNA 是平末端连接，DNA双链则是黏性末端连接，且稳定性好，有助于提高边与边的连接效率，减少在路径生成过程中的分子间错配，从而提高准确性；另一方面，从起点到终点路径，先利用相应引物进行PCR 扩增，使对应的路径大量增加，再用凝胶电泳将一些非起点到终点路径而与目的片段相同大小的路径分离出来，加大了测序难度。而利用质粒进行筛选时，质粒可以特异性的和起点到终点的路径结合，然后对目的大小的重组质粒进行凝胶电泳分离，再进一步扩增，这样便排除了非起点到终点路径，可以有目的性地对可行解进行集中分离，避免标本在扩增中的浪费，使筛选效率得以提高。