应用统计学原理对多倍体配子及杂交子代比例问题的研究

何金华 王爱民

（1 江苏省滨海中学 江苏滨海 224500 2 江苏师范大学生命科学学院 江苏徐州 221116）

孟德尔遗传定律揭示了杂交的本质，解释了个体产生配子的过程和结果，从细胞学基础上奠定了遗传的基本规律。在现行高中教材中，对1 对或多对等位基因的杂交过程进行了比较详尽的说明，但对多倍体的杂交或自交的原理与过程的介绍较少，仅在染色体变异及三倍体无籽西瓜的育种过程中进行归纳总结。有研究表明，对1 种基因座多倍体产生的配子问题不仅可以通过图解法、图示法、组合法进行计算［1］，还可以通过“二价体”的假设进行，即以其中的2 对1 种基因座染色体为基础，多出来的染色体以“随机”的方式分别插入二价体产生的配子中，以获得最终产生的配子比例［2］。但上述方法没有对子代的比例及基因型问题进行数学分析，因此本文在上述研究的基础上作进一步探索。

1 多倍体的概念

由受精卵发育而成的个体，体细胞中含有2个染色体组的称为二倍体，体细胞中含有3 个或3 个以上染色体组的称为多倍体［3］。多倍体在自然界中分布极为广泛，例如普通小麦、烟草等。常见的多倍体植物又分为1 种基因座多倍体和2 种基因座的多倍体，例如八倍体小黑麦即为2 种基因座的多倍体。

2 1种基因座多倍体产生配子及子代比例

在一般情况下，多倍体产生配子的过程较为复杂，例如1 种基因座重组是不同类型2n 配子杂合性差异的重要原因［4］，2 种基因座的三倍体百合雄性不育可能会影响子代的比例问题等［5］。本研究所论述的基础为在理想状态下进行，即不考虑基因突变、基因重组等因素。

2.1 1种基因座的多倍体产生配子的比例 对于二倍体生物而言，产生的配子比较简单，例如Aa 产生的配子即为A 和a，比例为1∶1。若以1 种基因座四倍体AAaa 为例，则需要进一步细化产生的配子比例关系。

2.1.1 以减数分裂为基本原理的推导过程 在减数分裂过程中，同源染色体彼此分离、非同源染色体自由组合。因此，对于AAaa 的细胞来说，具有6 种组合方式，如图所示：

若第1 条A 和第2 条A 组合，则产生的配子有AA 和aa 2 种各2 个。

若第1 条A 和第3 条a 组合，则产生的配子有Aa 和Aa 2 种各2 个。

若第1 条A 和第4 条a 组合，则产生的配子有Aa 和Aa 2 种各2 个。

若第2 条A 和第3 条a 组合，则产生的配子有Aa 和Aa 2 种各2 个。

若第2 条A 和第4 条a 组合，则产生的配子有Aa 和Aa 2 种各2 个。

若第3 条a 和第4 条a 组合，则产生的配子有aa 和AA 2 种各2 个。

经过分析可以知道，总共有6 种组合，产生的配子有24 个，其中AA 占1/6，aa 占1/6，Aa 占4/6。AA∶Aa∶aa＝1∶4∶1。

2.1.2 以统计学为基本原理的推导过程 上述将全部组合写出后进行统计的方法明显比较复杂，因此不妨从统计学角度进行分析。目前高中学生已经学习了统计学中排列组合的基本知识，因此可以由此入手。

以上述1 种基因座的四倍体AAaa 自交为例。

第1 类方法如下：

从AAaa 中可以知道，配子应该是2 个字母的组合，即有3 种：AA、aa 和Aa。现在以______ 和_____ 作为填空题进行作业。在这里，需要提醒的一个问题是，AAa 产生的A 概率为2/3，而Aaa 产生A 的概率为1/3，要注意这个概率的算法。

现统计AA 的概率，按照上面所说的注意问题，AA=2/4×1/3×1=1/6 （备注：2/4 是取第1 个A的概率，1/3 是取第2 个A 的概 率，1 是AA 只有1 种组合方式）；同理统计aa 也为1/6；Aa 的计算方法为：Aa=2/4×2/3=1/3，aA=2/4×2/3=1/3，因此Aa=2/3。因此，AA∶Aa∶aa＝1∶4∶1。

第2 类方法如下：

可以从种类的角度分析，例如，产生Aa 这种配子，A 为2 个中取1 个，a 为2 个中取1 个，因此Aa=C12×C12=4 种；AA=C22=1 种，aa=C22=1 种，因此，比例仍然是AA∶Aa∶aa=1∶4∶1。

故，AA 占1/6，aa 占1/6，Aa 占4/6。此方法比第1 种方法简单和简便，便于学生掌握运用。

如果以AAaaaa 为例，运用上述的统计学原理，利用第1 类方法可以计算得到AAa=2/6×1/5×1×3=1/5（说明：第1 个2/6 是取A 的概率，剩余5个后取第2 个A 的概率为1/5，最后剩下4 个a，因此再取1 个a 的概率为1，最后乘以排序的3种方式，这里需要注意的是，3 种排序可以直接写出，也可以通过A33/A22计算得到）；同理，aaa=4/6×3/5×2/4=1/5；Aaa=2/6×4/5×3/4×3=3/5。第2 种计算方法为：配子种类总共有C26=20 种，其中每种类 型 的 比 例 为Aaa=C12×C24=12 种，aaa=C34=4 种，AAa=C22×C14=4 种，比例为Aaa∶aaa∶AAa=3∶1∶1。

结论： 由上面的2 种计算原理和2 类计算方法可以看出，以组合运算公式计算的过程较为简单且易于理解，是讨论使用的常用方法之一。

2.2 1种基因座的多倍体产生子代的计算方法为进一步简便说明子代的计算方法，以先进行基因型比例的计算，再进行表现型比例的计算。

2.2.1 基因型的比例计算 基因型的比例计算可以分成2 种算法，第1 种按照原始的棋盘法进行，第2 种按照统计学原理进行。

第1 种：按照原始的棋盘法进行。

根据上面所计算得到的配子种类，可以按照棋盘法的原则进行统计分析，对于AAaa 的基因型的计算如表1所示：

?

由此表可知，基因型的比例为AAAA∶AAAa∶AAaa∶Aaaa∶aaaa=1∶8∶18∶8∶1。

第2 种：按照统计学原理进行。

在棋盘法中，配子形成受精卵的方式类似于数学中的平方和公式，即（AA∶Aa∶aa）2=（1∶4∶1）2，展开即可得到结果。根据排列组合的规律可知，最后形成的受精卵的基因型中的显性基因分别有4个、3 个、2 个和1 个。由于AA=1/6，Aa=4/6，aa=1/6，因 此AAAA=1/36，AAAa=8/36，AAaa=18/36，Aaaa=8/36，aaaa=1/36。因 此，AAAA ∶AAAa ∶AAaa ∶Aaaa ∶aaaa=1∶8∶18∶8∶1。

在该结果中，可以明显发现一个规律，即左对角线为同1 种基因型，且比例为正态分布的顶点，如图2。

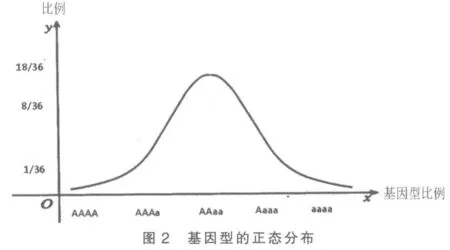
2.2.2 表型的讨论 一类是A 基因具有累加效应，即随着A 个数的增加，表型不同，因此表型比例为AAAA∶AAAa∶AAaa∶Aaaa∶aaaa=1∶8∶18∶8∶1。另一类是没有累加效应，即表型和A 个数没有关系，因此显隐性的比例是35∶1。

结论： 基因型比例可以应用平方和公式展开计算，且如果亲代基因型为对称类型（例如AAaa）则子代基因型符合正态分布。

3 2 种基因座的多倍体产生配子及子代比例

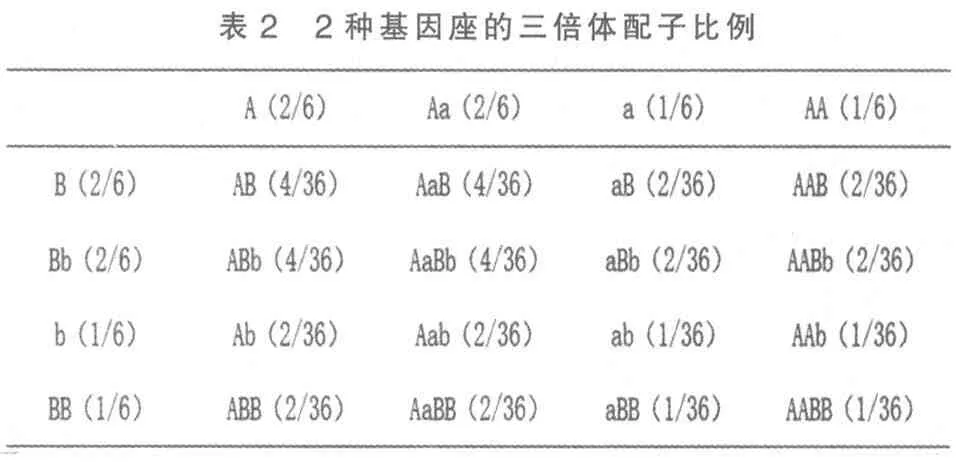
3.1 2种基因座的多倍体产生配子比例 除前面所述的以减数分裂、图例法和“二价体”方法进行的研究外，还可以直接采用乘法分配律的方法进行。2 种基因座的多倍体可以看成是1 种基因座的随机交配，即本质含义是将2 种基因座进行拆解后组合。例如，三倍体AAaBBb 可以分为AAa和BBb 配子的杂交，应用上面的组合运算方式即可求得AAa 产生的配子为A∶Aa∶a∶AA=2∶2∶1∶1，即共产生4 种配子，比例为A=Aa=2/6，a=AA=1/6，B∶Bb∶b∶BB=2∶2∶1∶1，即共产生4 种配子，比例为B=Bb=2/6，b=Bb=1/6。可以知道，配子种类有4×4=16 种，如果要计算每种比例和比值可以从配子的比值相乘得到，例如，AB=4/36，依次类推。

?

表2所列出的是16 种配子的比例，由于部分配子在发育过程中可能因染色体缺失而产生致死现象，因此三倍体产生的子代可能是很多种类型，有可能产生正常或者配子类型，所以三倍体生物存在高度不育的情况。

3.2 2种基因座的多倍体产生子代的计算方法无论是1 种基因座多倍体还是2 种基因座的多倍体，最终都是由配子结合产生受精卵发育形成的。在2 种基因座的多倍体计算中，由于配子比例较多，因此，所形成的受精卵的比例就更多。以上述例子为例，配子有16 种，从理论上讲，受精卵有16×16 种组合方式。

为便于说明问题，再以AAAaBbbb 为例进行演示。首先进行拆解：AAAa 产生的配子有AA=Aa=1/2，Bb=bb=1/2；其次再进行组合：

?

从表3可以看出，AAAaBbbb 产生的配子为AABb∶AaBb∶AbBb∶Aabb=1∶1∶1∶1。

?

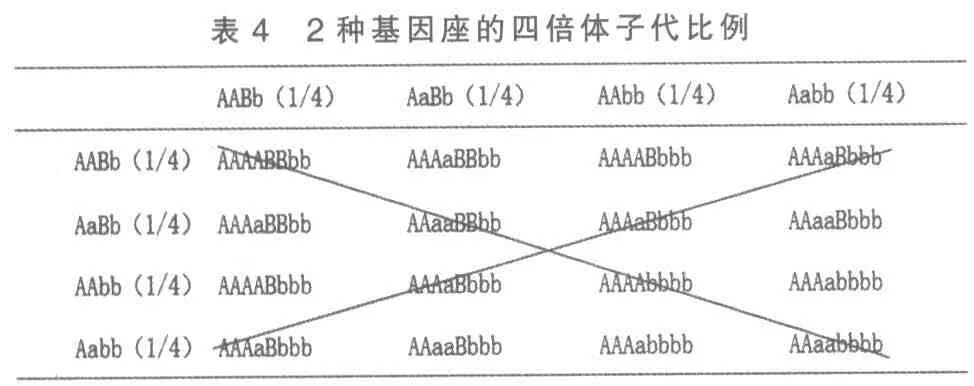
由表4可知，2 条对角线上的基因型分别是4个1 种和1 个4 种，其余基因型都为2 个，具体基因型的比例为AAAABBbb∶AAAaBBbb∶AAAABbbb∶AAAaBbbb∶AAaaBBbb∶AAaaBbbb∶AAAAbbbb∶AAAabbbb∶AAaabbbb=1∶2∶2∶4∶1∶2∶1∶2∶1∶2。如果将其中比例顺序作调整，可以得到比例为1∶1∶2∶2∶4∶2∶2∶1∶1，即呈现正态分布，且比例最高的是左对角线部分。

综合表1和表4可以推知，在进行基因型比例推测时候，左对角线部分比例最高，为正态分布的顶点，右对角线部分比例始终为一份，其余部分的基因型呈对称分布。表型的比例依据基因型可以得到具体结果。

4 总结

从上面的探索过程中发现，多倍体自交的过程相比二倍体要复杂得多，随着染色体组数目的增加，产生的配子种类、子代基因型比例和表型比例大幅增加，计算过程也较为繁琐。当然，这里所论述的是进行解题的过程、方法和思维，对于大数据的计算不必深入探究。

解决多倍体子代的基因型与表型的核心在于计算产生配子的种类和比例，而配子的种类和比例的计算则依靠组合运算方式。涉及1 种基因座的多倍体（AAaa）配子采用“先写种类后计算概率及比例”的方法，涉及2 种及以上染色体的多倍体（AAaBBb）配子采用“拆分组合再写出配子概率及比例”的方法。基因型的计算则依靠配子的种类和比例进行计算，且无论配子比例为多少，利用棋盘法即可得到左对角线比例最高，右对角线比例为1 份，其余基因型比例对称分布。表型根据基因型的种类和比例进行推算。

以上探索过程仅从理论方面对1 种基因座多倍体产生的配子和子代比例进行研究，而实际过程则复杂得多。刑少辰等［6］研究表明，1 种基因座多倍体自交产生的后代绝大部分会保留其原来的倍性，但会有个别的变化，甚至会出现二倍体，李云等［7］研究发现水稻1 种基因座三倍体与二倍体F2杂交后代出现非整倍体和二倍体个体产生，且二倍体自交后性状表现稳定。

马斯洛的需求理论表明，人的发展需求是最高的需求。因此，在教学实践过程中，更要注重对学生思维能力发展的培养，注重对探究过程的教学，以此启发智慧、启迪灵魂，塑造真正意义上的“素质教育”，培养一代教育“新人”。