基于单向LOCC的正交两体态区分算法
2018-03-03司萌萌李志慧刘成基
司萌萌,李志慧,刘成基
(陕西师范大学 数学与信息科学学院,西安 710119)
0 概述
随着量子信息理论的发展,量子密码学相比经典密码学越来越体现出更多优势的同时,也提出了许多挑战性的课题[1-3],其中量子态的局域区分就是量子通信领域一个基本问题。在局域操作和经典通信(Local Operation and Classical Communication,LOCC)的限制下,正交态并不是总可以精确区分的[4-6]。一组正交量子态不一定可局域区分,是量子非局域性的一个表现。研究区域区分的规律不仅有利于理解量子非局域性,还可使人们能从新的角度去研究其他的量子信息理论问题[7-9]。两体正交量子态的局域区分方案如下:在许多可能的正交两体量子态中选出一个分发给Alice和Bob,他们只利用LOCC就可以找出他们共享的是哪一个态。文献[10]构造了一组乘积纯态,获得的结论是来自于不可扩张乘积基的成员之间是不能通过LOCC被完全区分的;文献[11]证明了任意2个多体正交纯态可以精确局域区分,此结果说明了在LOCC下量子态的纠缠与否与其精确区分的关系不大,也说明了此问题的复杂性;文献[12]的结果是得出了类Holevo上界对于局部的可访问的信息来自于一个两体系统的量子态系综;文献[13]的结果表明了几乎所有来自于N个d维多体系统的d+1个正交量子态集合通过LOCC是不可以完全被区分的。
近期,文献[14]提出了一个利用单向LOCC(one-way LOCC,1-LOCC)来区分两体正交态的框架,并在理论上给出了两体正交态的集合通过单向LOCC可区分性的判定,但文献[5]并没有给出区分两体正交态的一般性算法。本文给出基于单向LOCC的一类正交两体态区分算法,并在此算法的基础上,对4⊗4上的广义正交Bell态给出其可单向区分的一个充分条件,此充分条件可作为一个快速算法判断正交态是否可单向LOCC区分,最后对此结论给予实例验证。
1 文献[14]主要结论回顾
文献[14]得到了如下结果:在一个dA⊗dB的两体系统中,其中,dA、dB是子系统A和B的维数,如果第i部分(其中i=A或B)开始一个单向LOCC协议以完全区分一个正交两体态的集合,那么这样的一个单向LOCC协议存在的信息取决于一个di×di阶的Heimitian矩阵组成的子空间是否包含一个最大交换子空间。根据这一结论,对于dA⊗dB中的所有正交两体态集合,其单向LOCC的可区分性便可以得到判定[15]。
1.1 密度矩阵的谱分解
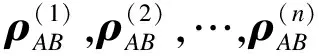
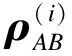
(1)
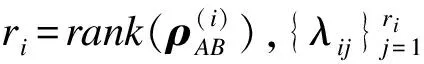
1.2 标准正交基和复矩阵
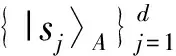
(2)

1.3 主要符号及说明
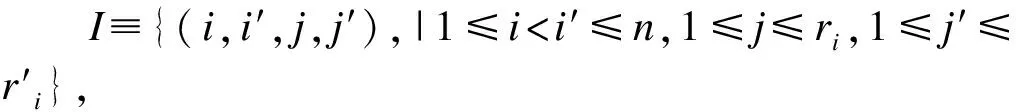
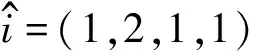
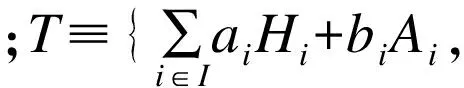
1.4 最大交换子空间
定义3如果实向量空间S中一个维数为d的子空间中的任意2个矩阵都可交换,那么这个子空间称作一个最大交换子空间(Maximally Abelian Subspace,MAS)。
注释1任意一个MAS和唯一一组共同的特征向量相对应,且这组共同的特征向量可以使得MAS中所有Hermitian矩阵在这组基下对角化。
1.5 d⊗d上的广义正交两体量子态
定义4在d⊗d中,d2维的广义的正交两体量子态可以表示为[6]:
(3)
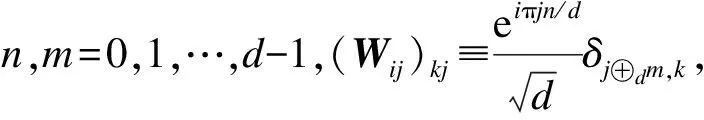
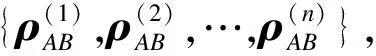
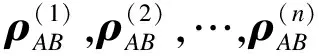

注释2设{Ti}d+ti=1是T⊥的一个MAS。令C是由矩阵{i[Tj,Tk]|1≤j (Γj)kj=iTr(Gj[Tk,Tl]) 本文主要考虑式(3)中的态在由Alice开始的单向LOCC可区分问题。现给出在d⊗d中,任意N(2≤N≤d2)个纠缠态的局域区分算法。 步骤1在d⊗d上任意选取N(2≤N≤d2)个纠缠态。 步骤3计算dimT⊥,作如下判断: 1)当dimT⊥≤d-1时,该N个态不能由Alice开始一个单向LOCC协议来区分,算法终止。 2)当dimT⊥=d时,进一步检查:该T⊥是否为一个MAS。 如果是,则该N个态可以由Alice开始一个单向LOCC协议来区分,转入步骤4;否则,算法终止。 3)当dimT⊥≥d+1时,进一步检查:如果T⊥包含一个MAS在S中,那么该N个态可以由Alice开始一个单向LOCC协议来区分,转入步骤4;否则,算法终止。 步骤4计算MAS中非单位矩阵的特征向量。 注释3若步骤1中的N个态可单向LOCC区分,则以上算法求得的MAS的特征向量便可作为相应的投影算子对所选的纠缠态进行区分; 步骤3中,由dimT⊥=d2-dimT得到T⊥的维数,基于T⊥的维数值,可以将这些正交两体态分成不同类。 该算法是判断正交两体态是否可单向LOCC的一般性算法,虽与文献[14]算法性能相似,但却优于原算法,其原因是本文算法适用于任何一组正交两体态是否可区分的判定;其次,该算法将判断正交态是否可区分转化为判断正交态组的正交补空间是否包含有一个MAS,区分时只需进行一次投影测量,该算法同时兼顾了算法复杂度和算法性能,因此,更具有实际应用价值。 利用2.1节算法,对式(3)中d=4的情况,得到快速判断纠缠态单向LOCC课区分的一个结论。 由式(3),当d=4时,4⊗4上广义的正交两体态为: (4) 令集合: 定理1对式(4)中的广义正交两体态,设其正交补空间为T⊥,若T⊥⊃Ui(i=1,2,…,6),则这组正交两体态一定可单向LOCC区分。 考虑集合: 计算i[Ti,Tj](i,j=1,2,…,5)可得,C是由矩阵G1和G2张成的,其中: R是由矩阵Ω1和Ω2张成的,其中: 矩阵Ω1和Ω2是秩2的且Supp(Ω1)∩Supp(Ω2)是由(0,0,0,0,1)T张成的。 因此,由引理2,U1包含一个MAS,又U1⊂T⊥,因此T⊥包含一个MAS,从而由引理1可知,对应的这组纠缠态可单向LOCC区分。 其他情况可类似证明。 注释4实际上,Ui(1,2,…,6)中包含一个MAS,且涵盖了了由T可能组成的所有含MAS的集合。因此,一组纠缠态对应的T⊥若包含其一,该T⊥就包含一个MAS,这些纠缠态就一定可单向LOCC区分。 当然,利用2.1节算法也可以区分式(4)中的态,但判断T⊥是否包含一个MAS有时是困难的。 步骤1在4⊗4上任意选取N(2≤N≤16)个纠缠态。 步骤3根据T⊥作如下判断: 1)若T⊥满足定理1,则该N个态可以由Alice开始一个单向LOCC协议来区分,转入步骤4。 2)若T⊥不满足定理1,则该N个态不可以由Alice开始一个单向LOCC协议来区分,算法结束。 步骤4计算MAS中非单位矩阵的特征向量。 因此本文提出的算法计算复杂度较小,给纠缠态的区分带来了方便。 基于以上快速算法(3.2节),现给出实例验证。 例2判断4⊗4上的一组纠缠态{|ψ01〉,|ψ10〉,|ψ11〉,|ψ23〉}是否可单向LOCC区分。 因此,T⊥是由: 生成。 符合定理1,因此该4个态一定可单向LOCC区分。 接下来讨论如何区分这组态。通过计算[Tj,Tk](j,k=1,2,3,4,5,6,7): [T1,T2]=0,[T1,T3]=0,[T1,T4]=0 [T1,T5]=0,[T1,T6]=0,[T1,T7]=0 [T2,T3]=0,[T2,T4]=0,[T2,T5]=0 [T2,T6]≠0[T2,T7]≠0 [T3,T4]=0,[T3,T5]≠0,[T3,T6]≠0 [T3,T7]≠0 [T4,T5]≠0,[T4,T6]≠0[T4,T7]≠0 [T5,T6]≠0,[T5,T7]≠0;[T6,T7]=0 故T⊥包含的MAS集合为: 分别记为γ1、γ2、γ3、γ4。 因此: 显然,{|ψ01〉,|ψ10〉,|ψ11〉,|ψ23〉}可单向LOCC区分。 基于文献[14]利用单向LOCC区分两体正交态的框架,本文提出一类d⊗d上广义正交两体态基于单向LOCC的区分算法,并主要研究了4⊗4上的可分态,得到了一种快速且有效判断纠缠态是否可单向LOCC区分的算法。但对于dimT⊥=d+t的情况,还有许多与MAS相关的规律需要发现,因此,后期将继续探索其他维上纠缠态的区分规律,例如量子密码、量子秘密共享、量子信道的经典容量、量子纠缠的鲁棒性以及束缚纠缠态等。 [1] GHOSH S,KAR G,ROY A,et al.Distinguishability of Bell States[J].Physical Review Letters,2001,87(27):277902. [2] 杨小东,高国娟,周其旭,等.基于代理重签名的电子政务数据安全交换方案[J].计算机工程,2017,43(2):183-188. [3] RAHAMAN R,PARKER M G.Quantum Scheme for Secret Sharing Based on Local Distinguishability[J].Physical Review A,2015,91(2). [4] 姜 伟.正交量子态的局域区分问题[D].合肥:中国科学技术大学,2009. [5] CHEGLES A.Condition Unambiguous State Distinction Using LOCC[J].Physical Review A,2003,69(5):521-524. [6] HORODECKI M,DE S A,SEN U.Local Distinguishability:More Nonlocality with Less Entanglement[J].Physical Review Letters,2003,90(4):047902. [7] ZHANG Z C,WEN Q Y,GAO F.One-way LOCC Indistinguishability of Naximally Entangled States[J].Quantum Information Processing,2014,13:795-804. [8] FAN H.Distinguishability and Indistinguishability by Local Operations and Classical Communication[J].Physical Review Letters,2004,92(17):177905. [9] HAYASHI M,MARJHAM D,MURAO M,et al.Bounds on Multipartite Orthogonal State Discrimination Using Local Operations and Classical Communication[J].Physical Review Letters,2006,96(4):040501. [10] BENNETT C H,DIVINCENZO D P,MOR T,et al.Unextendible Product Bases and Bound Entanglement[J].Physical Review Letters,1999,82:5385-5488. [11] WAGATE J,HARDY L.Nonlocality,Asymmetry and Distinguishing Bipartite States[J].Physical Review Letters,2002,89(14):147901. [12] BADZIAG P,HORODECKI M,DE S A,et al.Locally Accessible Information:How Much Can the Parties Gain by Cooperating[J].Physical Review Letters,2003,91:117901. [13] COHEN S M.Almost Every Set ofN≥d+1 Ortho-gonal States ond⊗nis Locally Indistinguishable [J].Physical Review A,2008,77:060309. [14] TANMAY S.Framework for Distinguishability of Orthogonal Bipartite States by One-way Local Operations and Classical Communication[J].Physical Review A,2016,93(3):757-758. [15] NATHANSON M.Distinguishing Bipartite Orthogonal States by LOCC:Best and Worst Cases[J].Journal of Mathematical Physics,2005,46(6):901-933.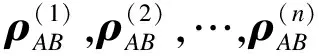
2 d⊗d上的纠缠态区分算法
2.1 纠缠态区分算法内容
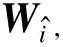
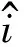
2.2 纠缠态区分算法分析
3 4 ⊗ 4上的纠缠态快速区分算法
3.1 算法原理

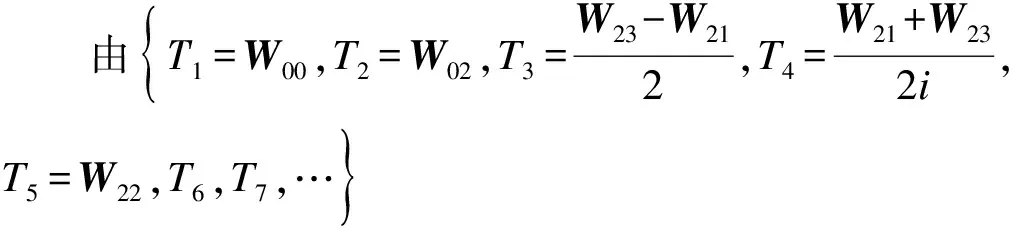
3.2 快速算法内容
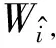
3.3 算法分析

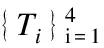

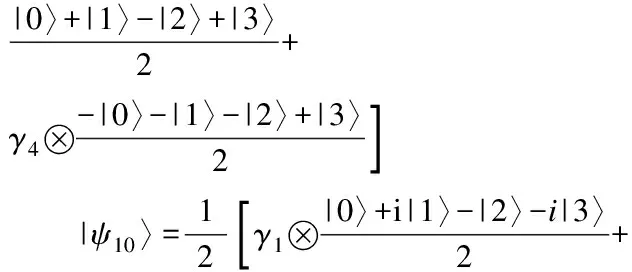
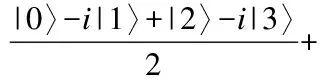
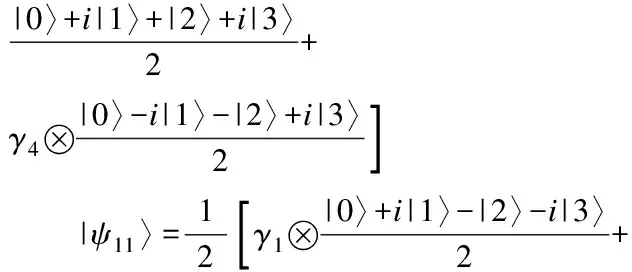
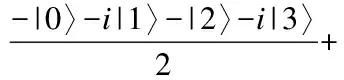
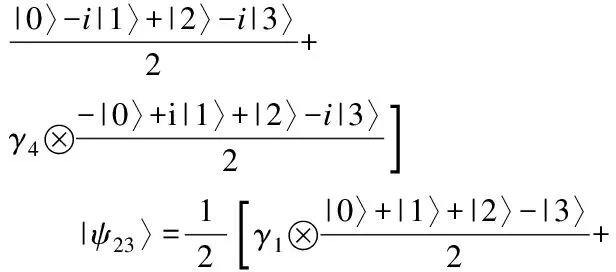

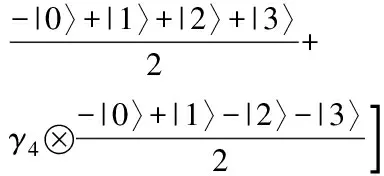
4 结束语
